5.1: Interacciones conservadoras
- Page ID
- 128195
Permítanme resumir los conceptos y principios físicos que hemos encontrado hasta ahora en nuestro estudio de la mecánica clásica. Hemos “descubierto” una cantidad importante, la inercia o masa inercial de un objeto, e introducido dos cantidades diferentes a partir de ese concepto, el impulso\(m \vec v\) y la energía cinética\(\frac{1}{2}mv^2\). Encontramos que estas cantidades tienen propiedades diferentes pero igualmente intrigantes. El impulso total de un sistema es insensible a las interacciones entre las partes que conforman el sistema, y por lo tanto se mantiene constante en ausencia de influencias externas (una declaración más general de la ley de inercia, el primer principio importante que encontramos). La energía cinética total, por otro lado, cambia mientras se produce cualquier tipo de interacción, pero en algunos casos puede volver a su valor original después.
En este capítulo, continuaremos explorando este comportamiento intrigante de la energía cinética, y lo usaremos para obtener algunas ideas importantes sobre los tipos de interacciones que encontramos en la física clásica. En el próximo capítulo, por otro lado, volveremos a la perspectiva de impulso y la utilizaremos para introducir formalmente el concepto de fuerza. De ahí que podamos decir que este capítulo trata sobre las interacciones desde el punto de vista energético, mientras que el próximo capítulo tratará de ellas desde el punto de vista de la fuerza.
En el capítulo anterior sugerí que lo que sucedía en una colisión elástica podría interpretarse, o describirse (quizás de manera figurativa) más o menos de la siguiente manera: a medida que los objetos se juntan, la energía cinética total baja, pero es como si estuviera temporalmente almacenada en alguna parte, y como la los objetos se separan, esa “energía almacenada” se recupera completamente como energía cinética. Si esto sucede o no en alguna colisión en particular (es decir, si la colisión es elástica o no) depende, como hemos visto, del tipo de interacción (“hinchable” o “pegajosa”, por ejemplo) que tenga lugar entre los objetos.
Vamos a tomar la descripción anterior literalmente, y usar el nombre de interacción conservadora para cualquier interacción que pueda “almacenar y restaurar” la energía cinética de esta manera. A la propia “energía almacenada” —que en realidad no es energía cinética mientras permanece almacenada, ya que no viene dada por el valor de\(\frac{1}{2}mv^2\) en ese momento— vamos a llamar energía potencial. Así, las interacciones conservadoras serán aquellas que tengan una “energía potencial” asociada a ellas, y viceversa.
Energía Potencial
Quizás el ejemplo más simple y claro del almacenamiento y recuperación de la energía cinética es lo que sucede cuando arrojas un objeto recto hacia arriba, ya que sube y eventualmente vuelve a caer. El objeto deja tu mano con algo de energía cinética; a medida que sube se ralentiza, por lo que su energía cinética baja, baja... todo el camino hasta cero, eventualmente, ya que momentáneamente se detiene en la parte superior de su ascenso. Luego baja, y su energía cinética comienza a aumentar de nuevo, hasta que finalmente, como vuelve a tu mano, tiene casi la misma energía cinética con la que empezó (exactamente la misma, en realidad, si descuidas la resistencia al aire).
La interacción responsable de este cambio en la energía cinética del objeto es, por supuesto, la interacción gravitacional entre éste y la Tierra, por lo que vamos a decir que la energía cinética “faltante” se almacena temporalmente como energía potencial gravitacional del sistema formado por la Tierra y el objeto.
Incluso tenemos una manera de describir matemáticamente lo que está pasando. Recordemos la ecuación\(v^2_f − v^2_i = 2a \Delta x\) para el movimiento bajo aceleración constante. Usemos\(y\) en lugar de\(x\), para el movimiento vertical; dejemos\(a = −g\), y dejemos que\(v_f\) solo sea la velocidad genérica\(v\),, a alguna altura arbitraria\(y\). Tenemos
\[ v^{2}-v_{i}^{2}=-2 g\left(y-y_{i}\right) \nonumber .\]
Ahora multiplique ambos lados de esta ecuación por\(\frac{1}{2}m\):
\[ \frac{1}{2} m v^{2}-\frac{1}{2} m v_{i}^{2}=-m g\left(y-y_{i}\right) \label{eq:5.1} \]
El lado izquierdo de (\ ref {eq:5.1}) es solo el cambio en la energía cinética (desde su valor inicial cuando se lanzó el objeto). Interpretaremos el lado derecho como el negativo del cambio en la energía potencial gravitacional. Para que esto sea más claro, reorganice la Ecuación (\ ref {eq:5.1}) moviendo todas las cantidades “iniciales” a un lado:
\[ \frac{1}{2} m v^{2}+m g y=\frac{1}{2} m v_{i}^{2}+m g y_{i} \label{eq:5.2} .\]
Vemos, entonces, que la cantidad\(\frac{1}{2}mv^2 + mgy\) permanece constante (siempre igual a su valor inicial) a medida que el objeto sube y baja. Definamos la energía potencial gravitacional de un sistema formado por la Tierra y un objeto a una altura por\(y\) encima de la superficie de la Tierra como la siguiente función simple de\(y\):
\[ U^{G}(y)=m g y \label{eq:5.3} .\]
Entonces vemos de la Ecuación (\ ref {eq:5.2}) que
\[ K + U^G = \mathrm{constant} \label{eq:5.4} .\]
Esta es una declaración de conservación de la energía bajo la interacción gravitacional. Para cualquier interacción que tenga asociada una energía potencial, la cantidad\(K + U\) se denomina energía mecánica (total).
La figura\(\PageIndex{1}\) muestra cómo las energías cinéticas y potenciales de un objeto arrojado hacia arriba cambian con el tiempo. Para calcular\(K\) he usado la ecuación\(v = v_i − gt\) (tomando\(t_i\) = 0); para calcular\(U^G = mgy\), he usado\(y = y_i + v_it − \frac{1}{2}gt^2\). Yo he asumido arbitrariamente que el objeto tiene una masa de 1 kg y una velocidad inicial de 2 m/s, y es arrojado desde una altura inicial de 0.5 m sobre el suelo. Observe cómo el cambio en la energía potencial refleja exactamente el cambio en la energía cinética (así\(\Delta U^G = −\Delta K\), como lo indica la Ecuación (\ ref {eq:5.1})), y la energía mecánica total permanece igual a su valor inicial de 6.9 J en todo momento.
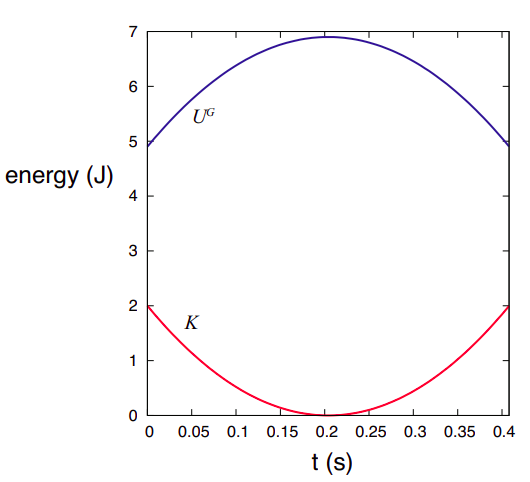
Hay algo sobre la energía potencial que probablemente deba mencionarse en este momento. Porque he optado por lanzar el objeto desde 0.5 m sobre el suelo, y he optado por medir\(y\) desde el suelo, comencé con una energía potencial de\(mgy_i\) = 4.9 J. Esto tiene sentido, en cierto modo: te dice que si simplemente dejaste caer el objeto desde esta altura, habría recogido una cantidad de energía cinética igual a 4.9 J en el momento en que llegó al suelo. Pero, en realidad, donde elijo el origen vertical de las coordenadas es arbitrario. Podría comenzar a medir\(y\) desde cualquier altura que quisiera, por ejemplo, tomando la altura inicial de mi mano para corresponder a\(y\) = 0. Esto desplazaría la curva azul en la Figura\(\PageIndex{1}\) hacia abajo en 4.9 J, pero no cambiaría ninguna de las físicas. Lo único importante para lo que realmente quiero la energía potencial es para calcular la energía cinética que el objeto perderá o ganará a medida que se mueve de una altura a otra, y para eso solo cambios en materia energética potencial. Siempre puedo sumar o restar cualquier número (constante) 1 a o desde\(U\), y seguirá siendo cierto que\(\Delta K = −\Delta U\).
¿Qué pasa con la energía potencial en el contexto en el que la encontramos por primera vez, el de las colisiones elásticas en una dimensión? Imagínese que tenemos dos carros chocan en una pista de aire, y uno de ellos, digamos el carro 2, está equipado con un resorte. A medida que los carros se unen, comprimen el resorte, y parte de su energía cinética se “almacena” en él como energía potencial elástica. En física, utilizamos la siguiente expresión para la energía potencial almacenada en lo que llamamos un resorte ideal 2:
\[ U^{\operatorname{spr}}(x)=\frac{1}{2} k\left(x-x_{0}\right)^{2} \label{eq:5.5} \]
donde\(k\) es algo llamado constante de resorte;\(x_0\) es la “longitud de equilibrio” del resorte (cuando no está comprimido ni estirado); y\(x\) su longitud real, por lo que\(x>x_0\) significa que el resorte está estirado, y\(x<x_0\) significa que está comprimido. Para el sistema de los dos carros colisionando, podemos tomar la energía potencial a dar por la Ecuación (\ ref {eq:5.5}) si la distancia entre los carros es menor que\(x_0\), y 0 (correspondiente a un resorte relajado) en caso contrario. Si ponemos el carro 1 a la izquierda y el carro 2 a la derecha, entonces la distancia entre ellos es\(x_2 − x_1\), y así podemos escribir, para toda la interacción
Esto es suficiente para resolver el movimiento de los dos carros, dadas las condiciones iniciales. Para ver cómo, mira en la sección “Ejemplos” al final de este capítulo. Aquí, sólo te voy a dar el resultado.
Para el cálculo, que se muestra en la Figura\(\PageIndex{2}\) siguiente, he elegido el carro 1 para tener una masa de 1 kg, una posición inicial (at\(t\) = 0) de\(x_{1i}\) = −5 cm y una velocidad inicial de 1 m/s, mientras que el carro 2 tiene una masa de 2 kg y comienza en reposo en\(x_{2i}\) = 0. He asumido que el resorte tiene una longitud de\(x_0\) = 2 cm y una constante de resorte\(k\) = 1000 J/m 2 (que suena como mucho pero no lo es realmente). La colisión comienza en\(t_c = (x_{2i} − x_0 − x_{1i})/v_{1i}\) = 0.03 s, que es el tiempo que tarda el carro 1 en recorrer los 3 cm separándolo del extremo del muelle. Previo a ese punto, la energía cinética total\(K_{sys}\) = 0.5 J, y la energía potencial total\(U\) = 0.
Como resultado de la colisión, el resorte comprime y sufre “medio ciclo” de oscilación con una “frecuencia angular”\(\omega = \sqrt{k/ \mu} \) (donde\(\mu\) está, como en capítulos anteriores, la “masa reducida” del sistema,\(\mu = m_1m_2/(m_1 + m_2)\)). Es decir, el resorte se comprime y luego empuja hacia afuera hasta que vuelve a su longitud de equilibrio 3. Esto dura desde\(t = t_c\) hasta\(t = t_c + \pi / \omega\), tiempo durante el cual las energías potenciales y cinéticas del sistema pueden escribirse como
(no te preocupes, todo esto va a tener mucho más sentido después de que lleguemos al Capítulo 11 sobre movimiento armónico simple, ¡lo prometo!). Después\(t = t_c + \pi / \omega\), la interacción ha terminado,\(K\) y\(U\) volver a sus valores iniciales.
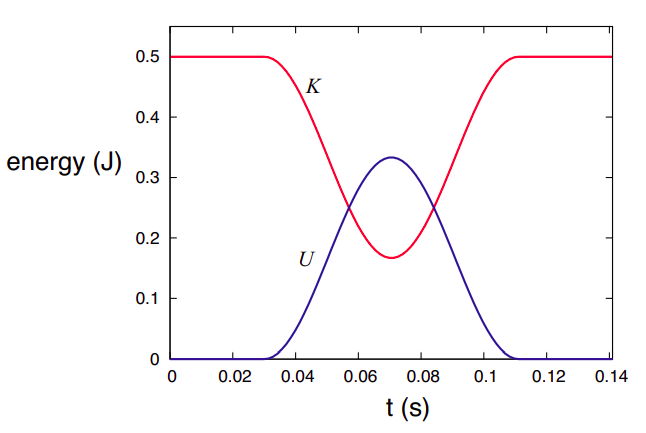
Si compara la Figura\(\PageIndex{2}\) con la Figura 4.2.1 del Capítulo 4, verá que la curva de energía cinética se ve muy similar, a excepción de la escala de tiempo, que aquí es centésimas de segundo y allá se tomó para ser milisegundos. La cantidad que determina la escala de tiempo aquí es el “medio periodo” de oscilación,\(\pi / \omega = \pi \sqrt{\mu /k}\) = 0.081 s para los valores de\(k\) y\(\mu\) asumidos aquí. Podríamos hacer esto más pequeño haciendo que el resorte sea más rígido (aumentando\(k\)), o los bloques más ligeros (reduciendo µ), pero no tiene mucho sentido intentarlo, ya que las colisiones en los Capítulos 3 y 4 fueron todas simplemente maquilladas en cualquier caso.
El punto principal es que este tipo de configuración física (un carro equipado con un resorte) nos daría de hecho una colisión elástica, y una curva de energía cinética muy parecida a las que utilicé, con fines ilustrativos, en el Capítulo 4; solo que ahora también tenemos una curva de energía potencial para ir con ella, y para mostrar dónde está la energía se “esconde” mientras dure la colisión.
(Podría preguntarse, de todos modos, ¿qué tipo de función de energía potencial produciría realmente las curvas de colisión elásticas inventadas en los capítulos 3 y 4? La respuesta (quizás sorprendente) es, realmente no lo sé, ¡y no tengo forma de averiguarlo! Si tienes curiosidad sobre por qué, vuelve a mirar la sección “Ejemplos” al final del capítulo).
1 Por supuesto, algunas opciones pueden resultar en que la energía potencial, e incluso la energía total, ¡a veces sea negativa! Si esta noción de una energía total negativa te molesta un poco, espera hasta el capítulo sobre la gravedad (Capítulo 10), donde trataremos de darle algún sentido...
2 Un “resorte ideal” se define básicamente, matemáticamente, por esta expresión, o por la ecuación de fuerza correspondiente (6.2.10) (que estudiaremos en el siguiente capítulo, y que se conoce con el nombre de la ley de Hooke); generalmente, también requerimos que el resorte sea “sin masa” (por lo que queremos decir que su masa debe ser insignificante en comparación con todas las demás masas involucradas en cualquier problema dado). Por supuesto, para que la Ecuación (\ ref {eq:5.5}) sostenga\(x < x_0\), debe ser posible comprimir el resorte así como estirarlo, lo que no siempre es posible con algunos resortes.
3 Como se señaló anteriormente, siempre asumiremos que nuestros manantiales son “sin masa”, es decir, que su inercia es despreciable. A su vez, una inercia insignificante significa que el resorte no “sigue adelante”: deja de estirarse en cuanto vuelve a su longitud original.
Funciones Energéticas Potenciales y “Paisajes Energéticos”
La función de energía potencial de un sistema, como se ilustra en los ejemplos anteriores, sirve para hacernos saber cuánta energía se puede almacenar en, o extraer de, el sistema cambiando su configuración, es decir, las posiciones de sus partes relativas entre sí. Esto lo hemos visto en el caso de la fuerza gravitacional (siendo la “configuración” en este caso la distancia entre el objeto y la tierra), y justo ahora en el caso de un resorte (qué tan estirado o comprimido está). En todos estos casos debemos pensar en la energía potencial como una propiedad del sistema en su conjunto, no una parte individual; es, hablando muy vagamente, algo parecido a un “estrés” en el sistema que se puede convertir en movimiento en las condiciones adecuadas.
Es consecuencia del principio de conservación del impulso que, si la interacción entre dos partículas puede ser descrita por una función energética potencial, ésta debe ser función únicamente de su posición relativa, es decir, la cantidad\(x_1 − x_2\) (o\(x_2 − x_1\)), y no de las coordenadas individuales, \(x_1\)y\(x_2\), por separado 4. El ejemplo del resorte en la sección anterior ilustra esto, mientras que el ejemplo de energía potencial gravitacional muestra cómo esto puede simplificarse en un caso importante: en la Ecuación (\ ref {eq:5.3}), la altura\(y\) del objeto sobre el suelo es realmente una medida de la distancia entre el objeto y la tierra, algo que podríamos escribir, en plena generalidad, como\(|\vec r_o − \vec r_E|\) (dónde\(\vec r_o\) y\(\vec r_E\) son los vectores de posición de la Tierra y del objeto, respectivamente). Sin embargo, como no esperamos que la Tierra se mueva mucho como resultado de la interacción, podemos tomar su posición como constante, y sólo incluir la posición del objeto explícitamente en nuestra función energética potencial, como hicimos arriba 5.
En términos generales, entonces, podemos identificar una gran clase de problemas donde un objeto “pequeño” o “partícula” interactúa con uno mucho más masivo, y es una buena aproximación para escribir la energía potencial de todo el sistema en función únicamente de la posición de la partícula. En una dimensión, entonces, tenemos una situación en la que, una vez conocidas las condiciones iniciales (la posición inicial de la partícula y la velocidad), el movimiento de la partícula puede determinarse completamente a partir de la función\(U(x)\), donde\(x\) está la posición de la partícula en un momento dado. Esto se puede hacer usando cálculo (es decir, dejar\(v=\pm \sqrt{2 m(E-U(x))}\) y resolver la ecuación diferencial resultante); pero también es posible obtener algunas ideas bastante valiosas sobre el movimiento de la partícula sin usar ningún cálculo en absoluto, a través de un enfoque mayormente gráfico que me gustaría mostrarles a continuación.
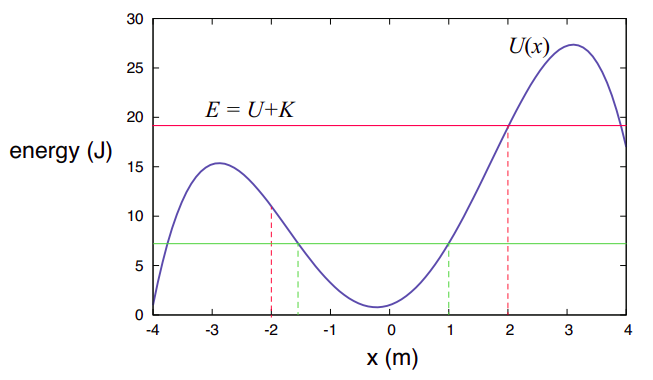
En la Figura\(\PageIndex{3}\) anterior he asumido, como ejemplo, que la energía potencial del sistema, en función de la posición de la partícula, viene dada por la función\(U(x) = −x^4/4+9x^2/2+2x + 1\) (en julios, si\(x\) se da en metros). Consideremos entonces qué sucede si la partícula tiene una masa\(m\) = 4 kg y se encuentra inicialmente a\(x_i\) = −2 m, con una velocidad\(v_i\) = 2 m/s. (Este escenario va con las líneas rojas en la Figura\(\PageIndex{3}\), así que por favor ignore las líneas verdes por el momento.) Su energía cinética será entonces\(K_i\) = 8 J, mientras que la energía potencial será\(U(−2)\) = 11 J. La energía mecánica total es entonces\(E\) = 19 J, como lo indica la línea horizontal roja.
Ahora, a medida que la partícula se mueve, la energía total se mantiene constante, así que a medida que se mueve hacia la derecha, su energía potencial baja al principio, y en consecuencia su energía cinética sube, es decir, acelera. En algún momento, sin embargo (alrededor\(x\) = −0.22 m) la energía potencial comienza a subir, y así la partícula comienza a disminuir la velocidad, aunque sigue funcionando, porque\(K = E − U\) sigue siendo distinta de cero. Sin embargo, cuando la partícula finalmente alcanza el punto\(x\) = 2 m, la energía potencial\(U(2)\) = 19 J, y la energía cinética se vuelve cero.
En ese punto, la partícula se detiene y da la vuelta, al igual que un objeto arrojado verticalmente hacia arriba. A medida que se mueve “por la colina de energía potencial”, recupera la energía cinética que solía tener, de manera que cuando vuelve a alcanzar el punto de partida\(x\) = −2 m, su velocidad vuelve a ser de 2 m/s, pero ahora se mueve en sentido contrario, por lo que simplemente pasa por y sobre el siguiente “cerro” (ya que tiene suficiente total energía para hacerlo), y eventualmente se mueve fuera de la región que se muestra en la figura.
Como otro ejemplo, considere lo que hubiera ocurrido si la partícula hubiera sido liberada a, digamos,\(x\) = 1 m, pero con velocidad cero. (Esto se ilustra por las líneas verdes en la Figura\(\PageIndex{3}\).) Entonces la energía total sería solo la energía potencial\(U(1)\) = 7.25 J. La partícula no podría posiblemente moverse hacia la derecha, ya que eso requeriría que la energía total suba. Sólo puede moverse hacia la izquierda, ya que en esa dirección\(U(x)\) disminuye (inicialmente, al principio), y eso significa que\(K\) puede aumentar (la memoria siempre\(K\) es positiva siempre y cuando la partícula esté en movimiento). Entonces la partícula se acelera hacia la izquierda hasta que, más allá del punto\(x\) = −0.22 m,\(U(x)\) comienza a aumentar de nuevo y\(K\) tiene que bajar. Finalmente, como muestra la figura, llegamos a un punto (que podemos calcular para ser\(x\) = −1.548 m) donde una vez más\(U(x)\) es igual a 7.25 J. Esto no deja espacio para ninguna energía cinética, por lo que la partícula tiene que detenerse y volver atrás. El movimiento resultante consiste en que la partícula oscila de un lado a otro para siempre entre\(x\) = −1.548 m y\(x\) = 1 m.
En este punto, es posible que hayas notado que el movimiento que he descrito como siguiente de la\(U(x)\) función en Figura\(\PageIndex{3}\) se asemeja mucho al movimiento de un automóvil en una montaña rusa que tiene la forma mostrada, o tal vez una bola rodando arriba y abajo colinas como las que se muestran en la imagen. De hecho, la correspondencia se puede hacer exacta, si sustituimos el deslizamiento por el balanceo, ya que el movimiento rodante tiene complicaciones propias. Dada una función arbitraria de energía potencial\(U(x)\) para una partícula de masa\(m\), imagina que construyes un “paisaje” de cerros y valles cuya altura\(y\) por encima de la horizontal, para un valor dado de la coordenada horizontal\(x\), viene dada por la función\(y(x) = U(x)/mg\). (Tenga en cuenta que\(mg\) es solo un factor de escala constante que no cambia la forma de la curva). Entonces, para un objeto de masa que se\(m\) deslice sin fricción sobre ese paisaje, bajo la influencia de la gravedad, la energía potencial gravitacional en cualquier punto\(x\) sería\(U^G(x) = mgy = U(x)\), y por lo tanto su velocidad en cualquier punto será precisamente la misma que la de la partícula original, si inicia en el mismo punto con la misma velocidad
Esta noción de “paisaje energético” puede extenderse a más de una dimensión (¡aunque son difíciles de visualizar en tres!) , o generalizado para tratar con parámetros de configuración distintos de la posición de una sola partícula. Puede ser muy útil en una serie de disciplinas (no solo la física), para predecir las formas en que la configuración de un sistema puede ser probable que cambie.
4 ¡Veremos por qué en el próximo capítulo! Pero, si quieres echar un vistazo adelante, nada te impide leer ahora mismo las secciones 6.1 y 6.2. Básicamente, para conservar el impulso necesitamos la Ecuación (6.1.6) para mantener, y como se puede ver en la Ecuación (6.2.7), tener la energía potencial depender sólo de eso lo\(x_1 − x_2\) asegura.
5 Esto cambiará en el Capítulo 10, cuando lleguemos a estudiar la gravedad sobre una escala planetaria.