7.3: El “Centro de Trabajo Masivo”

Última actualización
Guardar como PDF

Page ID: 128418

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Toda la física que utilicé para derivar el resultado (7.2.8) fue\(F = ma\), y la expresión\(v^2_f −v^2_i = 2a\Delta x\), que se aplica siempre que tengamos movimiento con aceleración constante. Ahora bien, sabemos que para un sistema arbitrario, de masa total\(M\),\(F_{ext,net} = M a_{cm}\) [ver Ecuación (6.1.11)]. Eso es suficiente, entonces, para asegurar que, si\(F_{ext,net}\) es una constante, vamos a tener

\[ F_{\text {ext,net}} \Delta x_{c m}=\Delta K_{c m} \label{eq:7.12} \]

donde\(K_{cm}\), la energía cinética traslacional, es, como de costumbre\(K_{cm} = \frac{1}{2}Mv^2_{cm}\),, y\(\Delta x_{cm}\) es el desplazamiento del centro de masa. El resultado (\ ref {eq:7.12}) se mantiene para un sistema arbitrario, siempre y cuando\(F_{ext,net}\) sea constante, y puede generalizarse por medio de una integral (como en la Ecuación (7.2.6)) cuando es variable.

Entonces parece que podríamos definir el lado izquierdo de la Ecuación (\ ref {eq:7.12}) como “el trabajo realizado en el centro de masa”, y tomar eso como la generalización natural a un sistema del resultado (7.2.8) para una partícula. La mayoría de los físicos, de hecho, estarían bien con eso, pero los educadores hoy en día fruncen el ceño ante esa idea, por un par de razones.

En primer lugar, parece que es esencial para la noción de trabajo que se debe multiplicar la fuerza por el desplazamiento del objeto sobre el que está actuando. Más precisamente, en la definición (7.2.1), queremos el desplazamiento del punto de aplicación de la fuerza ¹. Pero hay muchos ejemplos de sistemas donde no hay nada en la ubicación precisa del centro de masas, y ciertamente ninguna fuerza que actúe precisamente ahí.

Esto no es necesariamente un problema en el caso de un objeto rígido que no está haciendo nada gracioso, simplemente moviéndose como un todo para que cada parte tenga el mismo desplazamiento, porque entonces el desplazamiento del centro de masa simplemente representaría el desplazamiento de cualquier punto en el que una fuerza externa pudiera realmente ser aplicado. Pero para muchos sistemas deformables, este no sería el caso. De hecho, para tales sistemas generalmente se puede demostrar que en realidad no\(F_{ext,net} \Delta x_{cm} \) es el trabajo realizado en el sistema por la fuerza externa neta. Un ejemplo sencillo de dicho sistema se muestra a continuación, en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un sistema de dos bloques conectados por un muelle. Se aplica una fuerza externa constante\(\vec F^c_{h,2}\),, al bloque de la derecha. Inicialmente el resorte está relajado, pero en cuanto el bloque 2 comienza a moverse se estira, tirando hacia atrás en el bloque 2 y tirando hacia adelante en el bloque 1. Debido al estiramiento de la primavera, los desplazamientos\(\Delta x_1\),\(\Delta x_{cm}\) y todos\(\Delta x_2\) son diferentes, y el trabajo realizado por la fuerza externa,\(F^c_{h,2} \Delta x_2\), es diferente del “centro de trabajo masivo”\(F^c_{h,2} \Delta x_{cm}\).

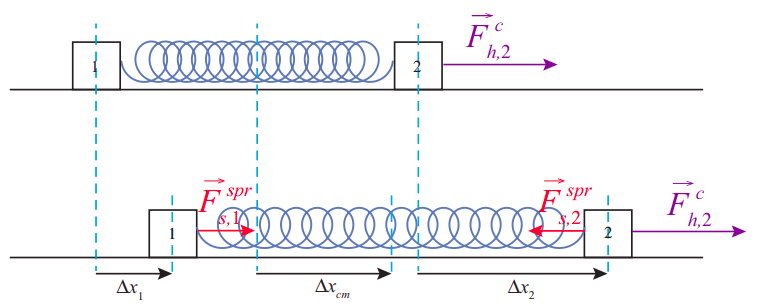
En esta figura, los dos bloques están conectados por un resorte, y la fuerza externa se aplica al bloque de la derecha (bloque 2). Si los bloques tienen la misma masa, el centro de masa del sistema es un punto exactamente a medio camino entre ellos. Si la primavera inicia en su estado relajado, se estirará al principio, de manera que el centro de masa se quede rezagado con respecto al bloque 2\(F^c_{h,2} \Delta x_2\), y, que es la cantidad que deberíamos llamar propiamente el “trabajo realizado por la fuerza externa neta” no será igual a la\(F^c_{h,2} \Delta x_{cm}\).

Nos encontramos, por tanto, con un resultado muy general y potencialmente bastante útil, Ecuación (\ ref {eq:7.12}), que se parece mucho a que debería ser “el trabajo realizado en el sistema por la fuerza externa neta” pero, de hecho, es que sólo a veces. Por otro lado, el resultado es tan útil que simplemente referirse a él todo el tiempo por “Ecuación (\ ref {eq:7.12})” no servirá. Propongo, por lo tanto, llamarlo el “centro del trabajo masivo”, entre comillas, solo para que todos sepamos de lo que estamos hablando, y recordemos las advertencias que conlleva.

Ahora podemos pasar al teorema real relacionando el trabajo de las fuerzas externas sobre un sistema con el cambio en su energía. Lo que hemos visto hasta ahora son en realidad solo aplicaciones sencillas de la segunda ley de Newton. El principal resultado que viene es más profundo que eso, ya que implica también, en última instancia, el principio de conservación de la energía.

¹ Como su nombre lo indica, este es el punto preciso en el que se aplica la fuerza. Para las fuerzas de contacto (distintas a la fricción; ver más adelante), esto se identifica fácilmente. Para la gravedad, se puede demostrar que una suma sobre todas las fuerzas ejercidas sobre todas las partículas que componen el objeto es equivalente a una sola fuerza resultante que actúa en un punto llamado centro de gravedad, que, para nuestros fines (objetos en campos gravitacionales uniformes o casi uniformes) será lo mismo que el centro de masa.