7.4: Trabajo realizado en un sistema por todas las fuerzas externas
- Page ID
- 128393
Consideremos el sistema más general posible, uno que pudiera contener cualquier número de partículas, con posiblemente muchas fuerzas, tanto internas como externas, actuando sobre cada una de ellas. Nuevamente, por simplicidad, comenzaré por considerar lo que sucede en un intervalo de tiempo tan corto que todas las fuerzas son aproximadamente constantes (el resultado final se mantendrá durante intervalos de tiempo arbitrariamente largos, simplemente agregando, o integrando, en muchos intervalos tan cortos). También trabajaré explícitamente solo el caso unidimensional, aunque de nuevo eso resulta no ser una restricción real.
\(W_{all,1}\)Sea entonces el trabajo realizado sobre la partícula 1 por todas las fuerzas que actúan sobre ella,\(W_{all,2}\) el trabajo realizado sobre la partícula 2, y así sucesivamente. El trabajo total es la suma\(W_{all,sys} = W_{all,1} + W_{all,2} + \cdots\). Sin embargo, por los resultados de la sección 7.2, tenemos\(W_{all,1} = \Delta K_1\) (el cambio en la energía cinética de la partícula 1)\(W_{all,2} = \Delta K_2\), y así sucesivamente, así que sumando todos estos obtenemos
\[ W_{a l l, s y s}=\Delta K_{s y s} \label{eq:7.13} \]
donde\(\Delta K_{sys}\) está el cambio en la energía cinética de todo el sistema.
Hasta el momento, claro, esto no es nada nuevo. Para aprender algo más necesitamos mirar a continuación el trabajo realizado por las fuerzas internas. Aquí es útil comenzar considerando el “caso de no disipación” en el que todas las fuerzas internas pueden derivarse de una energía potencial 2. Consideraremos el caso donde los procesos disipativos ocurren dentro del sistema después de haber adquirido una comprensión completa del resultado que obtendremos para este caso más simple.
2 O de lo contrario no hacen ningún trabajo: la fuerza magnética entre cargas móviles es un ejemplo de estas últimas.
El caso sin disipación
Las fuerzas internas son, por definición, fuerzas que surgen de las interacciones entre pares de partículas que están ambas dentro del sistema. Debido a la tercera ley de Newton, la fuerza\(F_{12}\) (omitiremos el superíndice “tipo” por ahora) ejercida por la partícula 1 sobre la partícula 2 debe ser la negativa de\(F_{21}\), la fuerza ejercida por la partícula 2 sobre la partícula 1. De ahí que se pueda escribir el trabajo asociado a esta interacción para este par de partículas
\[ W(1,2)=F_{12} \Delta x_{2}+F_{21} \Delta x_{1}=F_{12}\left(\Delta x_{2}-\Delta x_{1}\right) \label{eq:7.14} .\]
Observe que se\(\Delta x_2 − \Delta x_1\) puede reescribir como\(x_{2, f}-x_{2, i}-x_{1, f}+x_{1, i}=x_{12, f}-x_{12, i}=\Delta x_{12} \), donde\(x_{12} = x_2 − x_1\) está la coordenada de posición relativa de las dos partículas. Por lo tanto,
\[ W(1,2)=F_{12} \Delta x_{12} \label{eq:7.15} .\]
Ahora bien, si la interacción en cuestión se asocia con una energía potencial, como mostré en la sección 6.2,\(F_{12} = −dU/dx_{12}\). Supongamos que el desplazamiento\(\Delta x_{12}\) es tan pequeño que podemos reemplazar la derivada por solo la relación\(\Delta U/ \Delta x_{12}\) (lo cual es consistente con nuestra suposición de que la fuerza es aproximadamente constante en el intervalo de tiempo considerado); el resultado será entonces
\[ W(1,2)=F_{12} \Delta x_{12} \simeq-\frac{\Delta U}{\Delta x_{12}} \Delta x_{12}=-\Delta U \label{eq:7.16} .\]
Sumando muchos de esos desplazamientos “infinitesimales” conducirá al mismo resultado final, donde\(\Delta U\) estará el cambio en la energía potencial a lo largo de todo el proceso. Esto también se puede probar usando cálculo, sin ninguna aproximación:
\[ W(1,2)=\int_{x_{12, i}}^{x_{12, f}} F_{12} d x_{12}=-\int_{x_{12, i}}^{x_{12, f}} \frac{d U}{d x_{12}} d x_{12}=-\Delta U \label{eq:7.17} .\]
Podemos aplicar esto a cada par de partículas y cada interacción interna, y luego sumar todos los resultados. Por un lado, obtendremos el trabajo total realizado en el sistema por todas las fuerzas internas; por otro lado, obtendremos lo negativo del cambio en la energía interna total del sistema:
\[ W_{i n t, s y s}=-\Delta U_{s y s} \label{eq:7.18} .\]
En palabras, el trabajo realizado por todas las fuerzas internas (conservadoras) es igual al cambio en la energía potencial del sistema.
Pongamos ahora las Eqs. (\ ref {eq:7.13}) y (\ ref {eq:7.18}) juntos: la diferencia entre el trabajo realizado por todas las fuerzas y el trabajo realizado por las fuerzas internas es, por supuesto, el trabajo realizado por las fuerzas externas, pero de acuerdo con las Eqs. (\ ref {eq:7.13}) y (\ ref {eq:7.18}), esto es igual a
\[ W_{e x t, s y s}=W_{a l l, s y s}-W_{i n t, s y s}=\Delta K_{s y s}+\Delta U_{s y s} \label{eq:7.19} \]
que es el cambio en la energía mecánica total (cinética más potencial) del sistema. Si asumimos además que el sistema, en ausencia de las fuerzas externas, está cerrado, entonces no hay otros procesos (como la absorción de calor) por los cuales la energía total del sistema pueda cambiar, y obtenemos el resultado simple de que el trabajo realizado por las fuerzas externas equivale al cambio en el energía total del sistema:
\[ W_{e x t, s y s}=\Delta E_{s y s} \label{eq:7.20} .\]
Como primera aplicación del resultado (\ ref {eq:7.20}), considere nuevamente los bloques conectados por un resorte que se muestra en la Figura 7.3.1. Se puede ver ahora por qué el trabajo realizado por la fuerza externa\(F^c_{h,2}\) tiene que ser diferente, y de hecho más grande, que el “centro de trabajo masivo”: este último sólo nos da el cambio en la energía traslacional, pero el primero tiene que darnos el cambio en la energía total—traslacional, convertible, y potencial:
\ begin {align}
F_ {h, 2} ^ {c}\ Delta x_ {c m} &=\ Delta K_ {c m}\ nonumber\\
F_ {h, 2} ^ {c}\ Delta x_ {2} &=\ Delta K_ {c m} +\ Delta K_ {c o n v} +\ Delta U^ {s p r}\ etiqueta {eq:7.21}.
\ end {align}
Como otro ejemplo, imagina que lanzas una bola de masa\(m\) hacia arriba (ver Figura\(\PageIndex{1}\)), y alcanza una altura máxima\(h\) por encima del punto donde tu mano comenzó a moverse. Definamos el sistema para que sea la pelota y la tierra, así la fuerza que ejerce tu mano es una fuerza externa. Entonces haces trabajo en el sistema durante el lanzamiento, que en la figura es el intervalo, de A a B, durante el cual tu mano está en contacto con el balón. El diagrama de barras en el lateral muestra que parte de este trabajo se dedica a aumentar la energía potencial (gravitacional) del sistema (porque la pelota sube un poco mientras está en contacto con tu mano), y el resto, que suele ser la mayor parte, va a aumentar la energía cinética del sistema (en este caso, solo la bola; ¡la energía cinética de la tierra no cambia de ninguna manera medible!).
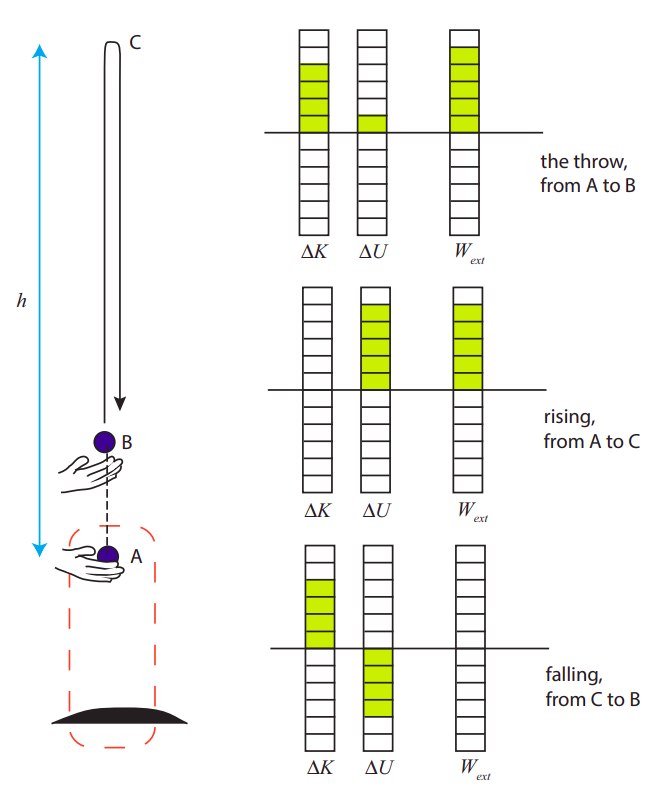
Entonces, ¿cuánto trabajo hiciste realmente? Si conociéramos la distancia de A a B, y la magnitud de la fuerza que ejerciste, y si pudiéramos suponer que tu fuerza fue constante en todo momento, podríamos calcular\(W\) a partir de la definición (7.2.1). Pero en este caso, y a muchos otros les gusta, en realidad es más fácil averiguar cuánta energía total ganó el sistema y simplemente usar Ecuación (\ ref {eq:7.20}). Para encontrar\(\Delta E\) en la práctica, lo único que tenemos que hacer es ver qué tan alto sube la pelota. A la altura máxima de la pelota (punto C), como muestra el segundo diagrama, toda la energía en el sistema es energía potencial gravitacional, y (mientras el sistema permanezca cerrado), toda esa energía sigue siendo igual al trabajo que hiciste inicialmente, así que si la distancia de A a C es\(h\) debes haber hecho una cantidad de trabajo
\[ W_{y o u}=\Delta U^{G}=m g h \label{eq:7.22} .\]
El tercer diagrama de la Figura\(\PageIndex{1}\) muestra el balance trabajo-energía para otro intervalo de tiempo, durante el cual la pelota cae de C a B. Durante este tiempo, ninguna fuerza externa actúa sobre la pelota (recordemos que hemos tomado el sistema para ser la bola y la tierra, por lo que la gravedad es una fuerza interna). Entonces, el trabajo realizado por las fuerzas externas es cero, y el cambio en la energía total del sistema también es cero. El diagrama solo muestra un aumento en la energía cinética a expensas de una disminución igual en la energía potencial.
¿Y el trabajo realizado por las fuerzas internas? La ecuación (\ ref {eq:7.18}) nos dice que este trabajo es igual a lo negativo del cambio en la energía potencial. En este caso, la fuerza interna es la gravedad, y la energía correspondiente es la energía potencial gravitacional. Este cambio en la energía potencial es claramente visible en todos los diagramas; sin embargo, cuando se le agrega el cambio en la energía cinética, el resultado siempre es igual al trabajo realizado por la fuerza externa solamente. Dicho de otra manera, las fuerzas internas no cambian la energía total del sistema, simplemente la “redistribuyen” entre diferentes tipos, como en, por ejemplo, el último diagrama de la Figura\(\PageIndex{1}\), donde se puede ver claramente que la gravedad está haciendo que la energía cinética del sistema aumente a expensas del potencial energía.
Usaremos diagramas como los de la Figura\(\PageIndex{1}\) para observar el balance trabajo-energía para diferentes sistemas. La idea es que la suma de todas las columnas de la izquierda (el cambio en la energía total del sistema) tiene que igualar el resultado en la columna de extrema derecha (el trabajo realizado por la fuerza externa neta): ese es el contenido del teorema (\ ref {eq:7.20}). Tenga en cuenta que, a diferencia de los diagramas de energía que usamos en el Capítulo 5, estas columnas representan cambios en la energía, por lo que podrían ser positivos o negativos.
Al igual que para los diagramas de energía anteriores, la imagen que obtengamos será diferente, incluso para la misma situación física, dependiendo de la elección del sistema. Esto se ilustra en la Figura\(\PageIndex{2}\) a continuación, donde he tomado el mismo lanzamiento que se muestra en la Figura\(\PageIndex{1}\), pero ahora el sistema que estoy viendo es solo el balón. Esto significa que la gravedad es ahora una fuerza externa, al igual que la fuerza de la mano, y la pelota sólo tiene energía cinética. Normalmente se mostraría la suma del trabajo realizado por las dos fuerzas externas en una sola columna, pero aquí he optado por dividirlo en dos columnas para mayor claridad.
Como se puede ver, durante el lanzamiento la mano hace trabajo positivo, mientras que la gravedad hace una cantidad comparativamente pequeña de trabajo negativo, y el cambio en la energía cinética es la suma de los dos. Para el intervalo más largo de A a C (segundo diagrama), la gravedad continúa haciendo trabajo negativo hasta que se ha ido toda la energía cinética de la pelota. Para el intervalo de C a B, la única fuerza externa es la gravedad, que ahora hace un trabajo positivo, igual al incremento en la energía cinética de la pelota.
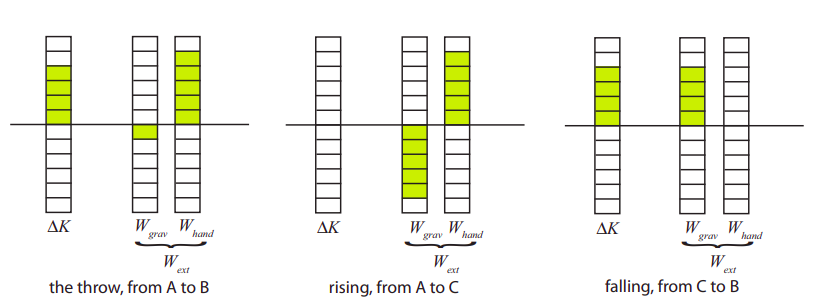
Por supuesto, el valor numérico del trabajo real realizado por alguna fuerza en particular no depende de nuestra elección del sistema: en cada caso, la gravedad hace la misma cantidad de trabajo en los procesos ilustrados en la Figura\(\PageIndex{2}\) que en los ilustrados en la Figura\(\PageIndex{1}\). La diferencia, sin embargo, es que para el sistema de la Figura\(\PageIndex{2}\), la gravedad es una fuerza externa, y ahora el trabajo que realiza realmente cambia la energía total del sistema, porque la energía potencial gravitacional ahora no está incluida en ese total.
Formalmente, funciona así: en el caso que se muestra en la Figura\(\PageIndex{1}\), donde el sistema es la bola y la tierra, tenemos\(\Delta K + \Delta U^G = W_{hand}\). Por el resultado (\ ref {eq:7.18}), sin embargo, tenemos\(\Delta U^G = −W_{grav}\), y así esta ecuación se puede reorganizar para leer\(\Delta K = W_{grav} + W_{hand}\), que es solo el resultado (\ ref {eq:7.20}) cuando el sistema es el balón solo.
En última instancia, la razón por la que enfatizamos la importancia de la elección del sistema es evitar el doble conteo: si quieres contar el trabajo realizado por gravedad como contribuyendo al cambio en la energía total del sistema, significa que estás, implícitamente, tratando la gravedad como una fuerza externa, y por lo tanto tu sistema debe ser algo que no tenga, por sí misma, energía potencial gravitacional (el caso de la bola en la Figura\(\PageIndex{2}\)); a la inversa, si insistes en contar la energía potencial gravitacional como una contribución a la energía total del sistema, entonces debes tratar a la gravedad como una fuerza interna, y dejarla fuera del cálculo del trabajo realizado en el sistema por las fuerzas externas, que son las únicas que pueden cambiar la energía total del sistema.
El caso general: sistemas con disipación
Ahora estamos listos para considerar qué sucede cuando algunas de las interacciones internas en un sistema no son conservadoras. Hay dos observaciones clave a tener en cuenta: primero, por supuesto, que la energía siempre se conservará en un sistema cerrado, independientemente de que las fuerzas internas sean “conservadoras” o no: si no lo son, simplemente significa que convertirán parte de la energía mecánica “organizada”, en desorganizada ( principalmente térmica).
La segunda observación es que el trabajo realizado por una fuerza externa sobre un sistema no depende de dónde proviene la fuerza, es decir, qué disposición física utilizamos para producir la fuerza. Sólo el valor de la fuerza en cada paso y el desplazamiento del punto de aplicación están involucrados en la definición (7.2.6). Esto significa, en particular, que podemos usar una interacción conservadora para hacer el trabajo por nosotros. Resulta, entonces, que la generalización del resultado (\ ref {eq:7.20}) para aplicar a todo tipo de interacciones se vuelve sencilla.
Para ver la idea, considere, por ejemplo, la situación en la Figura\(\PageIndex{3}\) a continuación. Esto es esencialmente lo mismo que la Figura 6.3.1, que analizamos en detalle desde la perspectiva de fuerzas y aceleraciones en el capítulo anterior. Aquí lo he descompuesto en dos sistemas. El sistema A, delineado en azul, consiste en el bloque 1 y la superficie sobre la que se desliza, e incluye una interacción disipativa, es decir, fricción cinética, entre el bloque y la superficie. La fuerza que hace trabajo en este sistema es la fuerza de tensión de la cuerda,\(\vec F^t_{r,1}\).
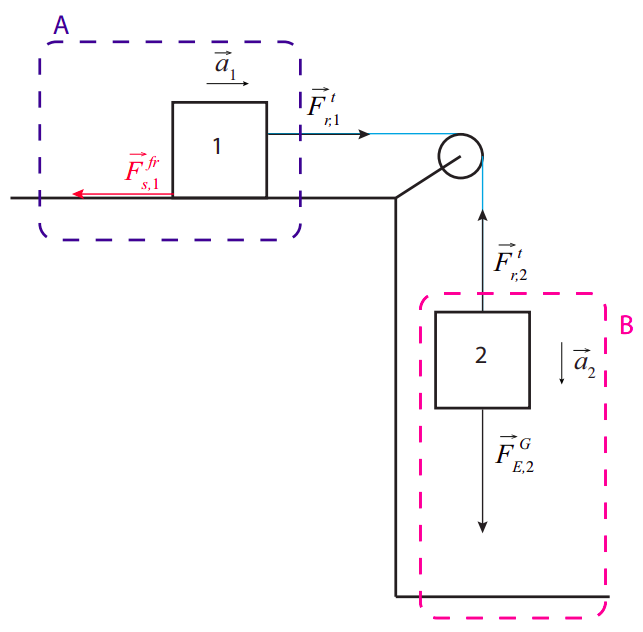
Debido a que se supone que la cuerda tiene una masa insignificante, esta fuerza es la misma en magnitud que la fuerza\(\vec F^t_{r,2}\) que está haciendo trabajo negativo en el sistema B. El sistema B, delineado en magenta, consiste en el bloque 2 y la tierra y por lo tanto incluye solo una interacción interna, a saber, la gravedad, que es conservador. Esto significa que podemos aplicarle inmediatamente el teorema (\ ref {eq:7.20}), y concluir que el trabajo realizado sobre B by\(\vec F^t_{r,2}\) es igual al cambio en la energía total del sistema B:
\[ W_{r, B}=\Delta E_{B} \label{eq:7.23} .\]
Sin embargo, como la cuerda es inextensible, los dos bloques se mueven la misma distancia al mismo tiempo, y la fuerza ejercida sobre cada uno por la cuerda es la misma en magnitud, por lo que el trabajo realizado por la cuerda en el sistema A es igual en magnitud pero opuesto en signo al trabajo que realiza en el sistema B:
\[ W_{r, A}=-W_{r, B}=-\Delta E_{B} \label{eq:7.24} .\]
Consideremos ahora el sistema total formado por A+B. Suponiendo que se trata de un sistema cerrado, su energía total debe ser constante, por lo que cualquier cambio en la energía total de B debe ser igual y opuesto al cambio correspondiente en la energía total de A:\(\Delta E_B = −\Delta E_A\). Por lo tanto,
\[ W_{r, A}=-\Delta E_{B}=\Delta E_{A} \label{eq:7.25} .\]
Por lo que concluimos que el trabajo realizado por la fuerza externa sobre el sistema A debe ser igual al cambio total en la energía del sistema A. En otras palabras, la Ecuación (\ ref {eq:7.20}) se aplica también al sistema A, como lo hace al sistema B, aunque la interacción entre las partes que componen el sistema A sea disipativa.
Aunque he demostrado que esto es cierto solo para un ejemplo específico, el argumento es bastante general: si utilizo un sistema conservador B para hacer algún trabajo en otro sistema A, suceden dos cosas: primero, en virtud de (\ ref {eq:7.20}), el trabajo realizado por B viene a expensas de su energía total, entonces\(W_{ext,A} = −\Delta E_B\). Segundo, si A y B juntos forman un sistema cerrado, el cambio en la energía de A debe ser igual y opuesto al cambio en la energía de B, entonces\(\Delta E_A = −\Delta E_B = W_{ext,A}\). Entonces el resultado (\ ref {eq:7.20}) se mantiene para A, independientemente de si sus interacciones internas son conservadoras o no.
Lo esencial en el razonamiento anterior es que A y B juntos deben formar un sistema cerrado, es decir, uno que no intercambie energía con su entorno. Es muy importante, por lo tanto, si queremos aplicar el teorema (\ ref {eq:7.20}) a un sistema general —es decir, uno que incluya interacciones disipativas— que traquemos el límite del sistema de tal manera que se garantice que no se produzca disipación alguna en el límite. Por ejemplo, en la situación ilustrada en la Figura\(\PageIndex{3}\), si queremos que se aplique el resultado (\ ref {eq:7.25}) debemos tomar el sistema A para incluir tanto el bloque 1 como la superficie sobre la que se desliza. La razón de esto es que la energía “disipada” por la fricción cinética cuando dos objetos se frotan entre sí entra en ambos objetos. Entonces, a medida que el bloque se desliza, la fricción cinética está convirtiendo parte de su energía cinética en energía térmica, pero no toda esta energía térmica permanece dentro del bloque 1. Dicho de otra manera, ante la presencia de fricción, el bloque 1 por sí mismo no es un sistema cerrado: es “fuga” de energía a la superficie. Por otro lado, cuando incluyes (suficiente) la superficie en el sistema, puedes estar seguro de haber “atrapado” toda la energía disipada, y aplica el resultado (\ ref {eq:7.20}).
Energía disipada por fricción cinética
En la situación ilustrada en la Figura\(\PageIndex{3}\), podríamos calcular la energía disipada por fricción cinética por medios indirectos. Por ejemplo, podemos usar el hecho de que la energía del sistema A es de dos clases, cinética y “disipada”, y por lo tanto, por teorema (\ ref {eq:7.20}), tenemos
\[\Delta K+\Delta E_{d i s s}=F_{r, 1}^{t} \Delta x_{1} \label{eq:7.26} .\]
De vuelta en la sección 6.3, utilizamos las leyes de Newton para resolver la aceleración de este sistema y la tensión en la cuerda; usando esos resultados, podemos calcular el desplazamiento\(\Delta x_1\) en cualquier intervalo de tiempo, y el cambio correspondiente en\(K\), y luego podemos resolver la Ecuación (\ ref {eq:7.26}) para\(\Delta E_{diss}\).
Si hacemos esto, nos enteraremos de que, de hecho, se mantiene el siguiente resultado,
\[ \Delta E_{d i s s}=-F_{s, 1}^{k} \Delta x_{1} \label{eq:7.27} \]
donde\(F^k_{s,1}\) está la fuerza de fricción cinética ejercida por la superficie sobre el bloque 1, y debe entenderse como negativa en esta ecuación (para que\(\Delta E_{diss}\) salga positiva, como debe ser).
Es tentador pensar en el producto\(F^k_{s,1}\Delta x\) como el trabajo realizado por la fuerza de la fricción cinética sobre el bloque, y la mayoría de las veces no hay nada malo en eso, pero es importante darse cuenta de que el “punto de aplicación” de la fuerza de fricción no es un solo punto: más bien, la fuerza se “distribuye”, es decir, repartidas por toda el área de contacto entre el bloque y la superficie. Como consecuencia de esto, una expresión más general de la energía disipada por la fricción cinética entre un objeto\(o\) y una superficie\(s\) debería ser
\[ \Delta E_{\text {diss}}=\left|F_{s, o}^{k} \| \Delta x_{s o}\right| \label{eq:7.28} \]
donde estoy usando la notación subíndice del Capítulo 1\(x_{AB}\) para referirme a “la posición de B en el marco de A” (o “relativo a A”); en otras palabras,\(\Delta x_{so}\) es el cambio en la posición del objeto relativo a la superficie o, más simplemente, la distancia que el objeto y la superficie se deslizan más allá entre sí (mientras se frotan unos contra otros, y por lo tanto disipan energía). Si las superficies están en reposo (relativo a la Tierra), se\(\Delta x_{so}\) reduce a\(\Delta x_{Eo}\), el desplazamiento del objeto en el marco de referencia de la Tierra, y podemos eliminar el subíndice\(E\), como solemos hacer, por simplicidad; sin embargo, en los raros casos en que tanto la superficie como el objeto se mueven (como en parte (c) del Ejercicio 6.7.4 en el Capítulo 6, el problema del trineo) lo que importa es hasta qué punto se mueven entre sí. En ese caso tenemos\( \left|\Delta x_{s o}\right|=\left|\Delta x_{o}-\Delta x_{s}\right| \) (con ambos\(\Delta x_o\) y\(\Delta x_s\) medidos en el marco de referencia de la Tierra).


