7.2: Trabajo sobre una sola partícula

Considera una partícula que sufre un desplazamiento\(\Delta x\) mientras una fuerza constante\(F\) actúa sobre ella. En una dimensión, el trabajo realizado por la fuerza sobre la partícula se define por

\[ W = F \Delta x \quad (\mathrm{constant \: force}) \label{eq:7.4} \]

y es positivo si la fuerza y el desplazamiento tienen el mismo signo (es decir, si apuntan en la misma dirección), y negativo de lo contrario.

En tres dimensiones, la fuerza será un vector\(\vec F\) con componentes (\(F_x, F_y, F_z\)), y el desplazamiento, así mismo, será un vector\(\Delta \vec r\) con componentes (\(\Delta x, \Delta y, \Delta z\)). El trabajo se definirá entonces como

\[ W=F_{x} \Delta x+F_{y} \Delta y+F_{z} \Delta z \label{eq:7.5} .\]

Esta expresión es una instancia de lo que se conoce como el producto punto (o producto interno, o producto escalar) de dos vectores. Dados dos vectores\(\vec A\) y\(\vec B\), su producto puntual se define, en términos de sus componentes,

\[ \vec{A} \cdot \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \label{eq:7.6} .\]

Esto también se puede expresar en términos de las magnitudes de los vectores, |\(\vec A\) | y |\(\vec B\) |, y el ángulo que forman, en la siguiente forma:

\[ \vec{A} \cdot \vec{B}=|\vec{A}||\vec{B}| \cos \phi \label{eq:7.7} \]

Figura\(\PageIndex{1}\): Ilustrando el ángulo\(\phi\) a utilizar al calcular el producto de punto de dos vectores mediante la fórmula (\ ref {eq:7.7}). Una forma de pensar en esta fórmula es tomar la proyección de vector\(\vec A\) sobre vector\(\vec B\) (indicado aquí por las líneas azules), que es igual a\( |\vec{A}| \cos \phi \), luego multiplicar eso por la longitud de\(\vec B\) (o viceversa, por supuesto).

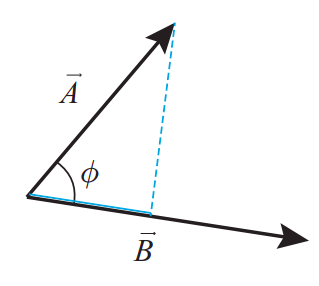
La figura\(\PageIndex{1}\) muestra lo que quiero decir con el ángulo\(\phi\) en esta expresión. La igualdad de las dos definiciones, Eqs. (\ ref {eq:7.6}) y (\ ref {eq:7.7}), se demuestra en los libros de texto de matemáticas. La ventaja de la Ecuación (\ ref {eq:7.7}) es que es independiente de la elección de un sistema de coordenadas.

Usando la notación de producto punto, el trabajo realizado por una fuerza constante se puede escribir como

\[ W=\vec{F} \cdot \Delta \vec{r} \label{eq:7.8} .\]

La ecuación (\ ref {eq:7.7}) muestra entonces que, como mencioné en la introducción, cuando la fuerza es perpendicular al desplazamiento (\(\phi = 90^{\circ}\)) el trabajo que realiza es cero. También puedes ver esto directamente desde la Ecuación (\ ref {eq:7.5}), eligiendo el\(x\) eje para apuntar en la dirección de la fuerza (so\(F_y\) =\(F_z\) = 0), y el desplazamiento para apuntar a lo largo de cualquiera de los otros dos ejes (so\(\Delta x\) = 0): el resultado es\(W\) = 0.

Si la fuerza no es constante, nuevamente seguimos el procedimiento estándar de descomponer el desplazamiento total en pedazos que son lo suficientemente cortos para que la fuerza pueda tomarse como constante sobre cada uno de ellos, calculando todas esas “piezas de trabajo” (posiblemente muy pequeñas), y sumarlas todas juntas. En una dimensión, el resultado final puede expresarse como la integral

\[ W=\int_{x_{i}}^{x_{f}} F(x) d x \quad(\text { variable force }) \label{eq:7.9} .\]

Entonces el trabajo viene dado por el “área” bajo la\(x\) curva\(F\) -vs-. En más dimensiones, tenemos que escribir una especie de integral multivariable conocida como integral de línea. Eso es cálculo avanzado, así que no vamos a ir ahí este semestre.

Trabajo realizado por la fuerza neta y el teorema de trabajo-energía

Tanto para las matemáticas y las definiciones. ¿Dónde entra la energía? Supongamos que esa\(F\) es la única fuerza o la fuerza neta sobre la partícula, la suma de todas las fuerzas que actúan sobre la partícula. Nuevamente, por simplicidad asumiremos que es constante (no cambia) mientras la partícula sufre el desplazamiento\(\Delta x\). Sin embargo, ahora\(\Delta x\) y\(F_{net}\) están relacionados: una fuerza neta constante significa una aceleración constante,\(a = F_{net}/m\), y para la aceleración constante sabemos que\(v^2_f − v^2_i = 2a \Delta x\) se aplica la fórmula. Por lo tanto, podemos escribir

\[ W_{n e t}=F_{n e t} \Delta x=m a \Delta x=m \frac{1}{2}\left(v_{f}^{2}-v_{i}^{2}\right) \label{eq:7.10} \]

que es decir

\[ W_{n e t}=\Delta K \label{eq:7.11} .\]

En palabras, el trabajo realizado por la fuerza neta que actúa sobre una partícula a medida que se mueve equivale al cambio en la energía cinética de la partícula en el transcurso de su desplazamiento. Este resultado a menudo se conoce como el Teorema del Trabajo y la Energía.

Como habrás adivinado por nuestro llamarlo un “teorema”, el resultado (\ ref {eq:7.11}) es muy general. Se sostiene en tres dimensiones, y se mantiene también cuando la fuerza no es constante durante todo el desplazamiento, solo hay que usar la ecuación correcta para calcular el trabajo en esos casos. Se aplicaría al trabajo realizado por la fuerza neta sobre un objeto extendido, también, siempre que esté bien tratar el objeto extendido como una partícula, así que básicamente, un objeto rígido que se mueve como un todo y no hace nada elegante como girar mientras lo hace.

Otra dirección posible en la que generalizar (\ ref {eq:7.11}) podría ser la siguiente. Por definición, una “partícula” no tiene otro tipo de energía, además de la energía cinética (traslacional). También, y por la misma razón (es decir, la ausencia de estructura interna), no tiene fuerzas “internas” —todas las fuerzas que actúan sobre ella son externas. Así —para este sistema tan simple— podríamos reformular el resultado (\ ref {eq:7.11}) diciendo que el trabajo realizado por la fuerza externa neta que actúa sobre el sistema (la partícula en este caso) es igual al cambio en su energía total. De hecho es en esta forma que finalmente generalizaremos (\ ref {eq:7.11}) para tratar con sistemas arbitrarios.

Antes de ir allí, sin embargo, me gustaría tomar un pequeño desvío para explorar otra extensión “razonable” del resultado (\ ref {eq:7.11}), así como sus limitaciones.