8.1: Tratar con las fuerzas en dos dimensiones

Hemos podido obtener mucha física de nuestro estudio del movimiento (en su mayoría) solo unidimensional, pero no hace falta decir que el mundo real es mucho más rico que eso, y hay una serie de fenómenos nuevos e interesantes que aparecen cuando se considera el movimiento en dos o tres dimensiones. El propósito de este capítulo es presentarte algunas de las situaciones bidimensionales más simples de interés físico.

Una característica común a todos estos problemas es que las fuerzas que actúan sobre los objetos bajo consideración normalmente no se alinearán con los desplazamientos. Esto significa, en la práctica, que debemos prestar más atención a la naturaleza vectorial de estas cantidades de lo que hemos hecho hasta ahora. Esta sección presentará un breve recordatorio de algunas propiedades básicas de los vectores, e introducirá un par de principios simples para el análisis de los sistemas que seguirán.

Para empezar, recordemos que un vector es una cantidad que tiene tanto una magnitud como una dirección. La magnitud del vector solo nos dice lo grande que es: la magnitud del vector de velocidad, por ejemplo, es la velocidad, es decir, qué tan rápido se mueve algo. Al trabajar con vectores en una dimensión, normalmente hemos asumido que todo el vector (ya sea una velocidad, una aceleración o una fuerza) yacía a lo largo de la línea de movimiento del sistema, y todo lo que tuvimos que hacer para indicar la dirección era darle a la magnitud del vector un signo apropiado. Para los problemas que siguen, sin embargo, se volverá fundamental descomponer los vectores en sus componentes a lo largo de un conjunto apropiado de ejes. Esto implica geometría muy simple, y sigue el ejemplo del vector de posición\(\vec r\), cuyos componentes son solo las coordenadas cartesianas del punto que localiza en el espacio (como se muestra en la Figura 1.2.1). Para un vector genérico, por ejemplo, una fuerza, como la que se muestra en la Figura\(\PageIndex{1}\) a continuación, los componentes\(F_x\) y se\(F_y\) pueden obtener de un triángulo rectángulo, como ahí se indica:

Figura\(\PageIndex{1}\):: Los componentes de un vector que forma un ángulo\(\theta\) con el\(x\) eje positivo. Se muestran dos ejemplos, para\(\theta < 90^{\circ}\) (en cuyo caso\(F_x \) > 0) y para\(90^{\circ} < \theta < 180^{\circ}\) (en cuyo caso\(F_x\) < 0). En ambos casos,\(F_y\) > 0.

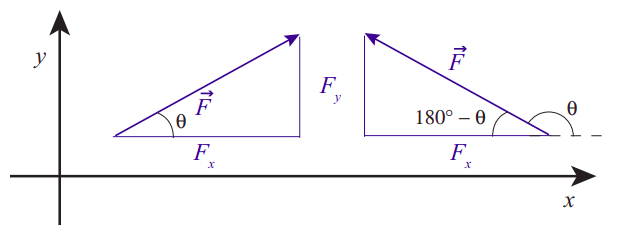
El triángulo siempre tendrá la magnitud del vector (\(|\vec{F}|\)en este caso) como hipotenuso. Los otros dos lados deben ser paralelos a los ejes de coordenadas. Sus longitudes son los componentes correspondientes, a excepción de un signo que depende de la orientación del vector. Si por casualidad conocemos el ángulo\(\theta\) que hace el vector con el\(x\) eje positivo, siempre se mantendrán las siguientes relaciones:

\ begin {align}
F_ {x} &=|\ vec {F} |\ cos\ theta\ nonumber\\
F_ {y} &=|\ vec {F} |\ sin\ theta\ nonumber\\
|\ vec {F} | &=\ sqrt {F_ {x} ^ {2} +F_ {y} ^ {2}}\ nonumber er\\
\ theta &=\ tan ^ {-1}\ frac {F_ {y}} {F_ {x}}\ label {eq:8.1}.
\ end {align}

Obsérvese, sin embargo, que en general este ángulo\(\theta\) puede no ser uno de los ángulos interiores del triángulo (como se muestra en el diagrama derecho en la Figura\(\PageIndex{1}\)), y que en ese caso puede ser más sencillo calcular la magnitud de los componentes usando trigonometría y un ángulo interior (como 180 \(^{\circ} − \theta\)en el ejemplo), y darles los letreros apropiados “a mano”. En el ejemplo de la derecha, la longitud del lado horizontal del triángulo es igual a\( |\vec{F}| \cos \left(180^{\circ}-\theta\right) \), que es una cantidad positiva; el valor correcto para\(F_x\), sin embargo, es el número negativo\(|\vec{F}| \cos \theta=-|\vec{F}| \cos \left(180^{\circ}-\theta\right)\).

En todo caso, es importante no obsesionarse con la noción de que “el\(x\) componente siempre será proporcional al coseno de”\(\theta\). El símbolo\(\theta\) es solo uno conveniente para usar para un ángulo genérico. Hay cuatro secciones en este capítulo, y en cada una hay un\(\theta\) usado con un significado diferente. En caso de duda, simplemente dibuja el triángulo rectángulo apropiado y recuerda de tus clases de trigonometría qué lado va con el seno, y cuál con el coseno.

Para los problemas que vamos a estudiar en este capítulo, la idea es romper todas las fuerzas involucradas en componentes a lo largo de ejes de coordenadas adecuadamente elegidos, luego agregar todos los componentes a lo largo de cualquier dirección dada, y aplicar a\(F_{net} = ma\) lo largo de esa dirección: es decir, escribiremos (y eventualmente resolveremos ) las ecuaciones

\ begin {align}
&F_ {n e t, x} =m a_ {x}\ nonumber\\
&F_ {n e t, y} =m a_ {y}\ label {eq:8.2}.
\ end {align}

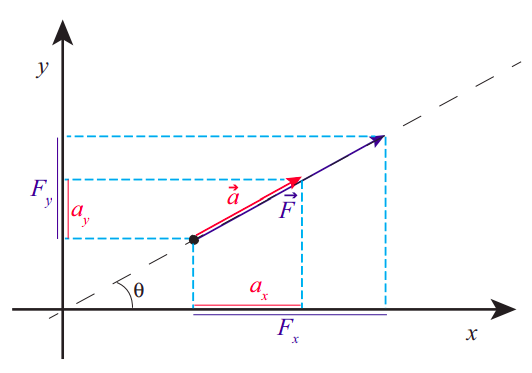
Podemos demostrar que Eqs. (\ ref {eq:8.2}) debe sostenerse para cualquier elección de ortogonal\(x\) y\(y\) ejes, basado en el hecho de que sabemos que se\(\vec F_{net} = m\vec a\) sostiene a lo largo de una dirección particular, es decir, la dirección común a\(\vec F_{net}\) y\(\vec a\), y el hecho de que hemos definido el procedimiento de proyección para que sea el mismo para cualquier tipo de vector. La figura\(\PageIndex{2}\) muestra cómo funciona esto. A lo largo de la línea discontinua solo se tiene la situación que por ahora nos resulta familiar a partir de problemas unidimensionales, donde\(\vec a\) yace a lo largo\(\vec F\) (se supone que aquí es la fuerza neta), y\( |\vec{F}|=m|\vec{a}|\). No obstante, en la figura he elegido los ejes para hacer un ángulo\(\theta\) con esta dirección. Entonces, si miras las proyecciones de\(\vec F\) y\(\vec a\) a lo largo del\(x\) eje, encontrarás

\ begin {align}
a_ {x} &=|\ vec {a} |\ cos\ theta\ nonumber\\
F_ {x} &=|\ vec {F} |\ cos\ theta=m|\ vec {a} |\ cos\ theta=m a_ {x}\ label {eq:8.3}
\ end align {}

y de manera similar,\(F_y = ma_y\). En palabras, cada componente del vector de fuerza es responsable únicamente del componente correspondiente de la aceleración. Una fuerza en la\(x\) dirección no causa ninguna aceleración en la\(y\) dirección, y viceversa.

Figura\(\PageIndex{2}\): Si tomas la forma familiar, unidimensional (ver la línea discontinua negra) de\(\vec F = m\vec a\), y la proyectas sobre ejes ortogonales girados, obtienes el caso bidimensional general, mostrando que cada componente ortogonal de la aceleración es proporcional, a través de la masa\(m\), a solo el componente correspondiente de la fuerza (Eqs. (\ ref {eq:8.2})).

En el resto del capítulo veremos cómo usar las Eqs. (\ ref {eq:8.2}) en varios ejemplos. Una cosa que puedo anticipar es que, en general, intentaremos elegir nuestros ejes (a diferencia de la Figura\(\PageIndex{2}\) anterior) para que uno de ellos sí coincida con la dirección de la aceleración, por lo que el movimiento a lo largo de la otra dirección es inexistente (\(v\)= 0) o trivial (velocidad constante).