8.2: Movimiento de proyectiles
- Page ID
- 128346
El movimiento del proyectil es básicamente solo caída libre, solo con el entendimiento de que el objeto que estamos rastreando fue “proyectado” o “disparado”, con cierta velocidad inicial (en lugar de simplemente caer del reposo). A diferencia de los casos anteriores de caída libre que hemos estudiado hasta ahora, ahora asumiremos que la velocidad inicial tiene una componente horizontal, como resultado de lo cual, en lugar de simplemente ir hacia arriba y/o hacia abajo, el objeto describirá (ignorando la resistencia al aire, como de costumbre) una parábola en una vertical avión.
El plano en cuestión está determinado por la velocidad inicial (más precisamente, la componente horizontal de la velocidad inicial) y la gravedad. En la Figura se muestra una trayectoria genérica\(\PageIndex{1}\), mostrando los vectores de fuerza y aceleración (constante a lo largo) y el vector de velocidad en varios puntos a lo largo de la trayectoria.
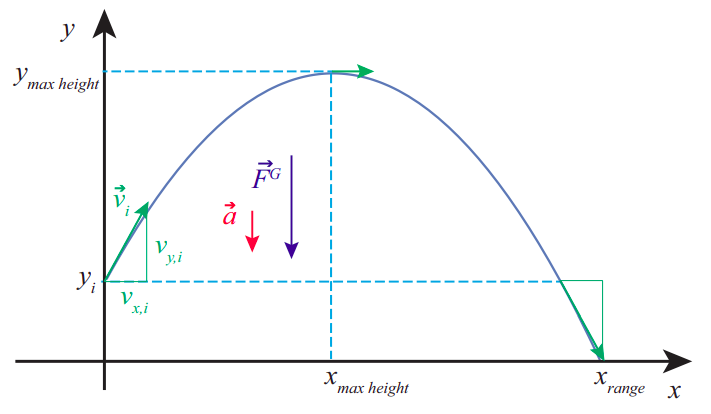
Conceptualmente, el problema resulta sumamente sencillo si aplicamos el principio básico introducido en la Sección 8.1. La fuerza es vertical en todo momento; así, después del lanzamiento, no hay aceleración horizontal, y la aceleración vertical es justa\(−g\), tal como siempre lo fue en nuestros anteriores problemas onedimensionales de caída libre:
El movimiento general, entonces, es una combinación de movimiento con velocidad constante horizontalmente, y movimiento con aceleración constante verticalmente, y podemos anotar las ecuaciones correspondientes de movimiento inmediatamente:
donde (\(x_i, y_i\)) son las coordenadas del punto de lanzamiento (generalmente no hay razón para hacer otra\(x_i\) cosa que no sea cero, así que lo haremos a continuación), y (\(v_{x,i}, v_{y,i}\)) los componentes iniciales del vector de velocidad.
Al eliminar\(t\) entre las dos últimas Eqs. (\ ref {eq:8.5}), obtenemos la ecuación de la trayectoria en el\(y\) plano\(x\) -:
\[ y=y_{i}+\frac{v_{y, i}}{v_{x, i}} x-\frac{g}{2 v_{x, i}^{2}} x^{2} \label{eq:8.6} \]
que, como se indicó anteriormente, y como se muestra en la Figura\(\PageIndex{1}\), es efectivamente la ecuación de una parábola.
El ápice de la parábola (punto más alto de la trayectoria) está en\(x_{max \: height} = v_{x,i}v_{y,i}/g\). Podemos obtener este resultado del cálculo, o de una comparación de la Ecuación (\ ref {eq:8.6}) con la forma canónica de una parábola, o podemos usar alguna física: la altura máxima se alcanza, como de costumbre, cuando la velocidad vertical se vuelve momentáneamente cero, así resolviendo la\(v_y\) ecuación (\ ref {eq:8.5}) para\(t_{max \: height}\) y sustituyendo en la\(x\) ecuación, obtenemos
La última de estas ecuaciones debería parecer familiar. Es, de hecho, una variación de nuestro viejo amigo\(v^2_f − v^2_i = −2g\Delta y\), solo que ahora en lugar de la velocidad completa\(\vec v\) tenemos que usar solo el componente de velocidad vertical\(v_y\). Al igual que para el movimiento unidimensional, este resultado se deriva nuevamente de la conservación de la energía: a lo largo del vuelo, debemos tener\(K + U^G\) = constante, solo que ahora hay un componente de la energía cinética —la parte asociada al movimiento horizontal— que permanece constante por sí sola. En general, la energía cinética de una partícula será\(\frac{1}{2}m|\vec v|^2\), donde\(|\vec v|\) está la magnitud del vector de velocidad, es decir, la velocidad. En dos dimensiones, esto da
\[ K=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2} \label{eq:8.8} .\]
Para el movimiento de proyectiles, sin embargo,\(v_x\) no cambia, por lo que cualquier cambio en\(K\) afectará solo al segundo término en la Ecuación (\ ref {eq:8.8}). Conservación de energía entre dos instantes\(i\) y\(f\) da
\[ K+U^{G}=\frac{1}{2} m v_{x, i}^{2}+\frac{1}{2} m v_{y, i}^{2}+m g y_{i}=\frac{1}{2} m v_{x, i}^{2}+\frac{1}{2} m v_{y, f}^{2}+m g y_{f} \label{eq:8.9} .\]
El\(\frac{1}{2}mv^2_{x,i}\) término cancela, y por lo tanto
\[ v_{y, f}^{2}-v_{y, i}^{2}=-2 g\left(y_{f}-y_{i}\right) \label{eq:8.10} .\]
Otra cantidad de interés es el alcance del proyectil, o la distancia horizontal máxima recorrida. Podemos calcularlo a partir de Eqs. (\ ref {eq:8.5}), estableciendo\(y\) igual a la altura final, luego resolviendo for\(t\) (que generalmente requiere resolver una ecuación cuadrática), y luego sustituir el resultado en la ecuación por\(x\). En el caso sencillo cuando la altura final sea la misma que la altura inicial, podemos evitar la necesidad de calcular en conjunto, y razón justa, por el hecho de que la trayectoria es simétrica, que la distancia horizontal total recorrida será el doble de la distancia hasta el punto donde se alcanza la altura máxima, es decir,\(x_{range} = 2x_{max \: height}\):
\[ x_{\text {range }} = \frac{2 v_{x, i} v_{y, i}}{g} \quad \text { (only if }\left.y_{f}=y_{i}\right) \label{eq:8.11} .\]
Como puede ver, todas estas ecuaciones dependen de los valores iniciales de los componentes del vector de velocidad\(\vec v_i\). Si\(\vec v_i\) hace un ángulo\(\theta\) con la horizontal, y simplificamos la notación llamando a su magnitud\(v_i\), entonces podemos escribir
\ begin {align}
&v_ {x, i} =v_ {i}\ cos\ theta\ nonumber\\
&v_ {y, i} =v_ {i}\ sin\ theta\ label {eq:8.12}
\ end {align}
En términos de\(v_i\) y\(\theta\), la ecuación de rango (\ ref {eq:8.11}) se convierte en
\[ x_{\text {range }}=\frac{v_{i}^{2} \sin (2 \theta)}{g} \quad \text { (only if } y_{f}=y_{i}) \label{eq:8.13} \]
ya que\(2 \sin \theta \cos \theta = \sin(2\theta)\). Esto nos dice que para cualquier velocidad de lanzamiento dada, el rango máximo se logra cuando el ángulo de lanzamiento\(\theta = 45^{\circ}\) (siempre asumiendo que la altura final es la misma que la altura inicial).
En la vida real, por supuesto, siempre habrá resistencia al aire, y todos estos resultados se modificarán un poco. Matemáticamente, las cosas se vuelven mucho más complicadas: la fuerza de arrastre depende de la velocidad, que involucra ambos componentes de la velocidad, por lo que los movimientos horizontal y vertical ya no están desacoplados: no solo hay ahora un\(F_x\), sino que su valor en un momento dado depende tanto de\(v_x\) y\(v_y\). Físicamente, se puede pensar en la fuerza de arrastre como hacer un trabajo negativo en el proyectil y, por lo tanto, eliminar la energía cinética del mismo. Menos energía cinética significa, básicamente, que no viajará tan lejos ni vertical ni horizontalmente. Sorprendentemente, el ángulo óptimo de lanzamiento permanece bastante cerca de 45\(^{\circ}\), al menos si las simulaciones en este enlace son precisas:


