12.1: Olas Viajeras
- Page ID
- 128456
En nuestro estudio de la mecánica hemos tratado hasta ahora con objetos parecidos a partículas (objetos que solo tienen energía traslacional), y objetos extendidos y rígidos, que también pueden tener energía rotacional. Sin embargo, hemos asumido implícitamente que todos los objetos que estudiamos tenían alguna estructura interna, o eran en cierta medida deformables, siempre que permitíamos la posibilidad de que almacenaran otras formas de energía, como la química o la térmica.
Este capítulo trata de un tipo muy común de movimiento organizado (en contraposición al incoherente) exhibido por objetos elásticos extendidos, a saber, el movimiento de las olas. (A menudo, el “objeto” en el que tiene lugar el movimiento de las olas se llama “medio”). Las olas pueden ser “viajando” o “de pie”, y comenzaremos por el tipo viajero, ya que son las que más claramente exhiben las características típicamente asociadas con el movimiento de las olas.
Una onda viajera en un medio es una perturbación del medio que se propaga a través de ella, en una dirección definida y con una velocidad definida. Por una “perturbación” normalmente nos referimos a un desplazamiento de las partes que componen el medio, alejándose de su posición de reposo o equilibrio. La idea aquí es considerar cada parte de un medio elástico como, potencialmente, un oscilador, que se acople a las partes vecinas empujándolas o tirando de ellas (para un ejemplo de cómo modelar esto matemáticamente, vea el Tema Avanzado 12.6 al final de este capítulo). Cuando la ola viajera alcanza una ubicación particular en el medio, pone en movimiento esa parte del medio, dándole algo de energía e impulso, que luego pasa a una parte vecina, y así sucesivamente en la línea.
Se puede ver un ejemplo de cómo funciona esto en un slinky. Comienza por estirar un poco el slinky, luego agarra algunas bobinas, amontonarlas en un extremo y soltarlas. Deberías ver un “pulso de compresión” viajando por el furgón, con muy poca distorsión; es posible que incluso puedas verlo reflejado en el otro extremo, y regresando, antes de que toda su energía se disipe.
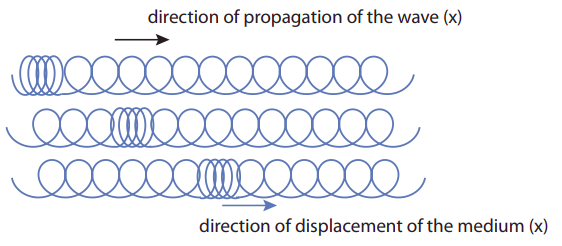
El pulso de compresión en el slinky en la Figura\(\PageIndex{1}\) es un ejemplo de lo que se llama una onda longitudinal, debido a que el desplazamiento de las partes que componen el medio (los anillos, en este caso) tiene lugar a lo largo de la misma dimensión espacial a lo largo de la cual viaja la onda (la dirección horizontal, en la figura). Los ejemplos más importantes de ondas longitudinales son las ondas sonoras, que funcionan un poco como las ondas longitudinales en el furgón: una región de aire (o algún otro medio) se comprime, y a medida que se expande empuja sobre una región vecina, haciendo que se comprima, y pasando la perturbación a lo largo. En el proceso, típicamente se producen regiones de rarefacción (donde la densidad cae por debajo de su valor promedio), junto con las regiones de compresión (densidad aumentada).
Lo opuesto a una onda longitudinal es una onda transversal, en la que el desplazamiento de las partes del medio tiene lugar en una dirección perpendicular a la dirección de desplazamiento de la ola. En realidad también es relativamente fácil producir una onda transversal sobre un slinky: nuevamente, simplemente estírela un poco y dale a un extremo una sacudida vigorosa hacia arriba y hacia abajo. Es, sin embargo, un poco difícil dibujar el pulso resultante en un resorte largo con todas las bobinas, así que en la Figura\(\PageIndex{2}\) a continuación en cambio he dibujado un pulso de onda transversal en una cuerda, que se puede producir de la misma manera. (Las cuerdas tienen otras ventajas: también son más fáciles de describir matemáticamente, y son muy relevantes, particularmente para la producción de sonidos musicales).
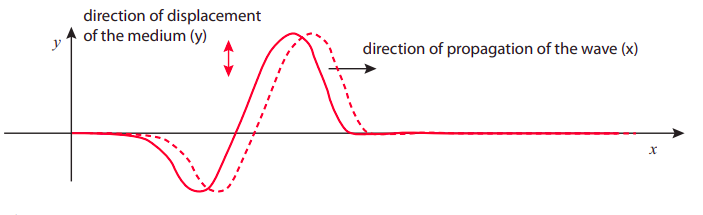
Quizás la propiedad más importante (y notable) del movimiento de las olas es que puede transportar energía e impulso a distancias relativamente largas sin un transporte equivalente de materia. De nuevo, piensa en el furtivo: el “pulso” puede viajar a través de toda la longitud del slinky, llevando consigo impulso y energía, pero cada anillo individual no se aleja mucho de su posición de equilibrio. Idealmente, después de que el pulso haya pasado por una ubicación particular en el medio, la parte correspondiente del medio regresa a su posición de equilibrio y ya no se mueve: toda la energía e impulso que adquirió momentáneamente se pasa hacia adelante. Lo mismo es (idealmente) cierto para la onda transversal en la cuerda en la Figura\(\PageIndex{2}\).
Dado que esto pretende ser una introducción muy elemental a las ondas, consideraré sólo este caso de propagación de onda “ideal” (técnicamente conocida como “lineal y libre de dispersión”), en la que la velocidad de la onda no depende de la forma o tamaño de la perturbación. En ese caso, la perturbación conserva su “forma” a medida que viaja, como he tratado de ilustrar en figuras\(\PageIndex{1}\) y\(\PageIndex{2}\).
La función “Forma de Onda” - Desplazamiento y Velocidad del Medio
En un slinky, lo que he venido llamando las “partes” del medio se ven muy claramente (son, naturalmente, los anillos individuales); en un medio “homogéneo” (uno sin partes visibles), la manera de describir la ola es romper el medio, en tu mente, en infinitamente muchas partes pequeñas o “partículas” (como nosotros han estado haciendo para sistemas extendidos todo el semestre), y anotar ecuaciones que nos digan cómo se mueve cada parte. Físicamente, se debe pensar que cada una de estas “partículas” es lo suficientemente grande como para contener muchas moléculas, pero lo suficientemente pequeñas como para que su posición en el medio pueda estar representada por un punto matemático.
La forma estándar de etiquetar cada “partícula” del medio es por el vector de posición de su posición de equilibrio (el lugar donde la partícula se asienta en reposo en ausencia de una onda). Ante la presencia de la onda, la partícula que inicialmente estaba en reposo en el punto\(\vec{r}\) sufrirá un desplazamiento que voy a representar por el vector\(\vec{\xi}\) (donde\(\xi\) está la letra griega “xi”). Este desplazamiento será en general una función del tiempo, y también puede ser diferente para diferentes partículas, por lo que también será una función de\(\vec{r}\), la posición de equilibrio de la partícula que estamos considerando. La posición de la partícula bajo la influencia de la onda se convierte entonces
\[ \vec{r}+\vec{\xi}(\vec{r}, t) \label{eq:12.1} .\]
Esto es muy general, y se le puede dar una forma más simple para casos simples. Por ejemplo, para una onda transversal en una cuerda, podemos etiquetar cada parte de la cadena en reposo por su\(x\) coordenada, y luego tomar el desplazamiento para que quede a lo largo del\(y\) eje; el vector de posición, entonces, podría escribirse en forma de componente como\( (x, \xi(x, t), 0) \). De igual manera, podemos considerar una onda sonora “plana” como una onda longitudinal que viaja en la\(x\) dirección, donde la densidad del medio es independiente de\(y\) y\(z\) (es decir, es constante en planos perpendiculares a la dirección de propagación). En ese caso, la coordenada de equilibrio\(x\) puede ser utilizada para referirse a una “rebanada” completa del medio, y la posición de esa rebanada, a lo largo del\(x\) eje, en ese momento\(t\) será dada por\(x+\xi(x, t)\). En ambos casos, el vector de desplazamiento se\(\xi\) reduce a un solo componente distinto de cero (a lo largo del\(x\) eje\(y\) o, respectivamente), que puede, por supuesto, ser positivo o negativo. Me limitaré implícitamente a estos casos simples y trataré\(\xi\) como un escalar a partir de este momento.
Bajo estas condiciones, la función\(\xi(x, t)\) (que a menudo se denomina función de onda) nos da la forma de la “onda de desplazamiento”, es decir, el desplazamiento de cada parte del medio, etiquetada por su\(x\) coordenada de equilibrio, en cualquier instante en el tiempo. En consecuencia, tomar la derivada de nos\(\xi\) da la velocidad de la parte correspondiente del medio:
\[ v_{\operatorname{med}}=\frac{d \xi}{d t} \label{eq:12.2} .\]
Esto también es, en general, un vector (a lo largo de la dirección de movimiento de la onda, si la onda es longitudinal, o perpendicular a ella si la onda es transversal). También es una función del tiempo, y en general será diferente de la velocidad de la ola misma, que hemos tomado para ser constante, y que denotaré por el\(c\) contrario.
Ondas armónicas
Una clase importante de ondas son aquellas para las que la función de onda es sinusoidal. Esto significa que las diferentes partes del medio ejecutan movimiento armónico simple, todas con la misma frecuencia, pero cada una (en general) con una fase diferente. Específicamente, para una onda sinusoidal tenemos
\[ \xi(x, t)=\xi_{0} \sin \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right] \label{eq:12.3} .\]
En Ecuación (\ ref {eq:12.3}),\(f\) representa la frecuencia, y juega el mismo papel que hizo en el capítulo anterior: nos dice con qué frecuencia (es decir, cuántas veces por segundo) la parte correspondiente del medio oscila alrededor de su posición de equilibrio. La constante\(\xi_0\) es solo la amplitud de la oscilación (lo que solíamos llamar\(A\) en el capítulo anterior). La constante\(\lambda\), por otro lado, a veces se le conoce como el “período espacial”, o, más a menudo, la longitud de onda de la onda: te dice hasta dónde tienes que viajar a lo largo del\(x\) eje, desde un punto dado\(x\), para encontrar otra que esté realizando la misma oscilación con la misma amplitud y fase.
Un par de instantáneas de una onda armónica se muestran en la Figura\(\PageIndex{3}\). La figura muestra el desplazamiento\(\xi\), en dos momentos diferentes, y en función de la coordenada\(x\) utilizada para etiquetar las partes en las que hemos descompuesto el medio (como se explicó en la subsección anterior). Como tal, la onda que representa podría ser igualmente longitudinal o transversal. Si es transversal, como una onda en una cuerda, entonces puedes pensar que es esencialmente justa\(y\), y luego la curva de\(\xi\) desplazamiento (la línea azul) solo te da la forma de la cuerda. Si la onda es longitudinal, sin embargo, entonces es un poco más difícil visualizar lo que está pasando solo desde la trama de\(\xi (x, t)\). Esto es lo que he intentado hacer con las parcelas de densidad en la parte inferior de la figura.
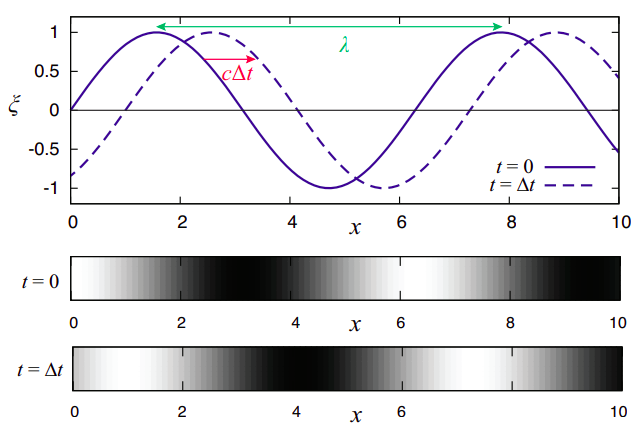
Imagina que la onda es longitudinal, y considera el\(x = \pi\) punto en la curva\(t\) = 0 (el primer cero, sin contar el origen). Una partícula del medio inmediatamente a la izquierda de ese punto tiene un desplazamiento positivo, es decir, se empuja hacia\(x = \pi\), mientras que una rebanada de la derecha tiene un desplazamiento negativo, lo que significa que también es empujada hacia\(x = \pi\). Por lo tanto, esperamos que la densidad del medio sea más alta alrededor de ese punto, mientras que alrededor\(x = 2\pi\) de lo contrario ocurre: las partículas a la izquierda son empujadas hacia la izquierda y las de la derecha son empujadas hacia la derecha, resultando en una región de baja densidad. La gráfica de densidad etiquetada\(t\) = 0 intenta mostrar esto usando una escala de grises donde más oscuro y más claro corresponden a regiones de mayor y menor densidad, respectivamente. Posteriormente las regiones de\(t = \Delta t\) alta y baja densidad se han desplazado una distancia\(c\Delta t\) hacia la derecha, como se muestra en la gráfica de segunda densidad.
Independientemente de si la onda es longitudinal o transversal, si es armónica, el patrón espacial se repetirá cada longitud de onda; se puede pensar en la longitud de onda\(\lambda\) como la distancia entre dos crestas consecutivas (o dos depresiones consecutivas) de la función de desplazamiento, como se muestra en la figura. Si la ola viaja con una velocidad\(c\), un observador sentado en un punto fijo\(x\) vería pasar la perturbación a través de ese punto, las partículas se mueven hacia arriba y hacia abajo (o de un lado a otro), y el movimiento se repite después de que la ola haya recorrido una distancia\(\lambda\), es decir, después de un tiempo \(\lambda/c\). Esto significa que el periodo de la oscilación en cada punto es\(T = \lambda/c\), y la frecuencia correspondiente\(f = 1/T = c/ \lambda\):
\[ f=\frac{c}{\lambda} \label{eq:12.4} .\]
Esta es la ecuación más básica para las ondas armónicas. Haciendo uso de ella, la ecuación (\ ref {eq:12.3}) se puede reescribir como
\[ \xi(x, t)=\xi_{0} \sin \left[\frac{2 \pi}{\lambda}(x-c t)\right] \label{eq:12.5} .\]
Esto sugiere que si queremos que una ola se mueva hacia la izquierda en su lugar, lo único que tenemos que hacer es cambiar el signo del término proporcional a\(c\), lo que efectivamente es el caso.
A diferencia de la velocidad de ola, que es una constante, la velocidad de cualquier parte del medio, con posición de equilibrio\(x\), en ese momento\(t\), puede calcularse a partir de Eqs. (\ ref {eq:12.2}) y (\ ref {eq:12.3})
\[ v_{m e d}(x, t)=2 \pi f \xi_{0} \cos \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right]=\omega \xi_{0} \cos \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right] \label{eq:12.6} \]
(donde he introducido la frecuencia angular\(\omega = 2\pi f\)). Nuevamente, este es un resultado familiar de la teoría del movimiento armónico simple: la velocidad es “90 grados fuera de fase” con el desplazamiento, por lo que es máxima o mínima donde el desplazamiento es cero (es decir, cuando la partícula está pasando por su posición de equilibrio en una dirección u otra).
Obsérvese que el resultado (\ ref {eq:12.6}) implica que, para una onda longitudinal, la “onda de velocidad” está en fase con la “onda de densidad”: es decir, la velocidad media es grande y positiva donde la densidad es mayor, y grande y negativa donde la densidad es menor (compare las gráficas de densidad en Figura\(\PageIndex{3}\)). Si pensamos que el impulso de un elemento de volumen en el medio es proporcional al producto de la densidad y velocidad instantáneas, vemos que para esta onda, que está viajando en la\(x\) dirección positiva, hay más “impulso positivo” que “impulso negativo” en el medio en cualquier momento dado tiempo (claro, si la ola hubiera estado viajando en sentido contrario, el signo de\(v_{med}\) en Ecuación (\ ref {eq:12.6}) habría sido negativo, y habríamos encontrado el resultado opuesto). Esto confirma nuestra expectativa de que la ola lleve una cantidad neta de impulso en la dirección de propagación. Un cálculo detallado (que está más allá del alcance de este libro) muestra que el promedio de tiempo de la “densidad de impulso” (impulso por unidad de volumen) puede escribirse como
\[ \frac{p}{V}=\frac{1}{2 c} \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.7} \]
donde\(\rho_{0}\) es la densidad de masa promedio del medio (masa por unidad de volumen). Curiosamente, ¡este resultado se aplica también a una onda transversal!
Como se mencionó en la introducción, la ola también transporta energía. La ecuación (\ ref {eq:12.6}) podría usarse para calcular la energía cinética de una pequeña región del medio (con volumen\(V\) y densidad\(\rho_{0}\), y por lo tanto\(m=\rho_{0} V\)), y su promedio de tiempo. Esto resulta ser igual al promedio de tiempo de la energía potencial elástica de la misma parte del medio (recordemos que tuvimos el mismo resultado para los osciladores armónicos en el capítulo anterior). Al final, la densidad de energía promediada en el tiempo total (energía por unidad de volumen) en la región del medio ocupado por la onda viene dada por
\[ \frac{E}{V}=\frac{1}{2} \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.8} .\]
Comparando (\ ref {eq:12.7}) y (\ ref {eq:12.8}), puedes ver que
\[ \frac{E}{V}=\frac{c p}{V} \label{eq:12.9} .\]
Esta relación entre las densidades de energía y momento (una es solo\(c\) veces la otra) es un resultado extremadamente general que se aplica a todo tipo de ondas, ¡incluidas las ondas electromagnéticas!
La velocidad de las olas
Se puede preguntar, ¿qué determina la velocidad de una ola en un medio material? La respuesta, cualitativamente hablando, es que\(c\) siempre termina siendo algo de la forma
\[ c \sim \sqrt{\frac{\text { stiffness }}{\text { inertia }}} \label{eq:12.10} \]
donde “rigidez” es alguna medida de lo rígido que es el material (lo difícil que es comprimirlo o, en el caso de una onda transversal, cortarlo), mientras que “inercia” significa algún tipo de densidad de masa.
Para una onda transversal en una cuerda, por ejemplo, encontramos
\[ c=\sqrt{\frac{F t}{\mu}} \label{eq:12.11} \]
donde\(F^t\) esta la tensión en la cuerda y no\(\mu\) es la “masa reducida” de nada (¡perdón por la confusión!) , sino una forma común de escribir la “masa por unidad de longitud” de la cadena. También podríamos simplemente escribir\(\mu = M/L\), donde\(M\) está la masa total de la cadena y\(L\) su longitud. Obsérvese que la tensión es una medida de la rigidez de la cuerda, por lo que ésta es, en efecto, de la forma general (\ ref {eq:12.10}). Para dos cuerdas bajo la misma tensión, pero con densidades diferentes, la ola viajará más lentamente sobre la más densa.
Para una onda de sonido en un fluido (líquido o gas), la velocidad del sonido generalmente se escribe
\[ c=\sqrt{\frac{B}{\rho_{0}}} \label{eq:12.12} \]
donde\(\rho_0\) está la densidad regular (masa por unidad de volumen), y\(B\) es el llamado módulo volumétrico, que da la resistencia del fluido a un cambio de volumen cuando\(P\) se le aplica una presión:\(B = P/(\Delta V /V )\). Entonces, una vez más, obtenemos algo de la forma (\ ref {eq:12.10}). En este caso, sin embargo, encontramos que para muchos fluidos la densidad y la rigidez están ligadas, por lo que aumentan juntos, lo que significa que no podemos simplemente suponer que la velocidad del sonido será automáticamente menor en un medio más denso. Para los gases, esto sí funciona bien: la velocidad del sonido en un gas más ligero, como el helio, es mayor que en el aire, mientras que en un gas más denso como el hexafluoruro de azufre la velocidad del sonido es menor que en el aire 1. No obstante, si comparas la velocidad del sonido en el agua con la velocidad del sonido en el aire, encuentras que es mucho mayor en el agua, ya que el agua es mucho más difícil de comprimir que el aire: en este caso, el aumento de la rigidez compensa con creces el aumento de densidad.
Lo mismo sucede si pasas de un líquido como el agua a un sólido, donde la velocidad del sonido viene dada por
\[ c=\sqrt{\frac{Y}{\rho_{0}}} \label{eq:12.13} \]
donde\(Y\) es, de nuevo, una medida de la rigidez del material, llamada el módulo Young. Dado que un sólido suele ser aún más difícil de comprimir que un líquido, la velocidad del sonido en sólidos como los metales es mucho mayor que en el agua, a pesar de que también son más densos. Para referencia, la velocidad del sonido en acero sería de aproximadamente\(c\) = 5,000 m/s; en agua, alrededor de 1,500 m/s; y en el aire, “solo” de aproximadamente 340 m/s.
1 Este efecto puede ser utilizado para producir “voces divertidas”, debido a la relación\(f = c/\lambda\) (Ecuación (\ ref {eq:12.4})), la cual será discutida con mayor detalle en la sección sobre ondas estacionarias.
Reflejo y Transmisión de Ondas en un Límite Medio
Supongamos que tienes dos medios elásticos diferentes, unidos de alguna manera en un límite común, y tienes una ola en el primer medio viajando hacia el límite. Ejemplos de medios conectados de esta manera podrían ser dos cuerdas diferentes atadas entre sí, o dos resortes con diferentes constantes de resorte unidos en los extremos; o, para las ondas sonoras, podría ser algo así como agua con aire sobre ella: una onda de compresión en el aire que viaja hacia la superficie del agua empujará sobre la superficie del agua y establecer allí una onda de sonido, y viceversa.
Lo primero que hay que notar es que, si la onda incidente tiene una frecuencia\(f\), provocará que el límite medio, cuando llegue ahí, oscile a esa frecuencia. Como resultado de ello, la onda que se configura en el segundo medio —que llamamos onda transmitida — también tendrá la misma frecuencia\(f\). De nuevo, piense en las dos cuerdas atadas entre sí, así que la primera cuerda “impulsa” la segunda a la frecuencia\(f\); o el sonido en el límite aire-agua, conduciendo (empujando) la superficie del agua a la frecuencia\(f\).
Entonces, las ondas incidentes y transmitidas tendrán la misma frecuencia, pero es claro que, si las velocidades de onda en los dos medios son diferentes, no pueden tener la misma longitud de onda: ya que la relación (\ ref {eq:12.4}) tiene que aguantar, nosotros tendremos\(\lambda_1 = c_1/f\), y\(\lambda_2 = c_2/f\). Así, si una onda periódica pasa de un medio más lento a otro más rápido, su longitud de onda aumentará, y si pasa de una más rápida a otra más lenta, la longitud de onda disminuirá.
Es fácil ver físicamente por qué sucede esto, y cómo tiene que ser el caso incluso para ondas no periódicas, es decir, pulsos de onda: un pulso que entra en un medio más rápido se ensanchará en longitud (estiramiento), mientras que un pulso que entra en un medio más lento se volverá más estrecho (exprimido). Imagínese, por ejemplo, varias personas caminando en fila, separadas por la misma distancia\(d\), todas al mismo ritmo, hasta llegar a una línea más allá de la cual se supone que deben comenzar a correr. Cuando la primera persona llega a la línea, empieza a correr, pero la segunda sigue caminando, así que para cuando la segunda llega a la línea la primera ha aumentado su distancia con respecto a la segunda. Lo mismo sucederá entre el segundo y el tercero, y así sucesivamente: el “manojo” original se extenderá. (Si miras carreras de autos, ¡es probable que ya hayas visto pasar este tipo de cosas!)
Además de configurar una onda transmitida, con las propiedades que acabo de discutir, la onda incidente casi siempre hará que una onda reflejada comience a viajar en el primer medio, moviéndose hacia atrás desde el límite. La onda reflejada también tiene la misma frecuencia que la incidente, y como está viajando en el mismo medio, también tendrá la misma longitud de onda. Un pulso no periódico, cuando se refleja, por lo tanto no se estirará ni se exprimirá, sino que se “dará la vuelta” de atrás a frente, ya que la primera parte para llegar al límite también tiene que ser la primera en salir. Consulte la Figura\(\PageIndex{4}\) (la parte superior) para ver un ejemplo.
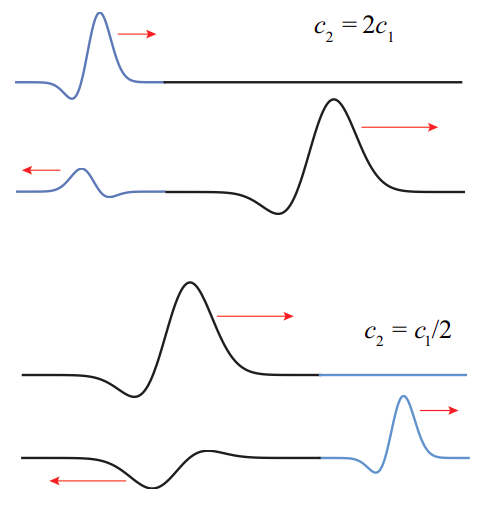
¿Cuál es la razón física de la onda reflejada? En última instancia, tiene que ver con la energía transportada por la onda incidente, y si es posible que la onda transmitida por sí sola maneje el flujo de energía entrante o no. Como vimos anteriormente (Ecuación (\ ref {eq:12.8}), la energía por unidad de volumen en una onda armónica de frecuencia angular\(\omega\) y amplitud\(\xi_0\) es\(E/V = \frac{1}{2} \rho_{0}\omega^{2}\xi^{2}_{0}\). Si la ola viaja a una velocidad\(c\), entonces el flujo de energía (energía transportada por unidad de tiempo por unidad de área) es igual a\((E/V )c\), es decir
\[ I=\frac{1}{2} c \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.14} .\]
A esto se le suele llamar la intensidad de la ola. Se puede escribir como\(I=\frac{1}{2} Z \omega^{2} \xi_{0}^{2}\), donde he definido la impedancia mecánica del medio (o simplemente la impedancia) como
\[ Z = c \rho_{0} \label{eq:12.15} \]
(para una cuerda, se\(\rho_0\) debe usar la masa por unidad de longitud\(\mu\) en lugar de la masa por unidad de volumen). Se puede ver que si los dos medios tienen la misma impedancia, entonces el flujo de energía en el medio 2 coincidirá exactamente con el del medio 1, siempre que las ondas incidente y transmitidas tengan las mismas amplitudes. En ese caso, no habrá onda reflejada: aunque los dos medios tengan diferentes densidades y velocidades de onda, siempre y cuando tengan la misma impedancia, la onda se transmitirá completamente.
Por otro lado, si los medios tienen diferentes impedancias, entonces en general será imposible igualar el flujo de energía con solo una onda transmitida, y se producirá la reflexión. Esto no es inmediatamente obvio, ya que parece que todo lo que tienes que hacer, para compensar las diferentes impedancias en la Ecuación (\ ref {eq:12.14}), es darle a la onda transmitida una amplitud que sea diferente a la de la onda incidente. Pero el punto es precisamente que, matemáticamente, no se puede hacer eso sin introducir una onda reflejada. Esto se debe a que la amplitud real de la oscilación en el límite tiene que ser la misma en ambos lados, ya que los dos medios están conectados ahí, y oscilando entre sí; así, si va a ser diferente de\(\xi_{0, \text { trans }}\),\(\xi_{0, \text { inc }}\) es necesario tener otra onda en medio 1, la onda reflejada, para asegurar eso\(\xi_{0, \text { inc }}+\xi_{0, \text { refl }}=\xi_{0, \text { trans }}\).
Otra forma de ver esto es profundizar un poco más en el significado físico de la impedancia. Este es un desvío que vale la pena, porque la impedancia en diversas formas se repite en una serie de problemas de física e ingeniería. Para una onda de sonido en un sólido, por ejemplo, podemos ver desde Eqs. (\ ref {eq:12.13}) y (\ ref {eq:12.15}) eso\(Z = c\rho_0 = \sqrt{Y \rho_0}\); así que un medio puede tener una impedancia grande ya sea por ser muy rígido (grande\(Y\)) o muy denso (grande\(\rho_0\)) o ambos; de cualquier manera, uno tendría que trabajar más duro para configurar una onda en tal medio que en uno con una impedancia menor. Por otro lado, una vez que se configura la onda, todo ese trabajo se almacena como energía de la ola, por lo que una onda en un medio con mayor también\(Z\) transportará una mayor cantidad de energía (como también se desprende de la Ecuación (\ ref {eq:12.14}) 2 para un desplazamiento dado\(\xi_0\).
Entonces, cuando una onda está tratando de pasar de un medio de baja impedancia a un medio de gran impedancia, le resultará difícil configurar una onda transmitida: la amplitud de onda transmitida será pequeña (comparada con la de la onda incidente), y la única manera de satisfacer la condición\(\xi_{0, \text { inc }}+\xi_{0, \text { refl }}=\xi_{0, \text { trans }}\) será configurar una onda reflejada con un amplitud negativa 3 —en efecto, para voltear la onda reflejada boca abajo, además de izquierda a derecha. Este es el caso ilustrado en el dibujo inferior de la Figura\(\PageIndex{4}\).
Por el contrario, se podría pensar que una onda que intenta pasar de una impedancia alta a un medio de baja impedancia no tendría problemas para establecer allí una onda transmitida, y eso es cierto, pero debido a su baja impedancia, la onda transmitida aún no podrá transportar todo el flujo de energía por sí misma. En este caso,\(\xi_{0,trans}\) será mayor que\(\xi_{0,inc}\), y esto también requerirá una onda reflejada en el primer medio, sólo que ahora estará “erguida”, es decir,\(\xi_{0, \text { refl }}=\xi_{0, \text { trans }}-\xi_{0, \text { inc }}>0\).
Para terminar el tema de la impedancia, tenga en cuenta que la observación que acabamos de hacer, esa impedancia irá típicamente como la raíz cuadrada del producto de la “rigidez” del medio multiplicada por su densidad, es bastante general. De ahí que la densidad de un medio típicamente sea un buen proxy para su impedancia, al menos siempre que el factor de “rigidez” sea independiente de la densidad (como para las cuerdas, donde es igual a la tensión) o, mejor aún, aumente con ella (como suele ser el caso de las ondas sonoras en la mayoría de los materiales). Así, a menudo escucharás que una onda reflejada es invertida (volteada boca abajo) cuando se refleja desde un medio más denso, sin ninguna referencia a la impedancia; solo se entiende que “más denso” también significa “mayor impedancia” en este caso. También tenga en cuenta, a lo largo de estas líneas, que un “extremo fijo”, como el extremo de una cuerda que está atada (o, para las ondas sonoras, el extremo cerrado de una tubería de órgano), es esencialmente equivalente a un medio con impedancia “infinita”, en cuyo caso no hay onda transmitida en ese extremo, y toda la energía se refleja.
Por último, la expresión\(\xi_{0,inc} + \xi_{0,refl}\) que escribí anteriormente, para la amplitud de la onda en el primer medio, asume implícitamente una propiedad muy importante de las ondas, que es el fenómeno conocido como interferencia, o equivalentemente, el “principio de superposición lineal”. Según este principio, cuando dos ondas se superponen en una misma región del espacio, el desplazamiento total es igual a la suma algebraica de los desplazamientos producidos por cada onda por separado. Dado que los desplazamientos se agregan con sus signos, se puede obtener interferencia destructiva si los signos son diferentes, o interferencia constructiva si los signos son los mismos. Esto jugará un papel importante en un momento, cuando iniciemos el estudio de las ondas estacionarias.
2 En este sentido, puede ayudarte pensar en la impedancia de un medio extendido como algo análoga a la inercia (masa) de una sola partícula. Cuanto mayor es la masa, más difícil es acelerar una partícula, pero una vez que le has dado una velocidad v, la masa más grande también lleva más energía.
3 Una mejor manera de poner esto sería decir que la amplitud es positiva como siempre, pero la onda reflejada está 180\(^{\circ}\) desfasada con la onda incidente, por lo que la amplitud de la onda total en el lado medio 1 del límite es\(\xi_{0,inc} − \xi_{0,refl}\).


