12.2: Ondas estacionarias y resonancia

Imagina que tienes una onda sinusoidal viajera de la forma (12.1.5), solo viajando hacia la izquierda, incidente desde la derecha sobre un “extremo fijo” a\(x\) = 0. La ola incidente irá como\(\xi_{0} \sin [2 \pi(x+c t) / \lambda]\); la onda reflejada debe voltearse de izquierda a derecha y boca abajo, así que cambie\(x\) a\(−x\) y ponga un signo menos general en el desplazamiento, para obtener\(-\xi_{0} \sin [2 \pi(-x+c t) / \lambda]\). La suma de las dos olas en la región\(x > 0\) es entonces

\[ \xi(x, t)=\xi_{0} \sin \left[\frac{2 \pi}{\lambda}(x+c t)\right]-\xi_{0} \sin \left[\frac{2 \pi}{\lambda}(-x+c t)\right]=2 \xi_{0} \sin \left(\frac{2 \pi x}{\lambda}\right) \cos (2 \pi f t) \label{eq:12.16} \]

utilizando una identidad trigonométrica para\(\sin(a + b)\), y\(f = c/\lambda\).

El resultado en el lado derecho de la Ecuación (\ ref {eq:12.16}) se llama onda estacionaria. No viaja a ningún lado, simplemente oscila “in place”: cada punto x se comporta como un oscilador separado con una amplitud\(2 \xi_{0} \sin (2 \pi x / \lambda)\). Esta amplitud es cero en puntos especiales, donde\(2x/\lambda\) es igual a un entero. Estos puntos se llaman nodos.

Podríamos pensar en “confinar” una onda de este tipo a una cadena fija en ambos extremos, si hacemos que la cadena tenga un final en\(x\) = 0 y la otra en uno de estos puntos donde la amplitud es cero; esto significa que queremos que la longitud\(L\) de la cadena satisfaga

\[ 2L = n \lambda \label{eq:12.17} \]

donde\(n\) = 1, 2,... Alternativamente, podemos pensar en ser fijos y Ecuación (\ ref {eq:12.17}) como dándonos los posibles valores de\(\lambda\) eso nos dará ondas estacionarias:\(\lambda = 2L/n\).\(L\) Ya que\(f = c/\lambda\), vemos que todas estas posibles ondas estacionarias, para fijas\(L\) y\(c\), tienen diferentes frecuencias que podemos escribir como

\[ f_{n}=\frac{n c}{2 L}, \quad n=1,2,3, \ldots \label{eq:12.18} .\]

Tenga en cuenta que estos son todos múltiplos de la frecuencia\(f_1 = c/2L\). A esto lo llamamos la frecuencia fundamental de oscilación de una cuerda fijada en ambos extremos. El periodo correspondiente a esta frecuencia fundamental es el tiempo de ida y vuelta de un pulso de onda alrededor de la cadena,\(2L/c\).

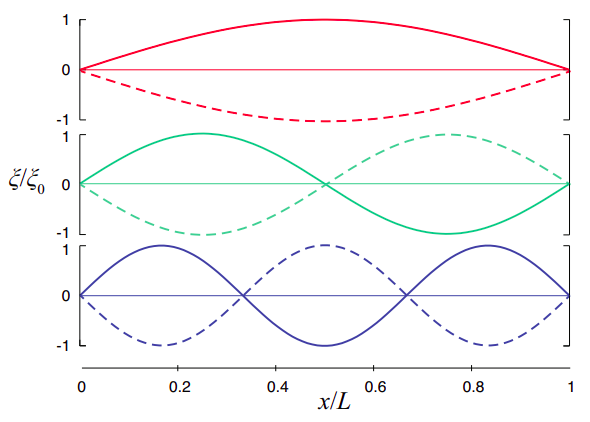
Las tres primeras ondas estacionarias se trazan en la Figura\(\PageIndex{1}\). Sus funciones de onda están dadas por el lado derecho de la Ecuación (\ ref {eq:12.16}), para 0\(x\) ≤ ≤\(L\), con\(\lambda = 2L/n\) (\(n\)= 1, 2, 3), y\(f = f_n = nc/2L\). La amplitud es arbitraria; en la figura la he ajustado igual a 1 por conveniencia. Llamar a la función correspondiente\(u_n(x, t)\) es una práctica más o menos común en otros contextos:

\[ u_{n}(x, t)=\sin \left(\frac{n \pi x}{L}\right) \cos \left(2 \pi f_{n} t\right) \label{eq:12.19} .\]

Estas funciones se denominan los modos normales de vibración de la cuerda. En la Figura\(\PageIndex{1}\) I se ha mostrado, para cada una de ellas, el desplazamiento en el tiempo inicial,\(t\) = 0, como una línea continua, y luego medio periodo después como una línea discontinua. Además de esto, observe que la función de onda se desvanece de manera idéntica (la cadena es plana) en los intervalos de un cuarto de período,\(t = 1/4f_n\) y\(t = 3/4f_n\). En esos momentos, la onda no tiene energía potencial elástica (ya que la cuerda está sin estirar): como con un simple oscilador que pasa por la posición de equilibrio, toda su energía es cinética. Porque\(n > 1\), también hay nodos (lugares donde la amplitud de oscilación es siempre cero) en puntos distintos a los extremos. Incluyendo los puntos finales, el modo normal\(n\) -ésimo tiene\(n + 1\) nodos. Los lugares donde la amplitud de oscilación es mayor se denominan antinodos.

Figura\(\PageIndex{1}\): Los tres modos normales de vibración de frecuencia más baja de una cuerda sujeta en ambos extremos, correspondientes a, de arriba a abajo,\(n\) = 1, 2, 3

Las animaciones de estas ondas estacionarias se pueden encontrar en muchos lugares; una que me gusta particularmente está aquí: http://newt.phys.unsw.edu.au/jw/strings.html#standing. También muestra gráficamente cómo la onda estacionaria puede considerarse como una superposición de dos ondas viajeras de dirección opuesta, como en la Ecuación (\ ref {eq:12.16}).

Si inicialmente doblamos la cuerda en una de las formas que se muestran en la Figura\(\PageIndex{1}\), y luego la soltamos, oscilaría a la frecuencia correspondiente\(f_n\), manteniendo la misma forma, solo escalándola hacia arriba y hacia abajo por un factor a\(\cos(2\pi f_{n}t)\) medida que transcurra el tiempo. Entonces, otra forma de pensar en las ondas estacionarias es como los modos naturales de vibración de un sistema extendido —la cuerda, en este caso, aunque las ondas estacionarias se pueden producir en cualquier medio que pueda llevar una onda viajera.

Lo que quiero decir con un “modo natural de vibración” es lo siguiente: un solo oscilador, digamos, un péndulo, tiene una sola frecuencia “natural”; si lo desplazas o lo golpeas, simplemente oscila a esa frecuencia con una amplitud constante. Un sistema extendido, como la cadena, puede ser visto como una colección de osciladores acoplados, que en general pueden oscilar de muchas maneras diferentes y complicadas; sin embargo, hay un conjunto específico de frecuencias —para la cadena con dos extremos fijos, la secuencia\(f_n\) de Ecuación (\ ref {eq:12.18}) —y asociada formas que darán como resultado que todas las partes de la cuerda realicen movimientos armónicos simples, en sincronía, todo a la misma frecuencia.

Por supuesto, para producir solo uno de estos modos específicos de oscilación requiere cierto cuidado (“conducir” la cuerda a la frecuencia correcta es probablemente la forma más fácil; ver párrafo siguiente); sin embargo, si simplemente golpeas o arrancas la cuerda de alguna manera aleatoria, sucede algo notable: el movimiento resultante será, matemáticamente, descrito como una suma de ondas estacionarias sinusoidales, cada una con una de las frecuencias\(f_n\), y cada una con una amplitud diferente\(A_n\). En un instrumento musical, esto eventualmente generará una superposición de ondas sonoras con frecuencias\(f_1 = c/2L\),\(f_2 = 2f_1\),\(f_3 = 3f_1\)... (llamado, en este contexto, lo fundamental,\(f_1\), y sus connotaciones,\(f_n = nf_1\)). Cada una de estas frecuencias corresponde a un tono diferente, o nota musical, y el resultado sonará un poco como un acorde, aunque no tan pronunciado; en su mayoría escucharemos solo lo fundamental, que corresponde a la nota raíz del acorde, pero todas las notas de una tríada mayor están de hecho presentes en la vibración de una sola cuerda de guitarra o piano ⁴.

Pero espera, ¡hay más! Supongamos que intentas que la cuerda oscile “conduciéndola”: es decir, agarrando una sujeción de un extremo y agitándola a alguna frecuencia, sólo con una amplitud muy pequeña, por lo que el desplazamiento en ese extremo permanece siempre cerca de cero. En ese caso, normalmente obtendrá solo oscilaciones de amplitud muy pequeñas, hasta que la frecuencia de conducción alcance una de las frecuencias especiales\(f_n\), momento en el que obtendrá una gran oscilación con la forma de la onda estacionaria correspondiente. Este es un fenómeno conocido como resonancia, y las\(f_n\) son las frecuencias resonantes de este sistema.

Tenga en cuenta que el efecto que acabo de describir es esencialmente el mismo que experimenta cuando está “bombeando”, o simplemente empujando, un columpio. A menos que lo hagas a la frecuencia correcta, no llegas muy lejos; pero si lo haces a la frecuencia correcta (que es la frecuencia natural del swing, aquella a la que oscilará por sí sola), puedes obtener enormes oscilaciones de amplitud. Entonces, se puede decir que las frecuencias (\ ref {eq:12.18}) son las frecuencias de oscilación natural de la cadena de las mismas dos maneras: son las que oscilará si simplemente la arrancas, y son las que tienes que conducirla si quieres obtener grandes oscilaciones.

Prácticamente todo lo que te acabo de mostrar arriba para ondas estacionarias en una cuerda se aplica a las ondas sonoras dentro de un tubo o tubería abierta en ambos extremos. En ese caso, sin embargo, no es el desplazamiento, sino la onda de presión (o densidad) la que debe tener ceros en los extremos (ya que los extremos están abiertos, la presión debe haber solo la presión atmosférica promedio; tenga en cuenta que las ondas de presión o densidad en una onda sonora no dan la presión o densidad absolutas, pero la desviación, positiva o negativa, de la media). La matemática, sin embargo, es idéntica, y se encuentra el mismo conjunto de modos normales y frecuencias de resonancia que el anterior. Estas son entonces las frecuencias que se producirían al soplar en una flauta o un tubo de órgano abierto en ambos extremos. Entonces, tanto de pipas como de cuerdas obtenemos la misma “serie armónica” de frecuencias (\ ref {eq:12.18}) que ha sido la base de la música occidental desde al menos la época de Pitágoras.

---

⁴ Funciona así: digamos\(f_1\) corresponde a una C, entonces\(f_2\) es la C por encima de eso,\(f_3\) la G por encima de eso,\(f_4\) la C por encima de eso, y\(f_5\) la E por encima de eso.