13.2: Introducción de la temperatura
- Page ID
- 128069
Capacidad de temperatura y calor
El cambio de perspectiva que acabo de mencionar también significa que no es fácil ni siquiera definir la temperatura, más allá de nuestra intuición natural de “caliente” y “frío”, o la noción algo circular de que la temperatura es simplemente “lo que miden los termómetros”. En términos generales, sin embargo, la temperatura es una medida de la cantidad (o, para ser algo más precisos, la concentración) de energía térmica en un objeto. Cuando ponemos directamente una cantidad de energía térmica,\(\Delta E_{th}\) (lo que vamos a llamar calor en un momento), en un objeto, normalmente observamos su temperatura para aumentar de una manera que es aproximadamente proporcional a\(\Delta E_{th}\), al menos mientras no\(\Delta E_{th}\) sea demasiado grande:
\[ \Delta T=\frac{\Delta E_{t h}}{C} \label{eq:13.1} .\]
La constante de proporcionalidad\(C\) se llama la capacidad calorífica del objeto: de acuerdo con la Ecuación (\ ref {eq:13.1}), un sistema con una gran capacidad calorífica podría absorber (o emitir, se supone que la ecuación se aplica en cualquier caso) una gran cantidad de energía térmica sin experimentar una gran cambio de temperatura. Si el sistema no realiza ningún trabajo en el proceso (¡recuerde la Ecuación (7.4.8)!) , entonces su energía interna aumentará (o disminuirá) exactamente la misma cantidad de energía térmica que ha absorbido (o emitido) 1, y podemos usar la capacidad calorífica 2 para, en última instancia, relacionar la temperatura del sistema con su contenido de energía de una a una sola vía.
Lo que se encuentra experimentalmente es que la capacidad calorífica de un objeto homogéneo (es decir, uno hecho de una sola sustancia) es, en general, proporcional a su masa. Es por ello que, en lugar de tablas de capacidades térmicas, lo que compilamos son tablas de calores específicos, que son capacidades térmicas por kilogramo (o a veces por mol, o por centímetro cúbico... pero todas estas cosas son en última instancia proporcionales a la masa del objeto). En términos de un calor específico\(c = C/m\), y de nuevo asumiendo que no hay trabajo realizado o por el sistema, podemos reescribir la Ecuación (\ ref {eq:13.1}) para leer
\[ \Delta E_{s y s}=m c \Delta T \label{eq:13.2} \]
o, de nuevo,
\[ \Delta T=\frac{\Delta E_{s y s}}{m c} \label{eq:13.3} \]
lo que demuestra lo que dije anteriormente, que la temperatura realmente mide, no el contenido energético total de un objeto, sino su concentración —la energía térmica “por unidad de masa”, o, si se prefiere (y algo más fundamentalmente) “por molécula”. Un objeto puede tener una gran cantidad de energía térmica solo en virtud de ser enorme, y aún así estar bastante frío (el agua en el océano es un buen ejemplo).
De hecho, también podemos reescribir Eqs. (\ ref {eq:13.1} —\ ref {eq:13.3}) en la forma (algo ideada)
\[ C=m c=m \frac{\Delta E_{s y s} / m}{\Delta T} \label{eq:13.4} \]
que te dice que un objeto puede tener una gran capacidad calorífica de dos maneras: una es simplemente tener mucha masa, y la otra es tener un calor específico grande. La primera de estas formas es algo aburrida (pero potencialmente útil, como discutiré más adelante); la segunda es interesante, porque significa que un cambio relativamente grande en la energía interna por molécula (en términos generales, el numerador de (\ ref {eq:13.4})) solo se mostrará como un cambio relativamente pequeño en temperatura (el denominador de (\ ref {eq:13.4}); un numerador grande y un denominador pequeño hacen para una fracción grande!).
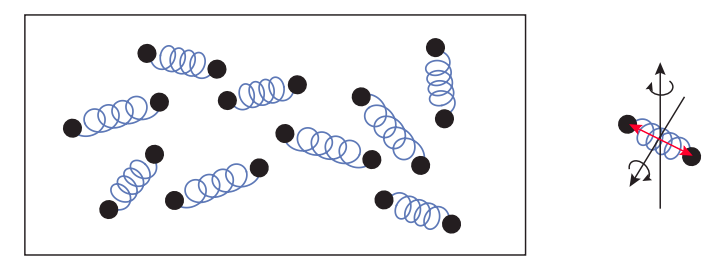
Dicho de otra manera, y algo fantasiosamente, las sustancias con un gran calor específico son muy buenas para ocultar su energía térmica de los termómetros (ver Figura\(\PageIndex{1}\) para un ejemplo). Esto, como dije, es una observación interesante, pero también significa que medir las capacidades de calor —o, para el caso, medir la temperatura en sí misma— puede no ser un asunto fácil. ¿Cómo obtenemos la energía interna del objeto si no a través de su temperatura? ¿Por dónde empieza uno?
1 Si el sistema hace algún trabajo (o ha trabajado en él), entonces aplica la Ecuación (13.3.1).
2 Lo cual, debe señalarse, también puede ser una función de la temperatura del sistema, otra complicación que alegremente ignoraremos aquí.
El termómetro de gas
Un buen comienzo, al menos conceptualmente, se proporciona al mirar un sistema que no tiene lugar para ocultar su energía térmica, tiene que mostrarlo todo, tenerlo, por así decirlo, a la vista todo el tiempo. Tal sistema es lo que ha llegado a ser conocido como un gas ideal —que modelamos, microscópicamente, como una colección de moléculas (o, más propiamente, átomos) sin dimensión ni estructura: simplemente cosas puntuales zumbando y golpeando continuamente entre sí y contra las paredes de sus contenedor. Para tal sistema, el único tipo posible de energía interna es la suma de la energía cinética traslacional de las moléculas. Podemos esperar que esto sea fácilmente detectado por un termómetro (o cualquier otra sonda sensible a la energía), ya que a medida que las moléculas de gas chocan contra el termómetro, revelarán indirectamente la energía que transportan, tanto por la frecuencia como por la fuerza que chocan.
Resulta que podemos ser mucho más precisos que eso. Podemos analizar el modelo teórico de un gas ideal que acabamos de describir con bastante facilidad, utilizando nada más que los conceptos que hemos introducido anteriormente en el semestre (más algunas ideas estadísticas simples) y obtener el siguiente resultado para la presión y el volumen del gas:
\[ P V=\frac{2}{3} N\left\langle K_{\text {trans}}\right\rangle \label{eq:13.5} \]
donde\(N\) es el número total de moléculas, y\(\left\langle K_{\text {trans}}\right\rangle\) es la energía cinética traduccional promedio por molécula. Ahora bien, es muy probable que hayas visto, en la química de la secundaria, la “ley del gas ideal” derivada experimentalmente,
\[ P V=n R T \label{eq:13.6} \]
donde\(n\) está el número de moles, y\(R\) la “constante de gas ideal”. Comparando la ecuación (\ ref {eq:13.5}) (una predicción teórica para un modelo matemático) y la ecuación (\ ref {eq:13.6}) (un resultado empírico aproximadamente válido para muchos gases del mundo real bajo un amplio rango de presión y temperatura, donde “temperatura” significa literalmente simplemente “lo que mediría cualquier buen termómetro ”) inmediatamente nos dice qué es la temperatura, al menos para este sistema extremadamente simple: es solo una medida de la energía cinética promedio (traslacional) por molécula.
Sería tentador dejarlo así, e inmediatamente generalizar el resultado a todo tipo de otros sistemas. Después de todo, presumiblemente, un termómetro insertado en un líquido responde fundamentalmente a lo mismo que un termómetro insertado en un gas ideal: es decir, a la frecuencia y la dureza de las moléculas del líquido golpean contra la pared del termómetro. Entonces podemos suponer que, de hecho, debe estar midiendo lo mismo en ambos casos y esa sería la energía cinética traduccional promedio por molécula. En efecto, hay un resultado en la mecánica estadística clásica que establece que para cualquier sistema (líquido, sólido o gaseoso) en “equilibrio térmico” (un estado que definiré más precisamente más adelante), la energía cinética traduccional promedio por molécula debe ser
\[ \left\langle K_{\text {trans}}\right\rangle=\frac{3}{2} k_{B} T \label{eq:13.7} \]
donde\(k_B\) es una constante llamada constante de Boltzmann (\(k_B\)= 1.38×10 −23 J/K), y\(T\), como en la Ecuación (\ ref {eq:13.6}) se mide en grados Kelvin.
No hay nada malo en esta forma de pensar sobre la temperatura, salvo que es demasiado autolimitante. Simplemente identificar la temperatura con la energía cinética traduccional por molécula deja fuera muchos otros tipos posibles de energía que un sistema complejo podría tener (una molécula suficientemente compleja también puede rotar y vibrar, por ejemplo, como se muestra en la Figura\(\PageIndex{1}\); estas son algunas de las formas en que la molécula puede “ocultar” su energía del termómetro, como sugerí anteriormente). Normalmente, todas esas otras formas de energía interna también suben a medida que aumenta la temperatura, por lo que sería al menos un poco engañoso pensar que la temperatura tiene que ver solo con\(K_{trans}\), a pesar de la Ecuación (\ ref {eq:13.7}). En definitiva, de hecho, es la energía interna total del sistema la que queremos relacionar con la temperatura, lo que significa tener que lidiar con esos molestos calores específicos que introduje en el apartado anterior. (Como un aparte, el cálculo de calores específicos fue uno de los grandes desafíos para los físicos teóricos de finales del siglo XIX y principios del XX, y finalmente condujo a la introducción de la mecánica cuántica, ¡pero esa es otra historia!)
En cualquier caso, el gas ideal no sólo nos proporciona una visión de la imagen microscópica detrás del concepto de temperatura, también puede servir como termómetro en sí. La ecuación (\ ref {eq:13.6}) muestra que el volumen de un gas ideal mantenido a presión constante aumentará de una manera que es directamente proporcional a la temperatura. Así es como funcionaba un termómetro de mercurio convencional y anticuado, a medida que aumentaba la temperatura, el volumen del líquido en el tubo aumentaba. El termómetro de gas ideal es un poco más engorroso (un cambio de temperatura relativamente pequeño puede causar un cambio de volumen bastante grande), pero, como dije anteriormente, normalmente funciona bien en un rango de temperatura muy grande.
Al usar un gas ideal (o casi ideal) como termómetro, basado en la Ecuación (\ ref {eq:13.6}), estamos, de hecho, definiendo implícitamente una escala de temperatura específica, la escala Kelvin (de hecho, puede recordar que para que la Ecuación (\ ref {eq:13.6}) funcione, la temperatura debe medirse en grados Kelvin). El punto cero de esa escala (lo que llamamos cero absoluto) es el punto teórico en el que un gas ideal se encogería precisamente a volumen cero. Por supuesto, ningún gas se queda ideal (¡ni siquiera gaseoso!) a temperaturas tan bajas, pero el punto se puede encontrar fácilmente por extrapolación: por ejemplo, imagine trazar valores experimentales de\(V\) vs\(T\), a presión constante, para un gas casi ideal, usando cualquier tipo de escala de termómetro para medir\(T\), en un amplio rango de temperaturas. Luego, conecta los puntos por una línea recta, y extiende la línea hasta donde cruza el\(T\) eje (así\(V\) = 0); ese punto te da el valor de cero absoluto en la escala que estabas usando, como −273.15 Celsius, por ejemplo, o −459.67 Fahrenheit.
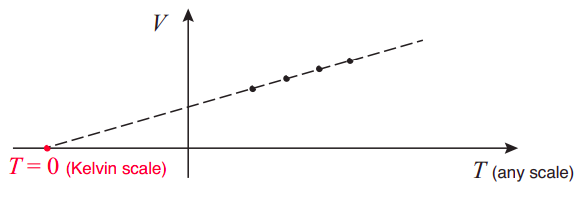
La conexión entre la temperatura Kelvin (o absoluta) y el movimiento microscópico expresado por ecuaciones como (\ ref {eq:13.5}) a través de (\ ref {eq:13.7}) inmediatamente nos dice que a medida que bajes la temperatura los átomos en tu sistema se moverán cada vez más lentamente, hasta que, cuando alcances el cero absoluto, todos cesaría el movimiento microscópico. Esto no sucede del todo, debido a la mecánica cuántica, y también creemos que es imposible alcanzar realmente el cero absoluto por otras razones, pero es cierto a una muy buena aproximación, y los experimentalistas recientemente se han vuelto muy buenos para enfriar pequeños conjuntos de átomos a temperaturas extremadamente cercanas a cero absoluto, donde los átomos se mueven, literalmente, más lentos que los caracoles (en lugar de pasar zumbando cerca de la velocidad del sonido, como lo hacen las moléculas de aire a temperatura ambiente).
La Ley Cero
Históricamente, los termómetros se volvieron útiles porque nos dieron una forma de cuantificar nuestra percepción natural de frío y calor, pero la cantidad que miden, la temperatura, habría sido bastante inútil si no hubiera exhibido una propiedad importante, que naturalmente damos por sentada, pero que es, de hecho, sorprendentemente no trivial. Esta propiedad, que suele denominarse la ley cero-ésima de la termodinámica, se puede afirmar de la siguiente manera:
Supongamos que coloca dos sistemas\(A\) y\(B\) en contacto, para que puedan intercambiar directamente la energía térmica (más sobre esto en la siguiente sección), a la vez que los aíslan del resto del mundo (por lo que su energía térmica conjunta no tiene otro lugar a donde ir). Entonces, eventualmente, alcanzarán un estado, llamado equilibrio térmico, en el que ambos tendrán la misma temperatura.
Esto es importante por muchas razones, entre las cuales no menos importante es que eso es lo que nos permite medir la temperatura con un termómetro en primer lugar: el termómetro nos dice la temperatura del objeto con el que lo colocamos en contacto, ¡al adoptar primero esa temperatura! Por supuesto, se tiene que diseñar un buen termómetro para que lo haga mientras cambia la temperatura del sistema siendo medida lo menos posible; es decir, el termómetro tiene que tener una capacidad calorífica mucho menor que la del sistema que está midiendo, de manera que solo necesita dar o tomar una muy pequeña cantidad de energía térmica con el fin de igualar su temperatura. Pero el punto principal aquí es que el partido realmente ocurre, y cuando lo haga, la temperatura medida por el termómetro será la misma para cualquier otro sistema que esté, a su vez, en equilibrio térmico con—es decir, a la misma temperatura que el primero.
La ley cero-ésima sólo nos asegura que el equilibrio térmico eventualmente sucederá, es decir, los dos sistemas eventualmente alcanzarán una y la misma temperatura; no nos dice cuánto tiempo puede tardar esto, ni siquiera, por sí mismo, cuál será esa temperatura final. Este último punto, sin embargo, se puede determinar fácilmente si se hace uso de la conservación de la energía (¡la primera ley, que viene!) y el concepto de capacidad calorífica introducido anteriormente (piénsalo por un minuto).
Aún así, como dije anteriormente, este resultado está lejos de ser trivial. Imagínese, por ejemplo, dos gases ideales diferentes, cuyas moléculas tienen diferentes masas, que llevan a un estado de equilibrio térmico conjunto. Las ecuaciones (\ ref {eq:13.5}) a (\ ref {eq:13.7}) nos dicen que en este estado final la energía cinética traduccional promedio de las “\(A\)” moléculas y las “\(B\)” moléculas será la misma. Esto significa, en particular, que las moléculas más masivas terminarán moviéndose más lentamente, en promedio, así\(m_av^2_{a,av} = m_bv^2_{b,av}\). Pero, ¿por qué es eso? ¿Por qué deberían ser las energías cinéticas las que terminan igualando, en promedio, y no, digamos, el momento, o las velocidades moleculares mismas? El resultado, aunque indudablemente cierto, desafió una prueba matemática rigurosa durante décadas, si no siglos; no estoy seguro de que exista una prueba rigurosa, incluso ahora mismo.


