4.4: Movimiento circular

A menudo consideramos el movimiento de un objeto alrededor de un círculo de radio fijo,\(R\). En principio, esto es movimiento en dos dimensiones, ya que un círculo está necesariamente en un plano bidimensional. Sin embargo, dado que el objeto está limitado a moverse a lo largo de la circunferencia del círculo, puede pensarse (y tratarse como) movimiento a lo largo de un eje unidimensional que es curvo.

Figura\(\PageIndex{1}\): Describiendo el movimiento de un objeto alrededor de un círculo de radio\(R\).

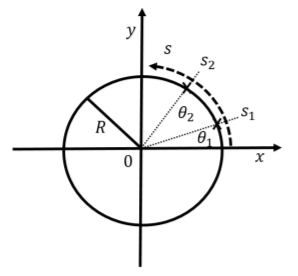
La figura\(\PageIndex{1}\) muestra cómo podemos describir el movimiento a lo largo de un círculo de radio,\(R\). Podríamos usar\(x(t)\) y\(y(t)\) describir la posición en el círculo, sin embargo,\(x(t)\) y ya no\(y(t)\) son independientes ya que tienen que corresponder a las coordenadas de puntos en un círculo:

\[\begin{aligned} x^2(t)+y^2(t)=R^2\end{aligned}\]

En lugar de usar\(x\) y\(y\), podríamos pensar en un eje que se dobla alrededor del círculo (como lo muestra la flecha curva en la Figura\(\PageIndex{1}\), el\(s\) eje). El\(s\) eje es tal que\(s=0\) donde el círculo se cruza con el\(x\) eje, y el valor de\(s\) aumenta a medida que nos movemos en sentido antihorario a lo largo del círculo. La distancia a lo largo\(s\) del eje corresponde así a la distancia a lo largo de la circunferencia del círculo.

Otra variable que podría utilizarse para la posición en lugar de\(s\) es el ángulo,\(\theta\), entre el vector de posición del objeto y el\(x\) eje, como se ilustra en la Figura\(\PageIndex{1}\). Si expresamos el ángulo\(\theta\) en radianes, entonces es fácil convertir entre\(s\) y\(\theta\). Recordemos, un ángulo en radianes se define como la longitud de un arco subtendido por ese ángulo dividido por el radio del círculo. Así tenemos:

\[\theta(t)=\frac{s(t)}{R}\]

En particular, si el objeto ha dado la vuelta a todo el círculo, entonces\(s=2\pi R\) (la circunferencia de un círculo), y el ángulo correspondiente es, a saber\(\theta=\frac{2\pi R}{R}=2\pi\), 360.

Al usar el ángulo,\(\theta\), en lugar de\(x\) y\(y\), estamos usando efectivamente coordenadas polares, con un radio fijo. Como ya vimos, las\(y\) posiciones\(x\) y están relacionadas\(\theta\) por:

\[\begin{aligned} x(t) &= R\cos(\theta(t))\\ y(t) &= R\sin(\theta(t))\\\end{aligned}\]

donde\(R\) es una constante. Para un objeto que se mueve a lo largo del círculo, podemos escribir su vector de posición,\(\vec r(t)\), como:

\[\begin{aligned} \vec r(t)&= \begin{pmatrix} x(t) \\ y(t) \\ \end{pmatrix} =R \begin{pmatrix} \cos(\theta(t)) \\ \sin(\theta(t)) \\ \end{pmatrix}\end{aligned}\]

y así el vector de velocidad viene dado por:

\[\begin{aligned} \vec v(t) &=\frac{d}{dt}\vec r(t) =\frac{d}{dt} R \begin{pmatrix} \cos(\theta(t)) \\ \sin(\theta(t)) \\ \end{pmatrix} \\ &= R \begin{pmatrix} \frac{d}{dt}\cos(\theta(t)) \\ \frac{d}{dt}\sin(\theta(t)) \\ \end{pmatrix} \\ &= R \begin{pmatrix} -\sin(\theta(t))\frac{d\theta}{dt} \\ \cos(\theta(t))\frac{d\theta}{dt} \\ \end{pmatrix} \\ \end{aligned}\]

donde se utilizó la Regla de Cadena para calcular las derivadas de tiempo de las funciones trigonométricas (ya que\(\theta(t)\) es función del tiempo). Podemos escribir esto en forma de componentes:

\[v_x = -R\sin(\theta(t))\frac{d\theta}{dt}\]

\[ v_y = R\cos(\theta(t))\frac{d\theta}{dt}\]

La magnitud del vector de velocidad viene dada por:

\[\begin{aligned} ||\vec v|| &=\sqrt{ v_x^2+v_y^2}\\ &=\sqrt{ \left(-R\sin(\theta(t))\frac{d\theta}{dt}\right)^2+\left(R\cos(\theta(t))\frac{d\theta}{dt}\right)^2}\\ &=\sqrt{ R^2\left( \frac{d\theta}{dt}\right)^2[\sin^2(\theta(t))+\cos^2(\theta(t)]}\\ &=R\left |\frac{d\theta}{dt}\right|\end{aligned}\]

Los vectores de posición y velocidad se ilustran en la Figura\(\PageIndex{2}\) para un ángulo\(\theta\) en el primer cuadrante (\(0<\theta<\frac{\pi}{2}\)).

Figura\(\PageIndex{2}\): El vector de posición,\(\vec r(t)\) es siempre perpendicular al vector de velocidad,\(\vec v(t)\), para el movimiento en un círculo.

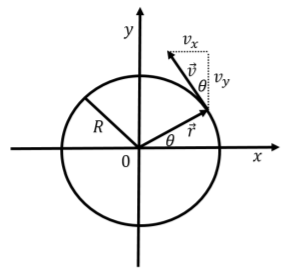
En este caso, se puede observar que el\(x\) componente de la velocidad es negativo (del diagrama y de la Ecuación 4.4.2). De las Ecuaciones 4.4.2 y 4.4.3, también se puede ver eso\(\frac{|v_x|}{|v_y|}=\tan(\theta)\), que se ilustra en la Figura\(\PageIndex{2}\), mostrando que el vector de velocidad es tangente al círculo y perpendicular al vector de posición. Este es siempre el caso del movimiento a lo largo de un círculo.

Podemos simplificar nuestra descripción del movimiento a lo largo del círculo usando cualquiera\(s(t)\) o\(\theta(t)\) en lugar de los vectores para la posición y la velocidad. Si usamos\(s(t)\) para representar la posición a lo largo de la circunferencia (\(s=0\)donde el círculo cruza el\(x\) eje), entonces la velocidad a lo largo del\(s\) eje es:

\[\begin{aligned} v_s(t)&=\frac{d}{dt}s(t)\\ &=\frac{d}{dt}R\theta(t)\\ &=R\frac{d\theta}{dt}\end{aligned}\]

donde utilizamos el hecho de que\(\theta=s/R\) para convertir de\(s\) a\(\theta\). La velocidad a lo largo\(s\) del eje es así precisamente igual a la magnitud del vector de velocidad bidimensional (derivado anteriormente), lo que tiene sentido ya que el vector de velocidad es tangente al círculo (y por lo tanto en la\(s\) “dirección”).

Si el objeto tiene una velocidad constante,\(v_s\), a lo largo del círculo y comenzó en una posición a lo largo de la circunferencia\(s=s_0\), entonces su posición a lo largo del\(s\) eje se puede describir usando cinemática 1D:

\[\begin{aligned} s(t)=s_0+v_st\end{aligned}\]

o, en términos de\(\theta\):

\[\begin{aligned} \theta(t)&=\frac{s(t)}{R}=\frac{s_0}{R}+\frac{v_s}{R}t\\ &=\theta_0 + \frac{d\theta}{dt}t\\ &=\theta_0 + \omega t \\ \therefore\omega &= \frac{d\theta}{dt}\end{aligned}\]

donde introdujimos\(\theta_0\) como el ángulo correspondiente a la posición\(s_0\), e introducimos\(\omega=\frac{d\theta}{dt}\), que es análogo a la velocidad, pero para un ángulo. \(\omega\)se llama la velocidad angular y es una medida de la velocidad de cambio del ángulo\(\theta\) (ya que es la derivada del tiempo del ángulo). La relación entre la velocidad “lineal”\(v_s\) (la magnitud del vector de velocidad, que corresponde a la velocidad en la dirección tangente al círculo) y\(\omega\) es:

\[\begin{aligned}v_s=R\frac{d\theta}{dt}=R\omega \end{aligned}\]

Del mismo modo, si el objeto está acelerando, podemos definir una aceleración angular\(\alpha(t)\),, como la velocidad de cambio de la velocidad angular:

\[\begin{aligned} \alpha(t)=\frac{d\omega}{dt}\end{aligned}\]

que puede estar directamente relacionado con la aceleración en la\(s\) dirección,\(a_s(t)\):

\[\begin{aligned} a_s(t) &= \frac{d}{dt}v_s\\ &=\frac{d}{dt}\omega R=R\frac{d\omega}{dt}\\ a_s(t)&=R\alpha \end{aligned}\]

Así, las cantidades lineales (las que están a lo largo\(s\) del eje) pueden relacionarse con las cantidades angulares multiplicando las cantidades angulares por\(R\):

\[s=R\theta\]

\[v_{s}=R\omega\]

\[a_{s}=R\alpha\]

Si el objeto comenzó en\(t=0\) con una posición\(s=s_0\) (\(\theta=\theta_0\)), y una velocidad lineal inicial\(v_{0s}\) (velocidad angular\(\omega_0\)), y tiene una aceleración lineal constante alrededor del círculo,\(a_s\) (aceleración angular,\(\alpha\)), entonces la posición del objeto se puede describir usando las cantidades lineales o angulares:\[\begin{aligned} s(t) &= s_0+v_{s0}t+\frac{1}{2}a_s t^2\\ \theta(t) &= \theta_0+\omega_0t+\frac{1}{2}\alpha t^2\end{aligned}\]

Como recuerda de la Sección 4.3, podemos calcular el vector de aceleración e identificar componentes que son paralelos y perpendiculares al vector de velocidad:

\[\begin{aligned} \vec a&=\vec a_{\parallel}(t) + \vec a_{\bot}(t)\\ &=\frac{dv}{dt}\hat v(t)+v\frac{d\hat v}{dt}\\\end{aligned}\]

El primer término,\(\vec a_{\parallel}(t)=\frac{dv}{dt}\hat v(t)\), es paralelo al vector de velocidad\(\hat v\), y tiene una magnitud dada por:

\[\begin{aligned} ||\vec a_{\parallel}(t)||&=\frac{dv}{dt}=\frac{d}{dt} v(t)=\frac{d}{dt} R\omega=R\alpha\end{aligned}\]

Es decir, el componente del vector de aceleración que es paralelo a la velocidad es precisamente la aceleración en la\(s\) dirección (la aceleración lineal). Este componente de la aceleración se encarga de aumentar (o disminuir) la velocidad del objeto y es cero si el objeto va alrededor del círculo con una velocidad constante (lineal o angular).

Como vimos anteriormente, la componente perpendicular de la aceleración,\(\vec a_{\bot}(t)\), se encarga de cambiar la dirección del vector de velocidad (ya que el objeto cambia continuamente de dirección al ir en círculo). Cuando el movimiento está alrededor de un círculo, este componente del vector de aceleración se llama aceleración “centrípeta” (es decir, aceleración apuntando hacia el centro del círculo, como veremos). Podemos calcular la aceleración centrípeta en términos de nuestras variables angulares, señalando que el vector unitario en la dirección de la velocidad es\(\hat v=-\sin(\theta)\hat x+\cos(\theta)\hat y\):

\[\begin{aligned} \vec a_{\bot}(t)&=v\frac{d\hat v}{dt}\nonumber\\ &=(\omega R)\frac{d}{dt} \left[-\sin(\theta)\hat x+\cos(\theta)\hat y\right]\nonumber\\ &=\omega R \left[-\frac{d}{dt}\sin(\theta)\hat x+\frac{d}{dt}\cos(\theta)\hat y\right]\nonumber\\ &=\omega R \left[-\cos(\theta)\frac{d\theta}{dt}\hat x-\sin(\theta)\frac{d\theta}{dt}\hat y\right]\nonumber\\ &=\omega R [-\cos(\theta)\omega\hat x-\sin(\theta)\omega\hat y]\nonumber\end{aligned}\]

\[\stackrel{\rightarrow}{a} _{\bot}(t)=ω^{2}R[-\cos(\theta)\hat x-\sin(\theta)\hat y\]

donde puede verificar fácilmente que el vector\([-\cos(\theta)\hat x-\sin(\theta)\hat y]\) tiene longitud unitaria y apunta hacia el centro del círculo (cuando la cola se coloca en un punto en el círculo en ángulo\(\theta\)). La aceleración centrípeta apunta así hacia el centro del círculo y tiene magnitud:

\[a_c(t) = ||\vec a_{\bot}(t)||=\omega^2(t) R = \frac{v^2(t)}{R}\]

donde en el último signo igual, escribimos la aceleración centrípeta en términos de la velocidad alrededor del círculo (\(v=||\vec v||=v_s\)).

Si un objeto va alrededor de un círculo, siempre tendrá una aceleración centrípeta (ya que su vector de velocidad debe cambiar de dirección). Además, si la velocidad del objeto está cambiando, también tendrá una aceleración lineal, que apunta en la misma dirección que el vector de velocidad (cambia la longitud del vector de velocidad pero no su dirección).

Ejercicio\(\PageIndex{1}\)

Una vicuña va en el sentido de las agujas del reloj alrededor de un círculo que se centra en el origen de una\(xy\) coordinate system that is in the plane of the circle. The vicuña runs faster and faster around the circle. In which direction does its acceleration vector point just as the vicuña is at the point where the circle intersects the positive \(y\) axis?

1. En la\(y\) dirección negativa.
2. En la\(y\) dirección positiva.
3. Una combinación de las\(x\) direcciones positiva\(y\) y positiva.
4. Una combinación de las\(x\) direcciones negativa\(y\) y positiva.
5. Una combinación de las\(x\) direcciones negativa\(y\) y negativa.

Contestar

Periodo y Frecuencia

Cuando un objeto se mueve en círculo, normalmente completará más de una revolución. Si el objeto va alrededor del círculo con una velocidad constante, llamamos al movimiento “movimiento circular uniforme”, y podemos definir el período y la frecuencia del movimiento.

El periodo\(T\),, se define como el tiempo que lleva completar una revolución alrededor del círculo. Si el objeto tiene velocidad angular constante\(\omega\), podemos encontrar el tiempo,\(T\), que se necesita para completar una revolución completa, de\(\theta=0\) a\(\theta=2\pi\):

\[\begin{aligned} \omega&=\frac{\Delta \theta}{T}=\frac{2\pi}{T}\nonumber\end{aligned}\]

\[T=\frac{2\pi}{\omega}\]

Obtendríamos el mismo resultado usando las cantidades lineales; en una revolución, el objeto cubre una distancia de\(2\pi R\) a una velocidad de\(v\):\[\begin{aligned} v&=\frac{2\pi R}{T}\\ T&=\frac{2\pi R}{v}=\frac{2\pi R}{\omega R}=\frac{2\pi}{\omega}\end{aligned}\]

La frecuencia\(f\),, se define como la inversa del periodo:

\[\begin{aligned} f&=\frac{1}{T}=\frac{\omega}{2\pi}\end{aligned}\]

y cuenta con unidades SI de\(\text{Hz}=\text{s}^{-1}\). Piense en la frecuencia como el número de revoluciones completadas por segundo. Así, si la frecuencia es\(f=1\text{Hz}\), el objeto va alrededor del círculo una vez por segundo. Dada la frecuencia, por supuesto podemos obtener la velocidad angular:

\[\begin{aligned} \omega = 2\pi f\end{aligned}\]

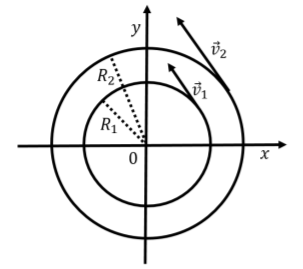
que a veces se llama la “frecuencia angular” en lugar de la velocidad angular. La velocidad angular realmente puede pensarse como una frecuencia, ya que representa la “cantidad de ángulo” por segundo que cubre un objeto cuando gira alrededor de un círculo. La velocidad angular no nos dice nada sobre la velocidad real del objeto, que depende del radio\(v=\omega R\). Esto se ilustra en la Figura\(\PageIndex{3}\), donde dos objetos pueden estar viajando alrededor de dos círculos de radio\(R_1\) y\(R_2\) con la misma velocidad angular\(\omega\). Si tienen la misma velocidad angular, entonces les tomará la misma cantidad de tiempo completar una revolución. Sin embargo, el objeto exterior tiene que cubrir una distancia mucho mayor (la circunferencia es mayor), y por lo tanto tiene que moverse con una velocidad lineal mayor.

Figura\(\PageIndex{3}\): Para una velocidad angular dada, la velocidad lineal será mayor en un círculo más grande\((v=\omega R)\).

Ejercicio\(\PageIndex{2}\)

Un motor está girando a\(3000\text{ rpm}\), ¿cuál es la frecuencia correspondiente en Hz?

1. \(5\text{ Hz}\)
2. \(50\text{ Hz}\)
3. \(500\text{ Hz}\)

Contestar

Pensamientos de Olivia

Hay un truco que me gusta usar para recordar cómo funcionan las velocidades lineales y angulares. La figura 4.4.4 muestra tu mano en dos posiciones, a las que llamamos (1) y (2).

Figura\(\PageIndex{4}\): Cómo usar la mano para entender mejor el movimiento circular.

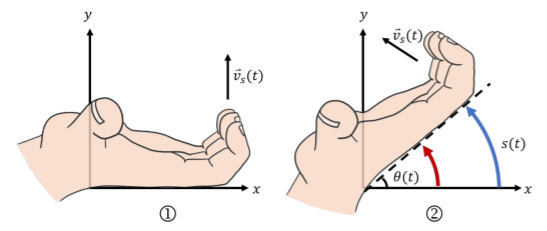
Digamos que quieres describir la ubicación de tus dedos en (2). Comienza poniendo tu mano en posición (1). Esta es la posición donde\(\theta=0\) y\(s=0\). Imagina que tu muñeca (o tu pulgar, lo que prefieras) se fija en el origen. Si mantienes tus dedos perpendiculares a tu mano, siempre señalarán en la\(s\) dirección positiva.

Imagina que tienes un manto azul de pintura en la parte posterior de tu meñique. Gira tu mano hasta que esté en posición (2). La longitud de la curva que hace la pintura es el valor de\(s\). El ángulo entre el dorso de tu mano y el\(x\) eje positivo es\(\theta\). Ahora, imagina que hay un manto rojo de pintura en tu palma. Toma la misma cantidad de tiempo para que tu palma llegue de la posición (1) a la posición (2) que para tus dedos. Dado que ambos atraviesan el mismo ángulo\(\theta\) en la misma cantidad de tiempo, la velocidad angular,\(\omega\) debe ser la misma para ambos. No obstante, la línea azul que dejan tus dedos será mucho más larga que la línea roja que deja tu palma. Tus dedos recorrieron una distancia mayor que tu palma en la misma cantidad de tiempo, por lo que deben tener una mayor velocidad lineal,\(v_s\). Cuanto más lejos estés de tu pulgar, mayor será la velocidad lineal, lo que sabemos por la fórmula\(v_s=R\omega\).

Si seguías girando tu mano alrededor del círculo, verías que tus dedos siempre apuntan en la misma dirección que tu velocidad lineal. Esto significa que si estás usando coordenadas cartesianas, la dirección de tu velocidad lineal siempre está cambiando.

Hay un par de limitaciones a este truco. Recuerda que esto solo funciona para el movimiento circular (el radio\(R\) debe ser constante) y que si te estás moviendo en la\(s\) dirección negativa, tus dedos apuntarán antiparalelo a la velocidad lineal.