8.4: Osciladores acoplados

Dos péndulos acoplados

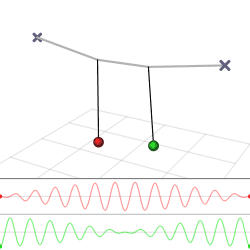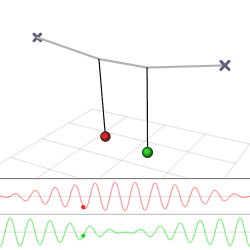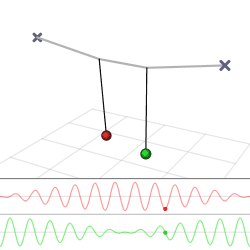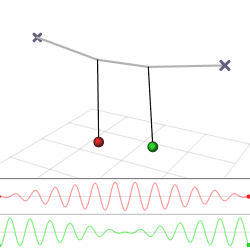
Una hermosa demostración de cómo la energía se puede transferir de un oscilador a otro es proporcionada por dos péndulos débilmente acoplados. Imagínese que tenemos dos péndulos idénticos de longitud\(L\) y masa\(m\), los cuales están conectados por un muelle débil con constante de resorte k (Figura\(\PageIndex{1a}\)).

Figura\(\PageIndex{1}\): Movimiento de dos péndulos acoplados. (a) Croquis de la configuración. Dos péndulos idénticos de longitud\(L\) y masa\(m\) están conectados a través de un resorte débil de constante de resorte\(k\). Como condición inicial, elegimos ambos péndulos en reposo, con el derecho en su posición de equilibrio y el izquierdo dado una amplitud finita. (b) Movimiento resultante de los dos péndulos: izquierdo (azul) y derecho (naranja).

La ecuación de movimiento del sistema combinado viene dada entonces por:

\[\begin{align} \dot{L} \ddot{\theta}_{1} &=-g \sin \theta_{1}-k L\left(\sin \theta_{1}-\sin \theta_{2}\right) \label{eqofmot1} \\ L \ddot{\theta}_{2} &=-g \sin \theta_{2}+k L\left(\sin \theta_{1}-\sin \theta_{2}\right) \label{eqofmot2} \end{align}\]

Una vez más utilizaremos la pequeña expansión angular en la que podemos aproximarnos\(\sin \theta \approx \theta\), e identificaremos\(\omega_0 = \sqrt{\frac{g}{L}}\) como la frecuencia de cada uno de los péndulos (desacoplados). Las ecuaciones\ ref {eqofmot1} y\ ref {eqofmot2} luego se convierten en

\[\begin{align} \ddot{\theta}_1 &=-\omega_{0}^{2} \theta_{1}-k \theta_{1}+k \theta_{2} \label{ddottheta1} \\[4pt] \ddot{\theta}_2 &=-\omega_{0}^{2} \theta_{2}+k \theta_{1}-k \theta_{2} \label{ddottheta2} \end{align}\]

Podemos resolver el sistema de ecuaciones diferenciales acopladas en Ecuaciones\ ref {ddottheta1} y\ ref {ddottheta2} fácilmente introduciendo dos nuevas variables:\(\alpha=\theta_{1}+\theta_{2}\) y\(\beta=\theta_{1}-\theta_{2}\), lo que nos da dos ecuaciones desacopladas:

\[\begin{align} \ddot{\alpha} &=-\omega_{0}^{2} \alpha \label{ddotalpha} \\[4pt] \ddot{\beta} &=-\omega_{0}^{2} \beta-2 k \beta=-\left(\omega^{\prime}\right)^{2} \beta \label{ddotbeta} \end{align}\]

donde\(\left(\omega^{\prime}\right)^{2}=\omega_{0}^{2}+2 k\) o\(\omega^{\prime}=\sqrt{2 k+g / L}\). Dado que las ecuaciones\ ref {ddotalpha} y\ ref {ddotbeta} son simplemente las ecuaciones de los osciladores armónicos, podemos anotar sus soluciones inmediatamente:

\[\begin{align} \alpha(t) &=A \cos \left(\omega_{0} t+\phi_{0}\right) \\ \beta(t) &=B \cos \left(\omega^{\prime} t+\phi^{\prime}\right) \end{align}\]

La conversión de nuevo a las variables originales\(\theta _1\) y también\(\theta _2\) es sencillo, y da

\[\begin{align}{\theta_{1}=\frac{1}{2}(\alpha+\beta)=\frac{A}{2} \cos \left(\omega_{0} t+\phi_{0}\right)+\frac{B}{2} \cos \left(\omega^{\prime} t+\phi^{\prime}\right)} \\ {\theta_{2}=\frac{1}{2}(\alpha-\beta)=\frac{A}{2} \cos \left(\omega_{0} t+\phi_{0}\right)-\frac{B}{2} \cos \left(\omega^{\prime} t+\phi^{\prime}\right)}\end{align}\]

Pongamos algunas condiciones iniciales específicas: dejamos el péndulo número 2 en reposo en su posición de equilibrio\((\theta_{2}(0)=\dot{\theta}_{2}(0)=0)\) y le damos al péndulo número 1 una amplitud finita pero también lo liberamos en reposo\((\theta_{1}(0)=\theta_{0}, \dot{\theta}_{1}(0)=0)\). Elaborar las cuatro incógnitas (\(A, B, \phi_0\)y\(\phi '\)) es sencillo, y obtenemos:

\[\begin{align}{\theta_{1}=\frac{\theta_{0}}{2} \cos \left(\omega_{0} t\right)+\frac{\theta_{0}}{2} \cos \left(\omega^{\prime} t\right)=\theta_{0} \cos \left(\frac{\omega_{0}+\omega^{\prime}}{2} t\right) \cos \left(\frac{\omega_{0}-\omega^{\prime}}{2} t\right)} \label{theta1} \\ {\theta_{2}=\frac{\theta_{0}}{2} \cos \left(\omega_{0} t\right)-\frac{\theta_{0}}{2} \cos \left(\omega^{\prime} t\right)=\theta_{0} \sin \left(\frac{\omega_{0}+\omega^{\prime}}{2} t\right) \sin \left(\frac{\omega^{\prime}-\omega_{0}}{2} t\right)} \label{theta2} \end{align}\]

La solución dada por las Ecuaciones\ ref {theta1} y\ ref {theta2} se grafica en la Figura\(\PageIndex{1}\). Tenga en cuenta que las soluciones tienen dos frecuencias (conocidas como las frecuencias propias del sistema). El rápido\(\frac{1}{2}\left(\omega_{0}+\omega^{\prime}\right)\), que para una constante de acoplamiento débil\(k\) está muy cerca de la frecuencia propia\(\omega_0\) de un solo péndulo, es la frecuencia a la que oscilan los péndulos. Lo hacen en antifase, como se expresa matemáticamente por el hecho de que una oscilación tiene un seno y la otra un coseno (que por supuesto es solo un seno desplazado\(\frac{\pi}{2}\)). La segunda frecuencia,\(\frac{1}{2}\left(\omega^{\prime}-\omega_{0}\right)\) es mucho más lenta, y representa la frecuencia a la que los dos péndulos transfieren energía entre sí, a través del resorte que los acopla. En la Figura\(\PageIndex{1b}\), es la frecuencia de la envolvente de la amplitud de la oscilación de cualquiera de los péndulos. Todos estos fenómenos volverán en la siguiente sección, en el estudio de las ondas, que viajan en un medio en el que muchos osciladores se acoplan entre sí (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Dos péndula colgando de una cuerda es un ejemplo de un par de osciladores acoplados. Observe el desplazamiento de amplitud de un péndulo a otro en el tiempo (Dominio Público; Lucas V. Barbosa vía Wikipedia)

Modos normales

Para un sistema con solo dos osciladores, la técnica que usamos anteriormente para resolver el sistema de Ecuaciones acopladas\ ref {eqofmot1} y\ ref {eqofmot2} es sencilla. Sin embargo, no se generaliza fácilmente a sistemas con muchos osciladores. En cambio, podemos explotar el hecho de que las ecuaciones son lineales y utilizar técnicas de álgebra lineal (como habrás adivinado del término frecuencia propia). Podemos reescribir las ecuaciones\ ref {eqofmot1} y\ ref {eqofmot2} en forma de matriz:

\[\frac{\mathrm{d}^{2}}{\mathrm{d} t^{2}}\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right)=\left(\begin{array}{cc}{-\left(\omega_{0}^{2}+k\right)} & {k} \\ {k} & {-\left(\omega_{0}^{2}+k\right)}\end{array}\right)\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right) \label{2oscmat}\]

La ecuación\ ref {2oscmat} es una ecuación diferencial homogénea de segundo orden con coeficientes constantes, muy parecida a la ecuación para un oscilador armónico simple y unidimensional. En consecuencia, podemos esperar que las soluciones también se vean similares, así que probamos nuestro Ansatz habitual:

\[\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right)=\left(\begin{array}{l}{C_{1}} \\ {C_{2}}\end{array}\right) e^{i \omega t} \label{ansatz}\]

donde\(C_1\) y\(C_2\) son constantes. Sustituyendo\ ref {ansatz} en\ ref {2oscmat} da

\[\left(\begin{array}{cc}{\omega_{0}^{2}+k} & {-k} \\ {-k} & {\omega_{0}^{2}+k}\end{array}\right)\left(\begin{array}{c}{C_{1}} \\ {C_{2}}\end{array}\right)=\omega^{2}\left(\begin{array}{c}{C_{1}} \\ {C_{2}}\end{array}\right) \label{subrslt}\]

que ojalá reconozcas como un problema de autovalor. Resolver para los valores propios\(\omega ^2\) da:

\[\left(-\omega^{2}+\omega_{0}^{2}+k\right)^{2}-k^{2}=0 \label{eigenval}\]

Como era de esperar, las soluciones de la Ecuación\ ref {eigenval} reproducen las frecuencias de las ecuaciones desacopladas en la Sección 8.4.1:

\[\omega_{+}^{2}=\omega_{0}^{2}, \quad \omega_{-}^{2}=\omega_{0}^{2}+2 k.\]

Los vectores propios de\ ref {subrslt} vienen dados por

\[\boldsymbol{C}_{+}=\frac{1}{\sqrt{2}}\left(\begin{array}{l}{1} \\ {1}\end{array}\right) \quad \text { for } \quad \omega_{+} \quad \text { and } \quad \mathbf{C}_{-}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{1} \\ {-1}\end{array}\right) \quad \text { for } \quad \omega_{-}\]

Obsérvese que los vectores propios son ortogonales; esta es una propiedad general de los vectores propios de las matrices simétricas. Cada vector propio corresponde a un posible estado estacionario de movimiento del sistema; estos estados se conocen como los modos normales ('normal' refiriéndose a la ortogonalidad de los vectores propios). Ahora podemos anotar inmediatamente la solución más general de la Ecuación\ ref {2oscmat} como una combinación lineal de los modos propios:

\[\left(\begin{array}{c}{\theta_{1}(t)} \\ {\theta_{2}(t)}\end{array}\right)=\frac{A_{+}}{2} e^{i\left(\omega_{+} t+\phi_{+}\right)}\left(\begin{array}{c}{1} \\ {1}\end{array}\right)+\frac{A_{-}}{2} e^{i\left(\omega_{-} t+\phi_{-}\right)}\left(\begin{array}{c}{1} \\ {-1}\end{array}\right)\]

donde las amplitudes\(A_{\pm}\) y fases\(\phi_{\pm}\) están determinadas por las condiciones iniciales.

Escribir nuestro sistema de ecuaciones en forma de matriz nos permite generalizar fácilmente tanto a configuraciones asimétricas (ver Problema 8.7) como a sistemas con muchos osciladores acoplados. Un ejemplo importante de este último caso es el estudio de las vibraciones en sólidos. Los átomos o iones en los sólidos suelen formar una red cristalina, que puede modelarse como un gran número de masas acopladas por resortes. Dichos cristales pueden tener propiedades vibracionales complicadas, que pueden ser analizadas en términos de sus modos normales. En particular, se puede acceder fácilmente a los modos con baja energía. Se les conoce como fonones, y corresponden a ondas sonoras en el sólido.