11.3: Algunas consecuencias de las transformaciones de Lorentz
- Page ID
- 129702
PÉRDIDA DE SIMULTANEIDAD
Si dos eventos son simultáneos para un observador en movimiento\(S^\prime\), el observador mide su intervalo de tiempo como\(\Delta t^\prime\). Si los dos eventos suceden en la misma posición (\(\Delta x^\prime = 0\)), las transformaciones de Lorentz dan\(\Delta x=0, \Delta t=0\) también. Sin embargo, si los dos eventos en\(S^\prime\) están espacialmente separados (\(\Delta x \neq 0\)), encontramos que para un observador en\(S\)\(\Delta t = \gamma (u)(u/c^2)\Delta x^\prime\), y por lo tanto los dos eventos no son simultáneos. Las cosas incluso empeoran: supongamos que dos eventos A y B ocurren a\(S\) una distancia de\(\Delta x\) distancia, y un intervalo de tiempo uno\(\Delta t\) después del otro. Ahora si\(\Delta x > (c/u)c\Delta t\), un observador en movimiento\(S^\prime\) concluirá eso\(\Delta t ^\prime <0\), lo que significa que el evento B ocurre antes del evento A! Afortunadamente, esto no viola la causalidad, ya que una señal de A a B (o viceversa) viajará como mucho con la velocidad de la luz, lo que, como veremos en la siguiente sección, significa que para las condiciones dadas, A y B no se pueden conectar causalmente, es decir, no se puede revertir causa y efecto, por muy rápido que tan rápido corres.
DILATACIÓN DEL TIEMPO Y CONTRACCIÓN DE LORENTZ
Un observador estacionario en cuadro\(S^\prime\) mide la diferencia de tiempo entre dos puntos para estar\(\Delta t^\prime\) en su propio reloj, mientras que un observador en\(S\) medirá la diferencia de tiempo en ese reloj (en movimiento) para ser\(\Delta t = \gamma (u)\Delta t^\prime\), exactamente el resultado de dilatación de tiempo que encontramos en la ecuación (10.2.1). De igual manera, un observador en\(S^\prime\) medirá la longitud de un palo estacionario a ser\(\Delta L^\prime\). Para un observador en\(S\), usando un método que llega a los extremos del palo simultáneamente (así\(\Delta t = 0\)), la longitud es\(\Delta L\). Tenemos\(\Delta x^\prime = \Delta L^\prime = \gamma(u)\Delta L\), entonces\(\Delta L=\Delta L^\prime/\gamma(u)\), que (como era de esperar) es el resultado de la contracción de Lorentz de la ecuación (10.2.5).
ADICIÓN DE VELOCIDAD
Calculamos la velocidad de un objeto\(v\)\(S\) medida en función de la velocidad\(v^\prime\) en\(S^\prime\) y la velocidad\(u\) de\(S^\prime\) en la ecuación (11.2.5). Sustituyendo los valores de las constantes que encontramos más adelante, obtenemos la siguiente ecuación:
\[v=\frac{u+v^{\prime}}{1+u v^{\prime} / c^{2}}\label{eq:1}\]
Por lo tanto, la ecuación (\(\ref{eq:1}\)) sigue directamente del postulado de luz, eso es todo lo que usamos para derivarlo. Demuestra matemáticamente que nunca se pueden agregar velocidades de tal manera que se supere la velocidad de la luz. \(u=v^\prime=c\)La configuración da\(v=c\), y para cualquier valor\(u<c\)\(v^\prime<c\),, siempre obtendrás\(v<c\).
Ecuación\ ref {eq:1} se mantiene para el movimiento en la misma dirección que el movimiento del marco de referencia, por ejemplo, si estás en un tren en movimiento, y rodando una bola a lo largo del tren. No obstante, también podrías hacer rodar la pelota en dirección transversal (digamos\(y\) si llamamos a la dirección en la que se mueve el tren\(x\)). Se podría pensar que la velocidad observada para el observador comoving y estacionario es la misma en ese caso (es para las transformaciones galileanas), pero ese no es el caso. Tenemos\(v_y = dy/dt\), y aunque\(dy\) es invariante, no\(dt\) lo es. Sin embargo, calcular\(v_y\) en términos de\(v_y^\prime\) (la velocidad a la que el observador en movimiento rueda la pelota) es sencillo, simplemente aplicamos la transformación de Lorentz a\(dt\):
\[v_{y}=\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{\mathrm{d} y^{\prime}}{\gamma(u) \mathrm{d}\left(t^{\prime}+\frac{u}{c^{2}} x^{\prime}\right)}=\frac{1}{\gamma(u)} \frac{\mathrm{d} y^{\prime} / \mathrm{d} t^{\prime}}{1+\frac{u}{c^{2}} \mathrm{d} x^{\prime} / \mathrm{d} t^{\prime}}=\frac{1}{\gamma(u)} \frac{v_{y}^{\prime}}{1+u v_{x}^{\prime} / c^{2}}\label{eq:2}\]
APLICACIÓN DE EJEMPLO: EFECTO RELATIVISTA DE FARO
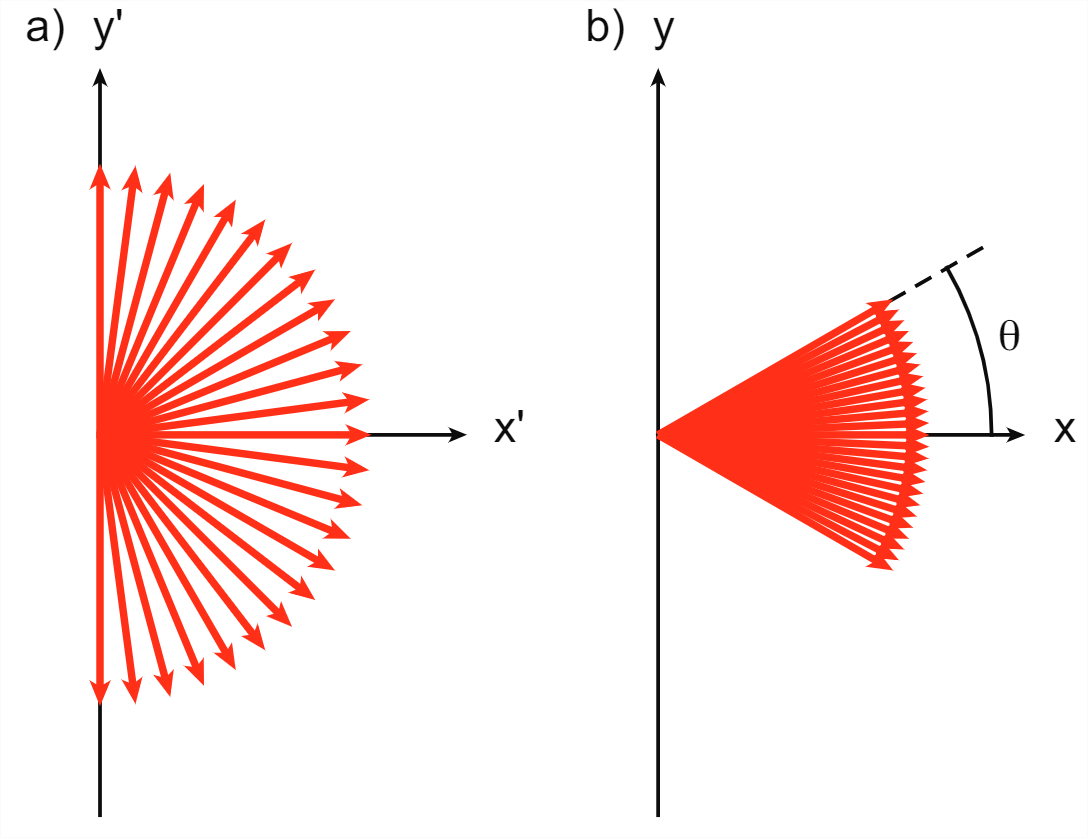
Supongamos que tiene una fuente de luz que irradia isotrópicamente (es decir, con la misma intensidad en todas las direcciones). ¿Qué pasa si ponemos la fuente de luz en un tren en movimiento? Sorprendentemente, según un observador estacionario, la fuente de luz ya no es isotrópica. Para entender lo que sucede, llamemos como de costumbre a la dirección en la que se mueve el tren\(x\) y su velocidad\(u\). Un rayo de luz emitido por la fuente de luz en\(S^\prime\) tiene una velocidad\(v^\prime\) con magnitud\(c\) (en la que ambos observadores coinciden), y componentes (\(v_x^\prime\),\(v_y^\prime\),\(v_z^\prime\)) (figura\(\PageIndex{1}\) a). Ahora consideremos el rayo de luz que se mueve a lo largo del\(y^\prime\) eje. Su velocidad viene dada por\(v^\prime = (0,c,0\)\). Podemos calcular los componentes de velocidad de este rayo de luz en cuadro\(S\) usando las Ecuaciones de transformación de velocidad\ ref {eq:1} y\ ref {eq:2}, que da\(v=(u,\gamma(u),0)\) (que por supuesto todavía tiene magnitud\(c\)). El rayo de luz capta así un componente en la\(x\) dirección positiva y, en consecuencia, obtiene un componente más pequeño en la\(y\) dirección. La Figura\(\PageIndex{1}\) b muestra el cono de luz resultante en la\(x\) dirección positiva. Su ángulo de apertura se\(\mu\) puede calcular fácilmente:
\[\sin (\theta)=\frac{v_{y}}{|v|}=\frac{v_{y}}{c}=\gamma(u)\]
Por razones que probablemente te resultarán fáciles de adivinar, a este fenómeno se le conoce como el efecto relativista de faros. Se observa en la radiación emitida por electrones que giran alrededor de líneas de campo magnético que orbitan Júpiter y el sol, así como en aceleradores de partículas en la tierra.