10.3: El principio de Hamilton

Ahora déjenme mostrar que las ecuaciones de movimiento de Lagrange, que se derivaron en la Sec. \(2.1\)de las leyes Newton, también pueden obtenerse del llamado principio Hamilton,\({ }^{16}\) es decir, la condición de un mínimo (o más bien un extremo) de la siguiente integral llamada acción:\[S \equiv \int_{t_{\text {ini }}}^{t_{\text {fin }}} L d t,\] dónde\(t_{\text {ini }}\) y\(t_{\text {fin }}\) son, respectivamente, los momentos inicial y final de tiempo, en el que todas las coordenadas y velocidades generalizadas se consideran fijas (no variadas) - ver Figura\(2 .\)

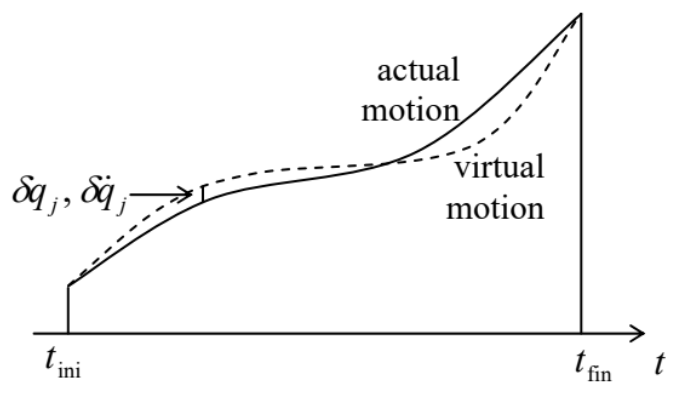Figura 10.2. Derivando el principio de Hamilton.

La prueba de esa afirmación (en el ámbito de la mecánica clásica) es bastante simple. Considerando, de manera similar a la Sec. 2.1, una posible variación virtual del movimiento, descrita por\(\left\{\delta q_{j}(t), \delta \dot{q}_{j}(t)\right\}\) desviaciones infinitesimales del movimiento real, la condición necesaria\(S\) para que sea mínimo es\[\delta S \equiv \int_{t_{\text {ini }}}^{t_{\text {fin }}} \delta L d t=0,\] dónde\(\delta S\) y\(\delta L\) son las variaciones de la acción y la Función Lagrange, correspondiente al conjunto\(\left\{\delta q_{j}(t), \delta \ddot{q}_{j}(t)\right\}\). Como ya se ha comentado en la Sec. 2.1, podemos utilizar la operación de variación igual que la diferenciación habitual (pero en un tiempo fijo, ver Figura 2), intercambiando estas dos operaciones si es necesario ver Figura\(2.3\) y su discusión. Así, podemos escribir\[\delta L=\sum_{j}\left(\frac{\partial L}{\partial q_{j}} \delta q_{j}+\frac{\partial L}{\partial \dot{q}_{j}} \delta \ddot{q}_{j}\right)=\sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j}+\sum_{j} \frac{\partial L}{\partial \dot{q}_{j}} \frac{d}{d t} \delta q_{j} .\] Después de enchufar la última expresión a la ecuación (48), podemos integrar el segundo término por partes:\[\begin{aligned} \delta S &=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t+\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \frac{\partial L}{\partial \dot{q}_{j}} \frac{d}{d t} \delta q_{j} d t \\ &=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t+\sum_{j}\left[\frac{\partial L}{\partial \dot{q}_{j}} \delta q_{j}\right]_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}}-\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \delta q_{j} d\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)=0 \end{aligned}\] Dado que las coordenadas generalizadas en los puntos inicial y final se consideran fijas (no afectadas por la variación), todas\(\delta q_{j}\left(t_{\mathrm{ini}}\right)\) y \(\delta q_{j}\left(t_{\mathrm{fin}}\right)\)desaparecer, de manera que el segundo término en la última forma de la Ec. (50) también se desvanece. Ahora multiplicando y dividiendo el último término de esa expresión por\(d t\), finalmente obtenemos\[\delta S=\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j} \frac{\partial L}{\partial q_{j}} \delta q_{j} d t-\sum_{j} \int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \delta q_{j} \frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right) d t=-\int_{t_{\mathrm{ini}}}^{t_{\mathrm{fin}}} \sum_{j}\left[\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial q_{j}}\right] \delta q_{j} d t=0\] Esta relación debe mantenerse para un conjunto arbitrario de funciones\(\delta q_{j}(t)\), y para cualquier intervalo de tiempo, y esto solo es posible si las expresiones entre corchetes son iguales a cero para todos \(j\), dándonos el conjunto de las ecuaciones de Lagrange (2.19). Entonces, el principio de Hamilton de hecho da las ecuaciones de movimiento de Lagrange.

Es fascinante ver cómo funciona el principio de Hamilton para casos particulares. Como ejemplo muy sencillo, consideremos el habitual oscilador lineal 1D, con la función Lagrangiana utilizada tantas veces antes en este curso:\[L=\frac{m}{2} \dot{q}^{2}-\frac{m \omega_{0}^{2}}{2} q^{2} .\] Como sabemos muy bien, las ecuaciones de movimiento de Lagrange para esto\(L\) están exactamente satisfechas por cualquier función sinusoidal con la frecuencia \(\omega_{0}\), en particular por una función simétrica del tiempo\[q_{\mathrm{e}}(t)=A \cos \omega_{0} t, \quad \text { so that } \dot{q}_{\mathrm{e}}(t)=-A \omega_{0} \sin \omega_{0} t .\] En un intervalo de tiempo limitado, digamos\(0 \leq \omega_{0} t \leq+\pi / 2\), esta función es bastante suave y puede ser bien aproximada por otras funciones de tiempo simples y razonablemente seleccionadas, por ejemplo,\[q_{\mathrm{a}}(t)=A\left(1-\lambda t^{2}\right), \quad \text { so that } \dot{q}_{\mathrm{a}}(t)=-2 A \lambda t,\] siempre que el parámetro \(\lambda\)también se selecciona de manera razonable. Tomemos\(\lambda=\left(\pi / 2 \omega_{0}\right)^{2}\), para que la función aproximada\(q_{\mathrm{a}}(t)\) coincida con la función exacta\(q_{\mathrm{e}}(t)\) en ambos extremos de nuestro intervalo de tiempo (Figura 3):\[q_{\mathrm{a}}\left(t_{\mathrm{ini}}\right)=q_{\mathrm{e}}\left(t_{\mathrm{ini}}\right)=A, \quad q_{\mathrm{a}}\left(t_{\mathrm{fin}}\right)=q_{\mathrm{e}}\left(t_{\mathrm{fin}}\right)=0, \quad \text { where } t_{\mathrm{ini}} \equiv 0, \quad t_{\mathrm{fin}} \equiv \frac{\pi}{2 \omega_{0}},\] y verificar cuál de ellas “prefiere” el principio de Hamilton, es decir, qué función da la menor acción.

Figura 10.3. Parcelas de las funciones\(q(t)\) dadas por las ecuaciones (53) y (54).

Un cálculo elemental de la acción (47), correspondiente a estas dos funciones, arroja\[S_{\mathrm{e}}=\left(\frac{\pi}{8}-\frac{\pi}{8}\right) m \omega_{0} A^{2}=0, \quad S_{\mathrm{a}}=\left(\frac{4}{3 \pi}-\frac{2 \pi}{15}\right) m \omega_{0} A^{2} \approx(0.4244-0.4189) m \omega_{0} A^{2}>0,\] con los primeros términos en todos los paréntesis provenientes de las integrales de tiempo de la energía cinética, y los segundos términos, de los de la energía potencial.

Este resultado muestra, primero, que la función exacta del tiempo, para la cual estas dos contribuciones cancelan exactamente,\({ }^{17}\) es efectivamente “preferible” para minimizar la acción. Segundo, para la función aproximada, las dos contribuciones a la acción son bastante cercanas a las exactas, y de ahí casi se cancelan entre sí, señalando que esta aproximación es muy razonable. Es evidente que en algunos casos cuando no se puede encontrar la solución analítica exacta de las ecuaciones de movimiento, la minimización de\(S\) mediante el ajuste de uno o más parámetros libres, incorporados a una función de “prueba” adivinada, puede ser utilizada para encontrar una aproximación razonable para la ley real del movimiento. 18It también es muy útil para hacer más transparente la noción de acción\(S\), definida por la Ec. (47), calculándola para el simple caso de que una sola partícula se mueva en un campo potencial que conserva su energía\(E=T+U\). En este caso, la función lagrangiana\(L=T-U\) puede ser representada como\[L=T-U=2 T-(T+U)=2 T-E=m v^{2}-E,\] con un tiempo independiente\(E\), de manera que\[S=\int L d t=\int m v^{2} d t-E t+\text { const. }\] Representando la expresión bajo la integral restante como\(m \mathbf{v} \cdot \mathbf{v} d t=\mathbf{p} \cdot(d \mathbf{r} / d t) d t=\mathbf{p} \cdot d \mathbf{r}\), finalmente obtenemos\[S=\int \mathbf{p} \cdot d \mathbf{r}-E t+\text { const }=S_{0}-E t+\text { const },\] donde el tiempo independiente integral\[S_{0} \equiv \int \mathbf{p} \cdot d \mathbf{r}\] se llama frecuentemente la acción abreviada.

Esta expresión puede ser utilizada para establecer una conexión más importante entre la mecánica clásica y la cuántica, ahora en su imagen de Schrödinger. En efecto, en la aproximación cuasiclásica (WKB) de esa imagen\({ }^{19}\) una partícula de energía fija es descrita por una onda de Broglie\[\Psi(\mathbf{r}, t) \propto \exp \left\{i\left(\int \mathbf{k} \cdot d \mathbf{r}-\omega t+\text { const }\right)\right\},\] donde el vector de onda\(\mathbf{k}\) es proporcional al momento de la partícula, y la frecuencia\(\omega\), a su energía:\[\mathbf{k}=\frac{\mathbf{p}}{\hbar}, \quad \omega=\frac{E}{\hbar} .\] Al enchufar estas expresiones en la ecuación (61) y comparar el resultado con la ecuación (59), vemos que la función de onda WKB puede representarse como\[\Psi \propto \exp \{i S / \hbar\} .\] De ahí que el principio de Hamilton (48) significa que la fase total de la función de onda cuasiclásica debe ser mínima a lo largo de la trayectoria real de la partícula. Pero este es exactamente el llamado principio mínimo eikonal bien conocido desde la óptica (aunque válido también para cualquier otra onda), donde sirve para definir las trayectorias de los rayos en el límite de la óptica geométrica, similar a la condición de aproximación WKB. Así, la relación\(S / \hbar\) puede considerarse igual que el eikonal, es decir, la acumulación de fase total, de las ondas de Broglie. \({ }^{20}\)

Ahora, comparando la ecuación (60) con la ecuación (39), vemos que la variable de acción\(J\) es solo el cambio de la acción abreviada\(S_{0}\) a lo largo de un solo contorno de plano de fase (dividido por\(2 \pi\)). Esto significa, en particular, que en la aproximación WKB,\(J\) está el número de ondas de Broglie a lo largo de la trayectoria clásica de una partícula, es decir, un valor entero del número cuántico correspondiente. Si los parámetros del sistema se cambian lentamente, el número cuántico tiene que permanecer entero, y por lo tanto\(J\) no puede cambiar, dando una interpretación cuántica mecánica de la invarianza adiabática. Esto es realmente fascinante: un hecho de la mecánica clásica puede ser “derivado” (o al menos entendido) más fácilmente desde el punto de vista de la mecánica cuántica. \({ }^{21}\)

---

\({ }^{16}\)También se le llama el “principio de menor acción”, o el “principio de acción estacionaria”. (Estos nombres pueden ser más justos en el contexto de una larga historia del desarrollo del principio, partiendo de sus formas particulares más simples, que incluye los nombres de P. de Fermat, P. Maupertuis, L. Euler, y J.-L. Lagrange.)

\({ }^{17}\)Dicha cancelación, es decir, la igualdad\(S=0\), por supuesto no es el requisito general; es específica sólo para este ejemplo en particular.

\({ }^{18}\)Esto es esencialmente un análogo clásico del método variacional de la mecánica cuántica - véase, por ejemplo, QM Sec. \(2.9 .\)

\({ }^{19}\)Véase, por ejemplo, QM Sec. 3.1.

\({ }^{20}\)En efecto, la Ec. (63) fue el punto de partida para el desarrollo de R. Feynman de su formulación integral de la mecánica cuántica -véase, por ejemplo, QM Sec. 5.3.

\({ }^{21}\)Como recordatorio, nos hemos topado con una sorpresa igualmente agradable en nuestra discusión sobre la excitación paramétrica no degenerada en la Sec. \(6.7\).

\({ }^{22}\)Véase, por ejemplo, los capítulos 6-9 en I. C. Percival y D. Richards, Introducción a la dinámica, Cambridge U. Press,\(1983 .\)