4.5: Péndulo plano de accionamiento armónico, amortiguado linealmente

El péndulo plano armónicamente amortiguado linealmente ilustra muchos de los fenómenos exhibidos por los sistemas no lineales a medida que evolucionan de un movimiento ordenado a un movimiento caótico. Ilustra el hecho notable de que el determinismo no implica ni un comportamiento regular ni previsibilidad. El conocido péndulo amortiguado linealmente accionado armónicamente proporciona una base ideal para una introducción a la dinámica no lineal ¹.

Considere un péndulo plano amortiguado linealmente accionado armónicamente de momento de inercia\(I\) y masa\(m\) en un campo gravitacional que es impulsado por un par debido a una fuerza que\(F(t)=F_{D}\cos \omega t\) actúa en un brazo de momento\(L\). El término de amortiguación es\(b\) y el desplazamiento angular del péndulo, relativo a la vertical, es\(\theta\). La ecuación de movimiento del péndulo simple amortiguado linealmente accionado armónico-se puede escribir como

\[I \ddot{\theta}+b\dot{\theta}+mgL\sin \theta =LF_{D}\cos \omega t \label{4.28}\]

Tenga en cuenta que la fuerza de restauración sinusoidal para el péndulo plano no es lineal para ángulos grandes\(\theta\). El periodo natural del péndulo libre es

\[\omega _{0}=\sqrt{\frac{mgL}{I}}\]

Un parámetro adimensional\(\gamma\), que se llama fuerza motriz, se define por\[\gamma \equiv \frac{F_{D}}{mg}\]

La ecuación de movimiento\ ref {4.28} puede generalizarse introduciendo unidades adimensionales tanto para el tiempo\(\tilde{t}\) como para la frecuencia de accionamiento relativa\( \tilde{\omega}\) definidas por

\[\tilde{t}\equiv \omega _{0}t\hspace{1in}\tilde{\omega}\equiv \frac{\omega }{ \omega _{0}}\]

Además, defina el factor de amortiguación inversa\(Q\) como

\[Q\equiv \frac{\omega _{0}I}{b}\]

Estas definiciones permiten que la ecuación\ ref {4.28} se escriba en forma adimensional\[\frac{d^{2}\theta }{d\tilde{t}^{2}}+\frac{1}{Q}\frac{d\theta }{d\tilde{t}} +\sin \theta =\gamma \cos \tilde{\omega}\tilde{t} \label{4.33}\]

El comportamiento del ángulo\(\theta\) para el péndulo plano amortiguado impulsado depende de la fuerza de accionamiento\(\gamma\) y del factor de amortiguación\(Q\). Consideremos el caso donde se evalúa la Ecuación\ ref {4.33} asumiendo que el coeficiente de amortiguación\(Q=2\), y que la frecuencia angular relativa\(\tilde{\omega}= \frac{2}{3},\) que está cerca de la resonancia donde se manifiestan fenómenos caóticos. Se utiliza el método Runge-Kutta para resolver esta ecuación no lineal de movimiento.

Cerca de Linealidad

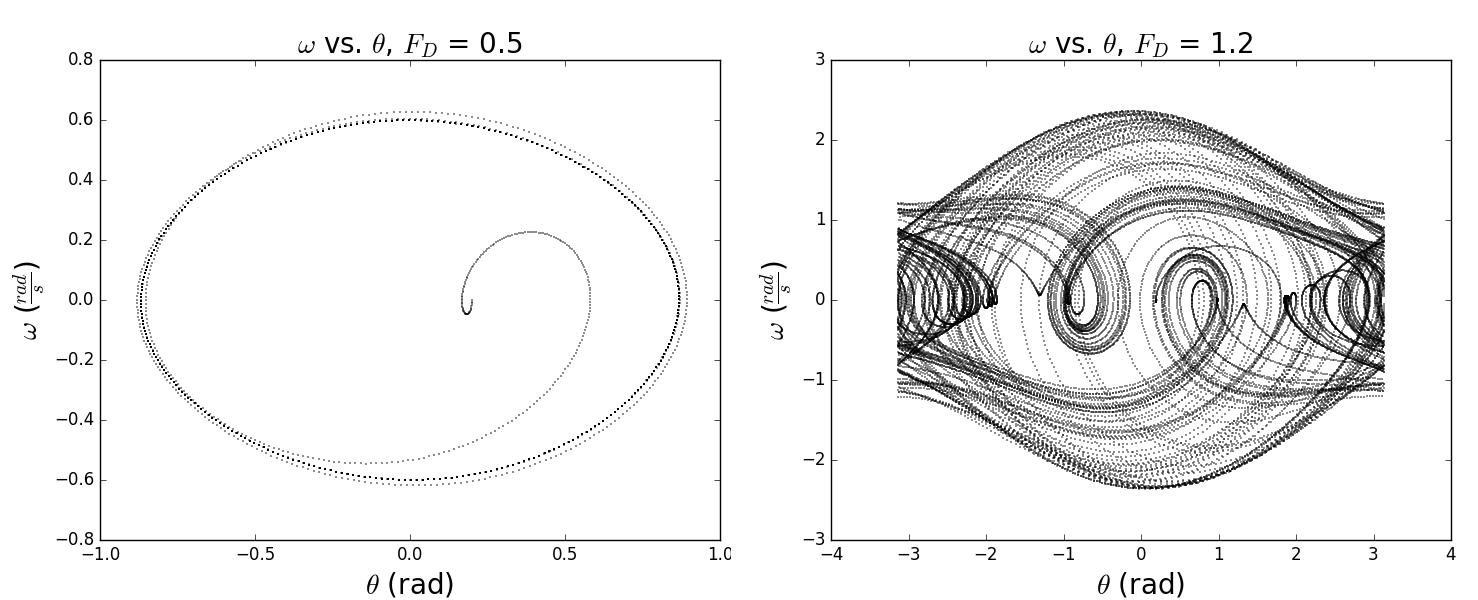
Para\(\gamma =0.2\) la fuerza de accionamiento, la amplitud es lo suficientemente pequeña como para que se aplique la\( \sin \theta \simeq \theta ,\) superposición, y la solución es idéntica a la del oscilador lineal amortiguado linealmente accionado. Como se muestra en la Figura\(\PageIndex{1}\), una vez que la solución transitoria muere, la solución de estado estacionario se acerca asintóticamente a un atractor que tiene una amplitud de\( \pm 0.3\) radianes y un desplazamiento de fase\(\delta\) con respecto a la fuerza impulsora. La abscisa se da en unidades del tiempo adimensional\(\tilde{t} =\omega _{0}t\). La solución transitoria depende de las condiciones iniciales y muere después de aproximadamente\(5\) períodos, mientras que la solución de estado estacionario es independiente de las condiciones iniciales y tiene un diagrama estado-espacio que tiene una forma elíptica, característica del oscilador armónico. Para todas las condiciones iniciales, el diagrama de dependencia del tiempo y espacio de estado para el movimiento en estado estacionario se aproxima a una solución única, llamada "atractor “, es decir, el péndulo oscila sinusoidalmente con una amplitud dada a la frecuencia de la fuerza impulsora y con un desplazamiento de fase constante\(\delta\), i.e.

\[\theta (t)=A\cos (\omega t-\delta ).\]

Esta solución es idéntica a la del oscilador lineal de accionamiento armónico, amortiguado linealmente discutido en el capítulo\(3.6.\)

Figura\(\PageIndex{1}\): Movimiento del péndulo amortiguado accionado para las resistencias de accionamiento de\(\gamma = 0.2\)\(\gamma = 0.9\),\(\gamma = 1.05\), y\(\gamma = 1.078\). El lado izquierdo muestra la dependencia del tiempo del ángulo de deflexión\(\theta\) con el eje de tiempo expresado en unidades adimensionales\(\tilde t\). En el lado derecho se muestran las correspondientes parcelas estado-espacio. Estas parcelas asumen\(\tilde \omega = \frac{\omega}{\omega_0} = \frac{2}{3}\)\(Q = 2\),, y el movimiento comienza con\(\theta = \omega = 0\).

Figura\(\PageIndex{2}\): El péndulo amortiguado impulsado asumiendo que\(\tilde \omega = \frac{2}{3}\)\(Q = 2\), con condiciones iniciales\(\theta (0) = −\frac{\pi}{2}\),\(\omega (0) = 0\). El sistema exhibe movimiento del período dos para las intensidades de accionamiento\(\gamma = 1.078\) como se muestra en el diagrama de espacio de estado para ciclos\(10 − 20\). Para\(\gamma = 1.081\) el sistema se muestra movimiento del período cuatro para ciclos\(10 − 30\).

Débil no linealidad

La figura\(\PageIndex{1}\) muestra que para la fuerza de accionamiento\(\gamma =0.9\), después de que la solución transitoria muere, la solución de estado estacionario se asienta en un atractor que oscila a la frecuencia de accionamiento con una amplitud de un poco más de\(\frac{\pi }{2}\) radianes para los que falla la aproximación de ángulo pequeño. La distorsión debida a la no linealidad es exhibida por la forma no elíptica del diagrama estado-espacio.

El comportamiento observado se puede calcular utilizando el método de aproximación sucesiva discutido en el capítulo\(4.2\). Es decir, cerca de ángulos pequeños, la función sinusoidal se puede aproximar reemplazando

\[\sin \theta \approx \theta -\frac{1}{6}\theta ^{3}\]

en Ecuación\ ref {4.33} para dar

\[\ddot{\theta}+\frac{1}{Q}\dot{\theta}+\omega _{0}^{2}\left( \theta -\frac{1}{ 6}\theta ^{3}\right) =\gamma \cos \tilde{\omega}\tilde{t} \label{4.35}\]

Como primera aproximación supongamos que

\[\theta (\tilde{t})\approx A\cos (\tilde{\omega}\tilde{t}-\delta )\]

entonces el\(\theta^{3}\) término pequeño en la Ecuación\ ref {4.35} aporta un término proporcional a\(\cos ^{3}(\tilde{\omega}\tilde{t}-\delta )\). Pero

\[\cos ^{3}(\tilde{\omega}\tilde{t}-\delta )=\frac{1}{4}\left( \cos 3(\tilde{ \omega}\tilde{t}-\delta )+3\cos (\tilde{\omega}\tilde{t}-\delta )\right)\]

Es decir, la no linealidad introduce un pequeño término proporcional a\(\cos 3(\omega t-\delta )\). Dado que el lado derecho de la Ecuación\ ref {4.35} es una función de sólo\(\cos \omega t,\) entonces los términos en\(\theta ,\dot{\theta},\) y\(\ddot{\theta}\) en el lado izquierdo deben contener el tercer\( \cos 3(\omega t-\delta )\) término armónico. Así una mejor aproximación a la solución es de la forma

\[\theta (\tilde{t})=A\left[ \cos (\tilde{\omega}\tilde{t}-\delta )+\varepsilon \cos 3(\tilde{\omega}\tilde{t}-\delta )\right]\]

donde el coeficiente de mezcla\(\varepsilon <1\). Este método de aproximación sucesiva se puede repetir para agregar términos adicionales proporcionales a\(\cos n(\omega t-\delta )\) donde\(n\) es un entero con\(n\geq 3\). Así, la no linealidad introduce armónicos\(n\) progresivamente más débiles en la solución. Este enfoque de aproximación sucesiva es viable solo cuando el coeficiente de mezcla\(\varepsilon <1.\) Tenga en cuenta que estos armónicos son múltiplos enteros de\(\omega\), por lo tanto, la respuesta de estado estacionario es idéntica para cada período completo a pesar de que los contornos del espacio de estado se desvían de una forma elíptica.

Inicio de la complicación

La figura\(\PageIndex{1}\) muestra que para\(\gamma =1.05\) la fuerza de accionamiento es lo suficientemente fuerte como para hacer que la solución transitoria para el péndulo gire a través de dos ciclos completos antes de asentarse en una única solución de atractor de estado estacionario a la frecuencia de accionamiento. Sin embargo, esta solución atrayente se desplaza dos rotaciones completas con respecto a la condición inicial. El diagrama de espacio de estado muestra claramente el movimiento de balanceo de la solución transitoria durante los dos primeros períodos previos a que el sistema se asiente en un solo atractor de estado estacionario. El enfoque de aproximación sucesiva falla completamente a esta fuerza de acoplamiento ya que\(\theta\) oscila a través de grandes valores que son múltiplos de\(\pi .\)

La figura\(\PageIndex{1}\) muestra que para\(\gamma =1.078\) la fuerza motriz el movimiento evoluciona a un movimiento periódico mucho más complicado con un periodo que es tres veces el periodo de la fuerza motriz. Además, la amplitud excede\( 2\pi\) correspondiente al péndulo oscilando sobre el punto muerto superior con el centroide del movimiento desplazado por\(3\pi\) la condición inicial. Tanto el diagrama estado-espacio, como la dependencia temporal del movimiento, ilustran la complejidad de este movimiento que depende sensiblemente de la magnitud de la fuerza motriz\(\gamma ,\) además de las condiciones iniciales,\((\theta (0),\omega (0))\) y del factor de amortiguación\(Q\) como se muestra en la Figura\(\PageIndex{2}\)

Duplicación de periodos y bifurcación

Para la fuerza de accionamiento\(\gamma =1.078,\) con la condición inicial,\(\left( \theta (0),\omega \left( 0\right) \right) =\left( 0,0\right) ,\) el sistema exhibe un movimiento regular con un período que es tres veces el período de accionamiento. Por el contrario, si la condición inicial es\([\theta (0)=-\frac{\pi }{2} ,\omega \left( 0\right) =0]\) entonces, como se muestra en la Figura\(\PageIndex{2}\), la solución de estado estacionario tiene la frecuencia de accionamiento sin desplazamiento en\(\theta\), es decir, exhibe oscilación del período uno. Esta aparición de dos atractores separados y muy diferentes para\(\gamma =1.078,\) usar diferentes condiciones iniciales, se llama bifurcación.

Una característica adicional de la respuesta del sistema para\(\gamma =1.078\) es que cambiar las condiciones iniciales para\([\theta (0)=-\frac{\pi }{2},\omega \left( 0\right) =0]\) mostrar que la amplitud de los períodos pares e impares de oscilación difieren ligeramente en forma y amplitud, es decir, el sistema realmente tiene oscilación de período dos. Este movimiento del período dos, es decir, la duplicación del período, está claramente ilustrado por el diagrama de espacio de estados en que, aunque el movimiento todavía está dominado por oscilaciones del período uno, los ciclos par e impar se desplazan ligeramente. Así, para diferentes condiciones iniciales, el sistema para\(\gamma =1.078\) bifurca en cualquiera de dos atractores que tienen formas de onda muy diferentes, una de las cuales exhibe duplicación de período.

La duplicación de periodo exhibida para\(\gamma =1.078,\) es seguida por una segunda duplicación de periodo cuando\(\gamma =1.081\) como se muestra en la Figura\(\PageIndex{2}\). Con el incremento en la fuerza motriz esta duplicación de periodo sigue aumentando en múltiplos binarios a periodo\(8\)\(16\)\(32\),,,\(64\) etc. Numéricamente se encuentra que el umbral para la duplicación\(\gamma _{1}=1.0663,\) del periodo es de dos a cuatro ocurre en\(\gamma _{2}=1.0793\) etc. Feigenbaum demostró que esta cascada aumenta con el incremento en la fuerza motriz de acuerdo a la relación que obedece

\[(\gamma _{n+1}-\gamma _{n})\simeq \frac{1}{\delta }(\gamma _{n}-\gamma _{n-1})\]

donde\(\delta =4.6692016\),\(\delta\) se llama un número Feigenbaum. Como\( n\rightarrow \infty \ \) esta secuencia en cascada va a un límite\(\gamma _{c}\) donde\[\gamma _{c}=1.0829\]

Movimiento rodante

Se demostró que para\(\gamma >1.05\) la solución transitoria provoca que el péndulo tenga desviaciones angulares superiores\(2\pi\), es decir, el sistema rueda sobre el punto muerto superior. Para las resistencias de accionamiento en el rango,\(1.3<\gamma <1.4,\) la solución de estado estacionario para el sistema experimenta un movimiento de balanceo continuo como se ilustra en la Figura\(\PageIndex{3}\). La dependencia del tiempo para el ángulo exhibe un movimiento oscilatorio periódico superpuesto sobre un movimiento rodante monótono, mientras que la dependencia del tiempo de la frecuencia angular\(\omega =\frac{ d\theta }{dt}\) es periódica. Las gráficas de espacio de estado para movimiento rodante corresponden a una cadena de bucles con un espaciado de\(2\pi\) entre cada bucle. El diagrama de espacio de estado para el movimiento rodante se presenta de manera más compacta si el origen se desplaza\(2\pi\) por revolución para mantener la gráfica dentro de los límites como se ilustra en la Figura\(\PageIndex{3c}\).

Figura\(\PageIndex{3}\): Movimiento rodante para el péndulo plano amortiguado accionado para\(\gamma = 1.4\). (a) La dependencia del tiempo del ángulo\(\theta (t)\) aumenta\(2\pi\) por período de impulsión mientras que (b) la velocidad angular\(\omega (t)\) exhibe periodicidad. (c) La gráfica de espacio estatal para movimiento rodante se muestra con el origen desplazado\(2\pi\) por revolución para mantener la trama dentro de los límites\(−\pi < \theta < +\pi\)

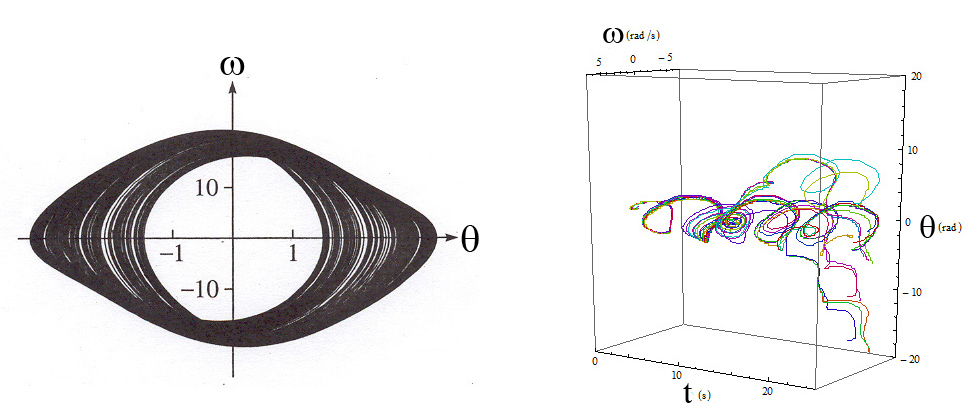
Inicio del caos

Cuando la fuerza de accionamiento se incrementa para\(\gamma =1.105,\) entonces el sistema no se acerca a un atractor único como se ilustra en la Figura\(\PageIndex{4 left}\) que muestra órbitas de espacio de estado para ciclos\(25-200\). Obsérvese que estas órbitas no se repiten implicando el inicio del caos. Para las resistencias de accionamiento mayores que\( \gamma _{c}=1.0829\) el plano amortiguado impulsado, el péndulo comienza a exhibir un comportamiento caótico. El inicio del movimiento caótico se ilustra haciendo una gráfica\(3\) -dimensional que combina la coordenada temporal con las coordenadas estado-espacio como se ilustra en la Figura\(\PageIndex{4 right}\). Esta gráfica muestra\(16\) trayectorias que comienzan en diferentes valores iniciales en el rango\(-0.15<\theta <0.15\) para\(\gamma =1.168\). Algunas soluciones son erráticas ya que, al intentar oscilar a la frecuencia de accionamiento, nunca se asientan en un movimiento periódico constante que es característico del movimiento caótico. La figura\(\PageIndex{4 right}\) ilustra la considerable sensibilidad del movimiento a las condiciones iniciales. Es decir, este sistema determinista puede exhibir ya sea orden, o caos, dependiendo de minúsculas diferencias en las condiciones iniciales.

Figura\(\PageIndex{4}\): Izquierda: Órbitas espacio-espacio para el péndulo amortiguado impulsado con\(\gamma = 1.105\). Tenga en cuenta que las órbitas no se repiten para los ciclos 25 a 200. Derecha: Diagrama tiempo-estado-espacio para\(\gamma = 1.168\). La gráfica muestra 16 trayectorias comenzando con diferentes valores iniciales en el rango\(−0.15 < \theta < 0.15\).

Figura\(\PageIndex{5}\): Gráficas estado-espacio para el péndulo accionado armónicamente, linealmente amortiguado, para amplitudes de conducción de\(F_D = 0.5\) y\(F_D = 1.2\). Estos cálculos se realizaron utilizando el método Runge-Kutta por E. Shah, (Comunicación privada)

---

¹ Un enfoque similar es utilizado por el libro “Chaotic Dynamics” de Baker y Gollub [Bak96].