4.6: Diferenciación entre movimiento ordenado y caótico

El capítulo\(4.5\) mostró que el movimiento en sistemas no lineales puede exhibir tanto orden como caos. La transición entre el movimiento ordenado y el movimiento caótico depende sensiblemente tanto de las condiciones iniciales como de los parámetros del modelo. Es sorprendentemente difícil distinguir sin ambigüedades entre movimiento ordenado complicado y movimiento caótico. Además, el movimiento puede fluctuar entre el orden y el caos de manera errática dependiendo de las condiciones iniciales. La extrema sensibilidad a las condiciones iniciales del movimiento para sistemas no lineales, hace esencial contar con medidas cuantitativas que puedan caracterizar el grado de orden, e interpretar el complicado movimiento dinámico de los sistemas. Como ilustración, considere el péndulo accionado armónicamente, linealmente amortiguado, con\(Q = 2,\) y fuerza motriz\(F(t) = F_{D}\sin \tilde{\omega}\tilde{t}\) donde\(\tilde{\omega} = \frac{2}{3}\). La figura (4.5.5) muestra las gráficas estado-espacio para dos amplitudes de conducción,\( F_{D} = 0.5\) lo que conduce a un movimiento ordenado y\(F_{D} = 1.2\) que conduce a un posible movimiento caótico. Se puede observar que para\(F_{D} = 0.5\) el diagrama estado-espacio converge en un solo atractor una vez que la solución transitoria ha muerto. Esto contrasta con el caso de\(F_{D} = 1.2,\) donde el diagrama estado-espacio no converge a un solo atractor, sino que exhibe un posible movimiento caótico. Se pueden utilizar tres medidas cuantitativas para diferenciar el movimiento ordenado del movimiento caótico para este sistema; a saber, el exponente Lyapunov, el diagrama de bifurcación y la sección de Poincaré, como se ilustra a continuación.

Exponente Lyapunov

El exponente de Lyapunov proporciona una medida cuantitativa y útil de la inestabilidad de las trayectorias, y la rapidez con que divergen las condiciones iniciales cercanas. Compara dos sistemas idénticos que comienzan con una diferencia infinitesimalmente pequeña en las condiciones iniciales para determinar si convergen al mismo atractor en tiempos largos, correspondientes a un sistema estable, o si divergen a atractores muy diferentes, característicos del movimiento caótico. Si la separación inicial entre las trayectorias en el espacio de fase at\(t = 0\) es\(\left\vert \delta Z_{0}\right\vert\), entonces para primer orden se puede suponer que la dependencia temporal de la diferencia depende exponencialmente del tiempo. Es decir,

\[\left\vert \delta Z(t)\right\vert \sim e^{\lambda t}\left\vert Z_{0}\right\vert\]

donde\(\lambda\) está el exponente Lyapunov. Es decir, el exponente de Lyapunov se define como\[\lambda = \lim_{t\rightarrow \infty }\lim_{\delta Z_{0}\rightarrow 0}\frac{1}{ t}\ln \frac{\left\vert \delta Z(t)\right\vert }{\left\vert Z_{0}\right\vert }\]

Sistemas para los que el exponente Lyapunov\(\lambda <0\) (negativo), converge exponencialmente a la misma solución atrayente en largos tiempos desde\(\left\vert \delta Z(t)\right\vert \rightarrow 0\) para\(t\rightarrow \infty\). Por el contrario, los sistemas para los cuales\(\lambda >0\) (positivo) divergen a soluciones completamente diferentes a largo plazo, es decir,\(\left\vert \delta Z(t)\right\vert \rightarrow \infty\) para\(t\rightarrow \infty\). Incluso para diferencias infinitesimalmente pequeñas en las condiciones iniciales, los sistemas que tienen un exponente Lyapunov positivo divergen a diferentes atractores, mientras que cuando el exponente\(\lambda <0\) Lyapunov corresponden a soluciones estables.

Figura\(\PageIndex{1}\): Gráficas de Lyapunov\(\Delta \theta\) versus tiempo para dos puntos de partida iniciales que difieren en\(\Delta \theta_0 = 0.001\)\(rads\). Los parámetros son\(Q = 2\), y\(F(t) = F_D \sin( \frac{2}{3}t)\), y\(\Delta t = 0.04\)\(s\). El exponente de Lyapunov para el\(F_D = 0.5\) que se dibuja como una línea discontinua, es convergente con\(\lambda = −0.251\). Para\(F_D = 1.2\) el exponente es divergente como lo indica la línea discontinua que como pendiente de\(\lambda = 0.1538\). Estos cálculos se realizaron utilizando el método Runge-Kutta por E. Shah, (Comunicación privada)

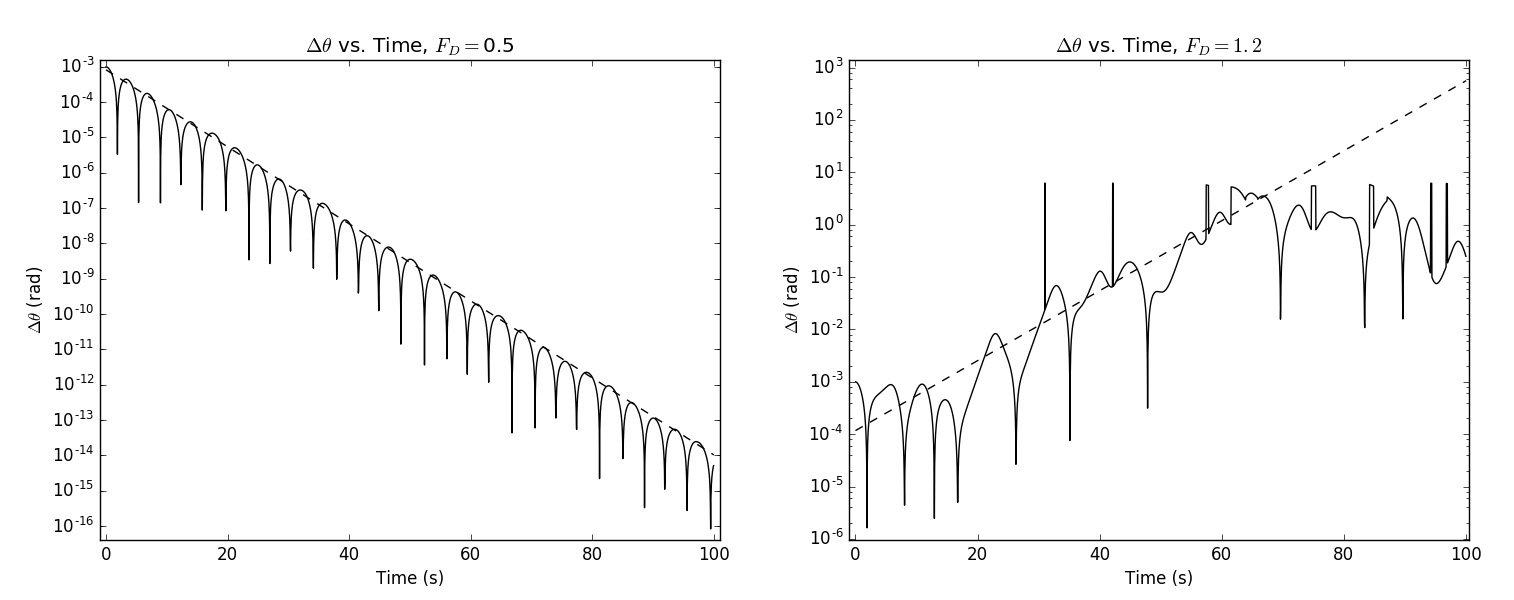
La figura\(\PageIndex{1}\) ilustra gráficas de Lyapunov para el péndulo plano de accionamiento armónico, linealmente amortiguado, con las mismas condiciones discutidas en el capítulo\(4.5\). Tenga en cuenta que para la pequeña amplitud de conducción\(F_{D} = 0.5,\) la gráfica de Lyapunov converge al movimiento ordenado con un exponente\(\lambda = -0.251,\) mientras que para\(F_{D} = 1.2,\) la gráfica diverge característica del movimiento caótico con un exponente\(\lambda = 0.1538.\) El exponente de Lyapunov generalmente fluctúa ampliamente a la frecuencia del oscilador local , y así el promedio de tiempo del exponente Lyapunov debe tomarse durante muchos periodos de la oscilación para identificar la tendencia general con el tiempo. Algunos sistemas cercanos a una transición de orden a caos pueden exhibir exponentes positivos de Lyapunov por tiempos cortos, característicos del caos, y luego converger a negativo\(\lambda\) en un tiempo más largo, lo que implica movimiento ordenado. Los exponentes de Lyapunov se utilizan ampliamente para monitorear la estabilidad de las soluciones para sistemas no lineales. Por ejemplo, el exponente Lyapunov se utiliza para identificar si el flujo de fluido es laminar o turbulento como se discute en el capítulo\(16.8\).

Un sistema dinámico en espacio de fases\(n\) -dimensional contará con un conjunto de exponentes\(n\) Lyapunov\(\{\lambda _{1},\lambda _{2},\dots ,\lambda _{n}\}\) asociados a un conjunto de atractores, cuya importancia depende de las condiciones iniciales. Por lo general, un exponente de Lyapunov domina en una ubicación específica en el espacio de fases, y por lo tanto es habitual utilizar el exponente máximo de Lyapunov para identificar el caos. El exponente Lyapunov es una medida muy sensible del inicio del caos y proporciona una prueba importante de la naturaleza caótica para el movimiento complicado que exhiben los sistemas no lineales.

Diagrama de bifurcación

El diagrama de bifurcación simplifica la presentación del movimiento dinámico al muestrear el estado del sistema una vez por periodo, sincronizado con la frecuencia de conducción, para muchos conjuntos de condiciones iniciales. Los resultados se presentan gráficamente en función de un parámetro del sistema en el diagrama de bifurcación. Por ejemplo, el comportamiento tremendamente diferente en el péndulo del plano amortiguado accionado se representa en un diagrama de bifurcación en la Figura\(\PageIndex{2}\), que muestra la velocidad angular observada\(\omega\) del péndulo muestreado una vez por ciclo de conducción trazado frente a la fuerza de accionamiento. El diagrama de bifurcación se obtiene muestreando ya sea el ángulo\(\theta\), o la velocidad angular\(\omega\), una vez por ciclo de conducción, es decir, representa los observables del péndulo mediante una técnica estroboscópica que muestrea el movimiento sincrónico con la frecuencia de accionamiento. Las gráficas de bifurcación también se pueden crear en función del tiempo\( \tilde{t}\), del factor de amortiguación\(Q\), de la frecuencia\(\tilde{\omega} = \frac{\omega }{\omega _{0}}\) normalizada o de la amplitud de conducción\(\gamma\).

Figura\(\PageIndex{2}\): El diagrama de bifurcación muestrea la velocidad angular\(\omega\) una vez por periodo para el péndulo plano accionado, linealmente amortiguado, trazado en función de la fuerza de accionamiento\(\gamma\). Las regiones de duplicación de época y el caos, así como las islas de estabilidad, se manifiestan a medida que\(\gamma\) se cambia la fuerza motriz. Tenga en cuenta que el número limitado de muestras provoca el ensanchamiento de las líneas adyacentes a las bifurcaciones.

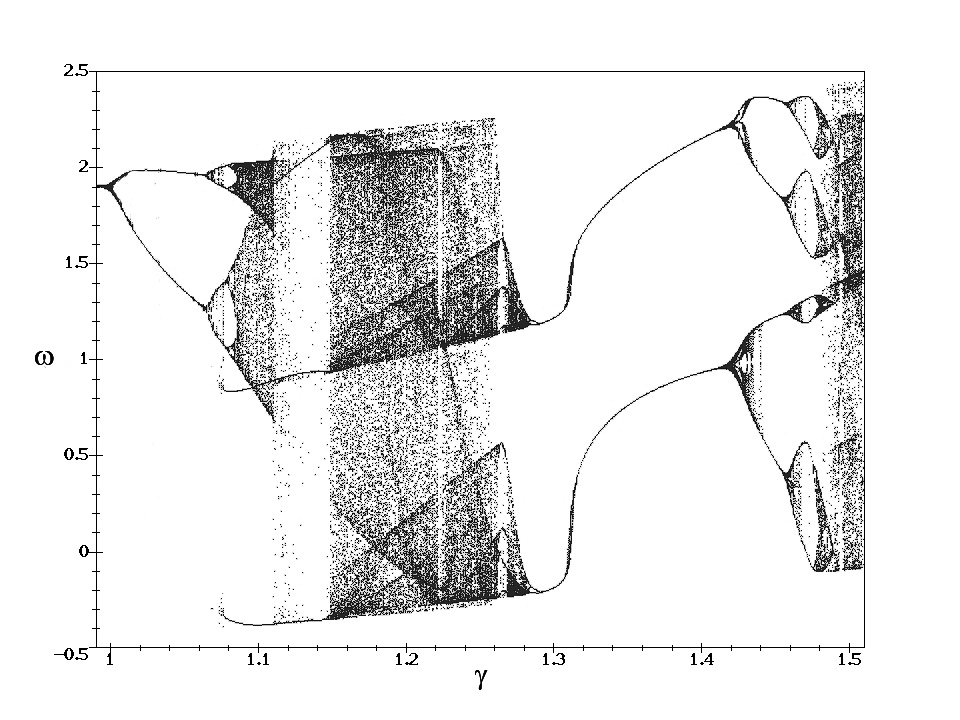
En el dominio con fuerza de accionamiento\(\gamma <1.0663\) hay un ángulo único en cada ciclo de accionamiento como se ilustra en el diagrama de bifurcación. Para una fuerza de transmisión ligeramente mayor, el comportamiento de bifurcación del período dos da como resultado dos ángulos diferentes por ciclo de transmisión. El exponente de Lyapunov es negativo para esta región correspondiente al movimiento ordenado. La cascada de duplicación de período con el aumento en la fuerza de transmisión es fácilmente evidente hasta que el caos se establece en la fuerza de accionamiento crítica\(\gamma _{c}\) cuando hay una distribución aleatoria de velocidades angulares muestreadas y el exponente Lyapunov se vuelve positivo. Tenga en cuenta que en\(\gamma = 1.0845\) hay un breve intervalo de\(6\) movimiento de período seguido de otra región de caos. Alrededor\(\gamma = 1.1\) hay una región que es principalmente caótica que se refleja en valores caóticos de la velocidad angular en la gráfica de bifurcación y grandes valores positivos del exponente Lyapunov. La región alrededor\(\gamma = 1.12\) exhibe el período tres de movimiento y el exponente negativo de Lyapunov correspondiente al movimiento ordenado. La\( 1.15<\gamma <1.25\) región es principalmente caótica y tiene un gran exponente positivo de Lyapunov. La región con\(1.3<\gamma <1.4\) es llamativa en que esto corresponde al movimiento rodante con resurgimiento del periodo uno y exponente negativo de Lyapunov. Este movimiento del período-1 se debe a un movimiento continuo de balanceo del péndulo plano como se muestra en la figura (4.5.3) donde se observa que el promedio\(\theta\) aumenta\(2\pi\) por ciclo, mientras que la velocidad angular\(\omega\) exhibe un movimiento periódico. Es decir, en promedio el péndulo está rotando\(2\pi\) por ciclo. Por encima\(\gamma = 1.4\) del sistema comienzan a exhibir duplicación de período seguido de caos que recuerda el comportamiento visto en\(\gamma\) valores más bajos.

Estos resultados muestran que el diagrama de bifurcación ilustra muy bien el orden de las transiciones de caos para el péndulo armónicamente amortiguado linealmente. Se ve que ocurren varias transiciones entre el orden y el caos. Los regímenes aparentemente ordenados y caóticos son confirmados por los correspondientes exponentes de Lyapunov, los cuales alternan entre valores negativos y positivos para las regiones ordenadas y caóticas respectivamente.

Sección Poincaré

Las parcelas estado-espacio son muy útiles para caracterizar el movimiento periódico, pero se vuelven demasiado densas para una interpretación útil cuando el sistema se acerca al caos como se ilustra en la Figura\(\PageIndex{2}\). Las secciones de Poincaré resuelven esta dificultad tomando una muestra estroboscópica una vez por ciclo del diagrama estado-espacio. Es decir, el punto en la órbita espacial estatal se muestrea una vez por frecuencia de accionamiento. Para periodo-\(1\) movimiento esto corresponde a un solo punto\((\theta ,\omega )\). Para el período-\(2\) movimiento esto corresponde a dos puntos etc. Para los sistemas caóticos, la secuencia de puntos de muestra estado-espacio sigue trayectorias complicadas. La figura\(\PageIndex{3}\) muestra las secciones de Poincaré para el diagrama de espacio de estado correspondiente que se muestra en la figura (4.5.5) para ciclos\(10\) a\(6000\). Tenga en cuenta que las curvas complicadas no se cruzan ni repiten. Las ampliaciones de cualquier parte de esta trama mostrarán trayectorias paralelas cada vez más densas, llamadas fractales, que indican la complejidad del movimiento cíclico caótico. Es decir, al hacer zoom en una pequeña sección de esta trama de Poincaré se muestran muchas trayectorias estrechamente paralelas. Los atractores fractales son sorprendentemente robustos a grandes diferencias en las condiciones iniciales. Las secciones de Poincaré son una sonda sensible de movimiento periódico para sistemas donde el movimiento periódico no es fácilmente aparente.

Figura\(\PageIndex{3}\): Tres parcelas de sección de Poincaré para el péndulo de accionamiento armónico, linealmente amortiguado para diversas condiciones iniciales con\(F_D = 1.2\)\(\tilde\omega = \frac{2}{3}\), y\(\Delta t = \frac{\pi}{100}\). Estos cálculos utilizaron el método Runge-Kutta y fueron realizados por 6000 ciclos por E. Shah (Comunicación privada).

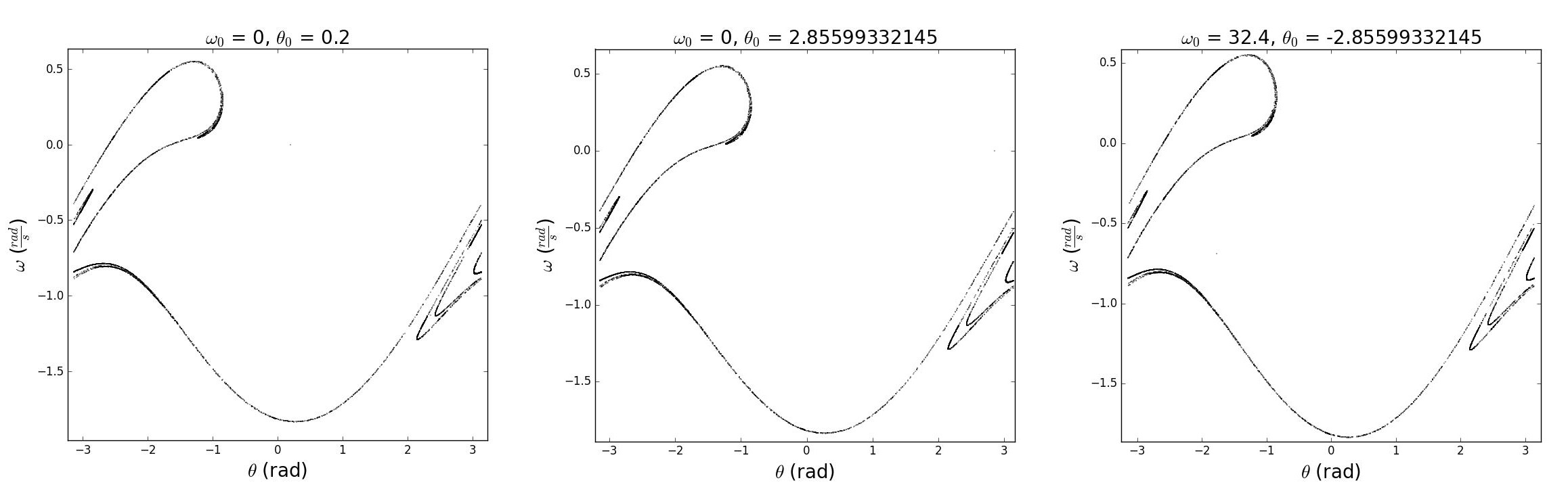
En resumen, el comportamiento del conocido péndulo plano de conducción armónica, amortiguado linealmente, se vuelve notablemente complicado a grandes amplitudes de conducción donde dominan los efectos no lineales. Es decir, cuando la fuerza restauradora es no lineal. El sistema exhibe bifurcación donde puede evolucionar a múltiples atractores que dependen sensiblemente de las condiciones iniciales. El sistema exhibe soluciones oscilatorias y rodantes dependiendo de la amplitud del movimiento. El sistema exhibe dominios de movimiento ordenado simple separados por dominios de movimiento ordenado muy complicado así como regiones caóticas. Las transiciones entre estos modos de movimiento dramáticamente diferentes son extremadamente sensibles a la amplitud y fase del controlador. Eventualmente el movimiento se vuelve completamente caótico. El exponente de Lyapunov, el diagrama de bifurcación y las gráficas de sección de Poincaré, son medidas sensibles del orden del movimiento. Estas tres sensibles medidas de orden y caos se utilizan ampliamente en muchos campos de la mecánica clásica. Se requieren considerables capacidades informáticas para dilucidar el complicado movimiento involucrado en los sistemas no lineales. Los ejemplos incluyen flujo laminar y turbulento en dinámica de fluidos y pronóstico meteorológico de huracanes., donde el movimiento puede abarcar un amplio rango dinámico en dimensiones desde\(10^{-5}\) hasta\(10^{4}\)\(m\).