4.7: Propagación de Ondas para Sistemas No Lineales

Velocidades de fase, grupo y señal

En el capítulo\(3\) se discutió la ecuación de onda y las soluciones para sistemas lineales. Se demostró que, para los sistemas lineales, el movimiento de las olas obedece a superposición y exhibe dispersión, es decir, una velocidad de fase dependiente de la frecuencia y, en algunos casos, atenuación. Los sistemas no lineales introducen intrigantes fenómenos de nueva ola. Por ejemplo, para sistemas no lineales, se deben incluir términos segundo y superiores en la expansión de Taylor dada en la ecuación\((4.2.2)\). Estos términos de segundo y orden superior dan como resultado\( \omega ,\) que la velocidad de grupo sea una función de esto es, la dispersión de la velocidad de grupo ocurre lo que lleva a que la forma de la envolvente del paquete de ondas sea dependiente del tiempo. Como consecuencia, la velocidad de grupo en el paquete de ondas no está bien definida, y no es igual a la velocidad de señal del paquete de ondas o a la velocidad de fase de las ondículas. Los sistemas ópticos no lineales se han estudiado experimentalmente donde\(v_{group}<<c\), lo que se llama luz lenta, mientras que otros sistemas tienen\(v_{group}>c\) lo que se llama luz superluminal. La capacidad de controlar la velocidad de la luz en tales sistemas ópticos es de considerable interés actual ya que tiene aplicaciones de transmisión de señal.

La relación de dispersión para un sistema no lineal se puede expresar como una expansión Taylor de la forma

\[k=k_{0}+\left( \frac{\partial k}{\partial \omega }\right) _{\omega =\omega _{0}}(\omega -\omega _{0})+\frac{1}{2}\left( \frac{\partial ^{2}k}{\partial \omega ^{2}} \right) _{\omega =\omega _{0}}(\omega -\omega _{0})^{2}+..\]

donde\(\omega\) se utiliza como la variable independiente ya que es invariante a las transiciones de fase del sistema. Tenga en cuenta que el factor para el primer término derivado es el recíproco de la velocidad del grupo

\[\left( \frac{\partial k}{\partial \omega }\right) _{\omega =\omega _{0}}\equiv \frac{1}{v_{group}}\]

mientras que el factor para el segundo término derivado es

\[\left( \frac{\partial ^{2}k}{\partial \omega ^{2}}\right) _{\omega =\omega _{0}}=\frac{\partial }{\partial \omega }\left[ \frac{1}{v_{group}(\omega )} \right] _{\omega =\omega _{0}}=\left( -\frac{1}{v_{group}^{2}}\frac{\partial v_{group}}{\partial \omega }\right) _{\omega =\omega _{0}}\]

lo que da la dispersión de velocidad para el sistema.

Desde

\[k=\frac{\omega }{v_{phase}}\]

entonces

\[\frac{\partial k}{\partial \omega }\equiv \frac{1}{v_{group}}=\frac{1}{ v_{phase}}+\omega \frac{\partial \frac{1}{v_{phase}}}{\partial \omega } \label{4.45}\]

Las velocidades inversas para las ondas electromagnéticas se representan mejor en términos de los índices de refracción correspondientes\(n,\) donde

\[n\equiv \frac{c}{v_{phase}}\]

y el índice de refracción del grupo

\[n_{group}\equiv \frac{c}{v_{group}}\]

Entonces la Ecuación\ ref {4.45} se puede escribir en la forma más conveniente\[n_{group}=n+\omega \frac{\partial n}{\partial \omega } \label{4.48}\]

Figura\(\PageIndex{1}\): Las partes real e imaginaria del índice de refracción de fase n más la parte real del índice de refracción grupal asociado a una resonancia atómica aislada.

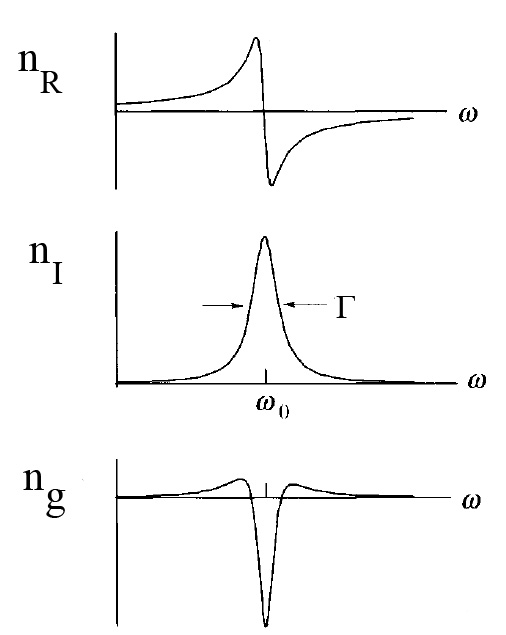
La propagación de ondas para un sistema óptico que está sujeto a una sola resonancia da un ejemplo de respuesta de frecuencia no lineal que tiene aplicaciones a la óptica.

La figura\(\PageIndex{1}\) muestra que las\(n_{I}\) partes real\(n_{R}\) e imaginaria del índice de refracción de fase presentan la dependencia característica de la frecuencia de resonancia del oscilador lineal accionado sinusoidalmente que se discutió en el capítulo\(3.6\) y como se ilustra en la figura (3.6.4). La figura\(\PageIndex{1}\) también muestra el índice de refracción grupal\(n_{group}\) calculado usando la Ecuación\ ref {4.48}.

Obsérvese que en la resonancia,\(n_{group}\) se reduce por debajo del valor no resonante que corresponde a la luz superluminal (rápida), mientras que en las alas de la resonancia\(n_{group}\) es mayor que el valor no resonante correspondiente a la luz lenta. Así, la dependencia no lineal del índice de refracción\(n\) de la frecuencia angular\(\omega\) conduce a velocidades de grupo rápidas o lentas para paquetes de ondas aisladas. Velocidades de la luz tan lentas como se\(17\)\(m/\sec\) han observado. Experimentalmente la absorción de energía que se produce en la resonancia dificulta la observación de la onda electromagnética superluminal en la resonancia.

Obsérvese que Sommerfeld y Brillouin mostraron que aunque la velocidad del grupo pueda superar\(c\), la velocidad de la señal, que marca la llegada del borde de ataque del pulso óptico\(c\), no excede, la velocidad de la luz en vacío, como postuló Einstein.

Propagación de onda solitaria

El solitón es un fenómeno fascinante y muy especial de propagación de ondas que ocurre para ciertos sistemas no lineales. El solitón es un paquete de ondas localizadas solitarias autorreforzantes que mantiene su forma mientras viaja largas distancias a una velocidad constante. Los solitones son causados por una cancelación de la modulación de fase resultante de la dependencia de la velocidad no lineal, y los efectos dispersivos de la velocidad del grupo en un medio. Los solitones surgen como soluciones de una clase extendida de ecuaciones diferenciales parciales dispersivas débilmente no lineales que describen muchos sistemas físicos. La figura\(\PageIndex{2}\) muestra un solitón que comprende una ola de agua solitaria que se aproxima a la costa de Hawai. Mientras que el solitón en la Fig. \(\PageIndex{2}\)puede aparecer como una onda normal, es única en que no hay otras olas que la acompañen. Esta ola probablemente se creó lejos de la costa cuando una ola normal fue modulada por un cambio geométrico en la profundidad del océano, como el fondo marino ascendente, que la obligó a tomar la forma apropiada para un solitón. La ola entonces pudo viajar intacta a la costa, a pesar de la naturaleza aparentemente plácida del océano cerca de la playa. Los solitones son notables en que interactúan entre sí de maneras muy diferentes a las olas normales. Las ondas normales son conocidas por sus complicados patrones de interferencia que dependen de la frecuencia y longitud de onda de las ondas. Los solitones, pueden pasar uno a través del otro sin ser un afectado en absoluto. Esto hace que los solitones sean muy atractivos para los científicos porque las ondas solitónicas son más robustas que las ondas normales y, por lo tanto, pueden usarse para transmitir información de formas que son claramente diferentes a las del movimiento normal de las olas. Por ejemplo, los solitones ópticos se utilizan en fibras ópticas hechas de un medio óptico dispersivo, no lineal, para transmitir pulsos ópticos con una forma invariante.

Figura\(\PageIndex{2}\): Una ola solitaria se acerca a la costa de Hawai. (Imagen: Robert Odom/Universidad de Washington)

Los solitones fueron observados por primera vez\(1834\) por John Scott Russell (\(1808-1882\)). Russell era un ingeniero que realizaba experimentos para aumentar la eficiencia de los barcos del canal. Sus investigaciones experimentales y teóricas le permitieron recrear el fenómeno en tanques de olas. A través de sus extensos estudios, Scott Russell notó que la propagación de solitones exhibía las siguientes propiedades:

• Las olas son estables y mantienen su forma durante largos periodos de tiempo.
• Las olas pueden viajar largas distancias a una velocidad uniforme.
• La velocidad de propagación de la onda depende del tamaño de la ola, con olas más grandes viajando más rápido que las olas más pequeñas.
• Las olas mantuvieron su forma cuando chocaron, aparentemente pasando una a través de la otra.

El trabajo de Scott Russell fue recibido con escepticismo por la comunidad científica. El problema con la Onda de Traducción fue que se trataba de un efecto que dependía de los efectos no lineales, mientras que las teorías de hidrodinámica previamente existentes (como las de Newton y Bernoulli) solo se ocupaban de sistemas lineales. George Biddell Airy, y George Gabriel Stokes, publicaron artículos que atacaban las observaciones de Scott Russell porque las observaciones no podían explicarse por sus teorías de propagación de olas en el agua. Independientemente, Scott Russell estaba convencido de la importancia primordial de la Ola de la Traducción, y la historia demostró que tenía razón. Scott Russell pasó a desarrollar el sistema de “línea de olas” de construcción de cascos que revolucionó la arquitectura naval del siglo XIX, junto con una serie de otros grandes logros que lo llevaron a la fama y el protagonismo. A pesar de todo el éxito en su carrera, continuó a lo largo de su vida para continuar sus estudios de la Ola de la Traducción.

En\(1895\) Korteweg y de Vries desarrollaron una ecuación de olas para olas superficiales para aguas poco profundas.

\[\frac{\partial \phi }{\partial t}+\frac{\partial ^{3}\phi }{\partial x^{3}} +6\phi \frac{\partial \phi }{\partial x}=0\]Una solución de esta ecuación tiene las características de una onda solitaria con forma fija. Se da sustituyendo la forma\(\phi (x,t)=f(x-vt)\) en la ecuación de Korteweg-de Vries que da

\[-v\frac{\partial f}{\partial x}+\frac{\partial ^{3}f}{\partial x^{3}}+6f \frac{\partial f}{\partial x}=0\]Integrando con respecto a\(x\) da

\[3f^{2}+\frac{d^{2}f}{dx^{3}}-cf=C\]

donde\(C\) es una constante de integración. Esta ecuación no lineal tiene una solución

\[\phi (x,t)=\frac{1}{2}c\sec h^{2}\left[ \frac{\sqrt{v}}{2}(x-vt-a)\right] \label{4.52}\]

donde\(a\) es una constante. La ecuación\ ref {4.52} es la ecuación de una onda solitaria que se mueve en la\(+x\) dirección a una velocidad\(v\).

El comportamiento solitón se observa en fenómenos como tsunamis, perforaciones de marea que ocurren en algunos ríos, señales en fibras ópticas, plasmas, ondas atmosféricas, filamentos de vórtice, superconductividad y campos gravitacionales con simetría cilíndrica. Se ha trabajado mucho en solitones para aplicaciones de fibra óptica. La estabilidad inherente del solitón hace posible la transmisión a larga distancia sin el uso de repetidores, y potencialmente podría duplicar la capacidad de transmisión.

Antes del descubrimiento de los solitones, los matemáticos tenían la impresión de que las ecuaciones diferenciales parciales no lineales no podían resolverse exactamente. Sin embargo, los solitones llevaron al reconocimiento de que existen sistemas no lineales que pueden resolverse analíticamente. Este descubrimiento ha provocado mucha investigación sobre estos llamados “sistemas integrables”. Dichos sistemas son raros, ya que la mayoría de las ecuaciones diferenciales no lineales admiten un comportamiento caótico sin soluciones explícitas. Sin embargo, los sistemas integrables conducen a matemáticas muy interesantes que van desde la geometría diferencial y el análisis complejo hasta la teoría cuántica de campos y la dinámica de fluidos

Muchas de las ecuaciones fundamentales en física (Maxwell, Schrödinger) son ecuaciones lineales. Sin embargo, los físicos han comenzado a reconocer muchas áreas de la física en las que la no linealidad puede dar como resultado un fenómeno cualitativamente nuevo que no se puede construir a través de la teoría de la perturbación a partir de ecuaciones linealizadas. Estos incluyen fenómenos en magnetohidrodinámica, meteorología, oceanografía, física de la materia condensada, óptica no lineal y física de partículas elementales. Por ejemplo, la misión espacial europea Clúster detectó perturbaciones eléctricas similares a solitones que viajaban a través del gas ionizado que rodeaba la Tierra a partir de unos 50 mil kilómetros de la Tierra y viajaban hacia el planeta a unos 8 km/s Se piensa que este solitón fue generado por la turbulencia en la magnetosfera.

Los esfuerzos por comprender la no linealidad de los solitones han llevado a mucha investigación en muchas áreas de la física. En el contexto de los solitones, su comportamiento similar a partículas (en el sentido de que se localizan y conservan bajo colisiones) conduce a una serie de aplicaciones experimentales y teóricas. La técnica conocida como bosonización permite visualizar partículas, tales como electrones y positrones, como solitones en ecuaciones de campo apropiadas. Existen numerosos fenómenos macroscópicos, como las ondas internas en el océano, la transparencia espontánea y el comportamiento de la luz en el cable de fibra óptica, que ahora se entienden en términos de solitones. Estos fenómenos se están aplicando a la tecnología moderna.