6.9: Aplicaciones que involucran restricciones no holonómicas
- Page ID
- 126605
En general, las restricciones no holonómicas pueden manejarse mediante el uso de fuerzas generalizadas\(Q_{j}^{EXC}\) en las ecuaciones de Lagrange-Euler\((6.5.12)\). Los siguientes ejemplos,\(\PageIndex{1}-\PageIndex{4}\), involucran restricciones unilaterales que exhiben un comportamiento holonómico para rangos restringidos de la superficie de restricción en el espacio de coordenadas, y este rango es específico de cada caso. Cuando las fuerzas de restricción presionan el objeto contra la superficie de restricción, entonces el sistema es holonómico, pero el rango holonómico del espacio de coordenadas se limita a situaciones en las que las fuerzas de restricción son positivas. Cuando la fuerza de restricción es negativa, el objeto se libera de la superficie de restricción. Además, cuando la fuerza de fricción\(F>N\mu _{static}\) donde\(\mu _{static}\) es el coeficiente estático de fricción, entonces el objeto se desliza negando cualquier restricción de rodadura que asuma fricción estática.
Ejemplo\(\PageIndex{1}\): Mass sliding on a frictionless spherical shell
Considere que una masa comienza desde el reposo en la parte superior de una concha esférica fija sin fricción de radio\(R\). Las preguntas son cuál es la fuerza de restricción y determinar el ángulo\(\theta\) en el que la masa sale de la superficie de la concha esférica. Las coordenadas\(r,\theta\) mostradas son las coordenadas generalizadas obvias a usar.
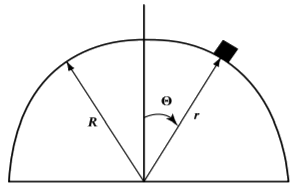
La restricción no se aplicará si la fuerza de restricción no mantiene la masa contra la superficie de la concha esférica, es decir, solo es holonómica en un dominio restringido.
\[L= \frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{\theta}^{2}\right) -mgr\cos \theta \nonumber\]
Este lagrangiano es aplicable independientemente de que se obedezca la restricción, donde la restricción viene dada por\[g(r,\theta )=r-R=0\nonumber\]
Para el dominio restringido donde este sistema es holonómico, se puede resolver usando coordenadas generalizadas, fuerzas generalizadas, multiplicadores Lagrange o mecánica newtoniana como se ilustra a continuación.
Coordenadas mínimas generalizadas:
El número mínimo de coordenadas generalizadas reduce el sistema a una coordenada\(\theta\), lo que no determina la fuerza de restricción que se necesita para saber si se aplica la restricción. Por lo tanto, este enfoque no es útil para resolver este sistema parcial-holonómico.
Fuerzas generalizadas:
\[F=Q_{r}=mg(3\cos \theta -2)\nonumber\]
Tenga en cuenta que\(F=Q_{r}=0\) cuando\(\cos \theta =\frac{2}{3}\), es decir\(\theta =48.2^{o}.\)
Multiplicadores Lagrange:
\[m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2}=\lambda \tag{a}\]
La ecuación de Lagrange para\(\theta\) da\(\Delta _{\theta }L=\lambda \frac{\partial g}{\partial \theta }=0\) desde\(\frac{\partial g}{\partial \theta }=0.\) Así\[mr^{2}\ddot{\theta}-mgr\sin \theta +2mr\dot{r}\dot{\theta}=0 \tag{b} \label{b2}\]
\[\dot{\theta}^{2}=\frac{2g}{R}\left( 1-\cos \theta \right) \tag{d} \label{d2}\]
asumiendo que\(\dot{\theta}=0\) en\(\theta =0.\)
\[F=\lambda =mg(3\cos \theta -2)\nonumber\]
Tenga en cuenta que\(\lambda =0\) cuando\(\cos \theta =\frac{2}{3}\), es decir\(\theta =48.2^{o}.\)
Ambos métodos anteriores dan resultados idénticos y dan que la fuerza de restricción es negativa cuando\(\theta >48.2^{o}.\) Asumiendo que la superficie no puede retener la masa contra la superficie, entonces la masa volará fuera de la concha esférica cuando\(\theta >48.2^{o}\) y el sistema se reduzca a un objeto sin restricciones que caiga libremente en un campo gravitacional uniforme, que es holonómico, es decir\(Q_{r}=\lambda =0.\) Entonces las ecuaciones de movimiento\(\left( a\right)\) y\((b)\) reducir a\[\begin{align} m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2} &=&0 \tag{e} \\ mr^{2}\ddot{\theta}-mgr\sin \theta +2mr\dot{r}\dot{\theta} &=&0 \tag{f}\end{align}\]
Conservación de energía:
\[\frac{v^{2}}{R}=2g[1-\cos \theta ]=g\cos \theta\nonumber\]
Esto ocurre cuando\(\cos \theta =\frac{2}{3}\). Se trata de un caso inusual donde el enfoque newtoniano es el más sencillo.
Ejemplo\(\PageIndex{2}\): Rolling solid sphere on a spherical shell
Este es un problema similar al anterior con la complicación añadida de rodar que se supone que se mueve en un plano vertical haciéndola holonómica. Aquí nos gustaría determinar las fuerzas de restricción para ver cuándo la esfera sólida vuela de la concha esférica y cuando la fricción es insuficiente para evitar que la esfera rodante se deslice.
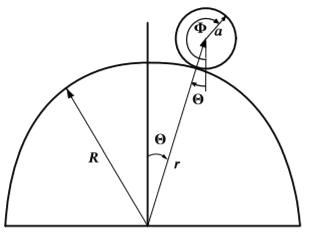
Las mejores coordenadas generalizadas son la distancia del centro de la esfera desde el centro de la concha esférica,\(r,\theta\) y\(\phi .\) es importante señalar que\(\phi\) se mide con respecto a la vertical, no al vector dependiente del tiempo\(\mathbf{r}\). Es decir, la dirección del radio\(r\) es la\(\theta\) que depende del tiempo y por lo tanto no es una referencia útil para usar para definir el ángulo\(\phi\). Supongamos que la esfera es uniforme con un momento de inercia de\(I= \frac{2}{5}ma^{2}.\) Si la fuerza tangencial de fricción\(F\) es menor que el valor limitante\(N\mu _{statics}\), con\(N>0,\) entonces la esfera rodará sin deslizarse sobre la superficie del cilindro y se aplicarán ambas restricciones. Bajo estas condiciones el sistema es holonómico y la solución se resuelve utilizando multiplicadores Lagrange y las ecuaciones de restricción son las siguientes:
- El centro de la esfera sigue la superficie del cilindro\[g_{1}=r-R-a=0\nonumber\]
- La esfera rueda sin resbalar\[g_{2}=a\left( \phi -\theta \right) -R\theta =0\nonumber\]
La energía cinética es\(T=\frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{ \theta}^{2}\right) +\frac{1}{2}I\dot{\phi}^{2}\) y la energía potencial es\(U=mgr\cos \theta .\) Así el Lagrangiano es\[L=\frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{\theta}^{2}\right) +\frac{1}{2}I \dot{\phi}^{2}-mgr\cos \theta\nonumber\]
\[mr^{2}\ddot{\theta}+2mr\dot{r}\dot{\theta}-mgr\sin \theta =-\lambda _{2}\left( R+a\right) \tag{b} \label{b3}\]
\(\Lambda _{\phi }L\)da\[I\ddot{\phi}=a\lambda _{2} \tag{c}\]
\[\cos \theta =\frac{10}{17}\nonumber\]
Para ángulos más grandes\(\lambda _{1}\) es negativo, lo que implica que la esfera sólida volará de la superficie de la concha esférica.
La esfera saldrá de la superficie del cilindro cuando es\(\cos \theta =\frac{10}{17}\) decir,\(\theta =53.97^{o}.\) Este es un ángulo significativamente mayor que el obtenido para el problema similar donde la masa se desliza sobre un cilindro sin fricción debido a que la energía almacenada en rotación implica que la velocidad lineal de la masa es menor a un ángulo dado\(\theta\) para el caso de una esfera rodante.
\[F_{f}=-\lambda _{2}\nonumber\]
Está en la dirección negativa debido a la dirección elegida para\(\phi .\) El coeficiente de fricción requerido\(\mu\) viene dado por la relación de la fuerza de fricción a la fuerza normal, es decir\[\mu =\frac{\lambda _{2}}{\lambda _{1}}=\frac{2\sin \theta }{\left[ 17\cos \theta -10\right] }\nonumber\]
Para\(\mu =1\) el disco comienza a deslizarse cuando\(\theta =47.54^{0}.\) Tenga en cuenta que la esfera comienza a deslizarse antes de que salga volando del cilindro ya que se requiere una fuerza normal para soportar una fuerza de fricción y la diferencia depende del coeficiente de fricción. La restricción de no deslizamiento no se satisface una vez que la esfera comienza a deslizarse y la fuerza de fricción debe ser igual.\(\mu _{kinetic}\lambda _{1}.\) Por lo tanto, para\(47.54^{o}\) los ángulos más allá del problema necesita resolverse con la restricción de rodadura cambiada a una fuerza de fricción deslizante no conservadora. Esto se maneja mejor al incluir la fuerza de fricción y las fuerzas normales como fuerzas generalizadas. Afortunadamente esta será una pequeña corrección. La fricción cambiará ligeramente el ángulo exacto en el que la fuerza normal se convierte en cero y el sistema pasa al movimiento libre de la esfera en un campo gravitacional.
Ejemplo\(\PageIndex{3}\): Solid sphere rolling plus slipping on a spherical shell
\[F=N\mu _{sliding}\nonumber\]
cuando\(N\) es positivo.
\[\frac{d}{dt}\frac{\partial L}{\partial \dot{r}}-\frac{\partial L}{\partial r} =Q_{r}=N\nonumber\]
lo que da\[m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2}=N\nonumber\]
\[mr^{2}\ddot{\theta}+2mr\dot{r}\dot{\theta}-mgr\sin \theta =-F\left( R+a\right)\nonumber\]
Del mismo modo\(\Lambda _{\phi }L=Q_{\phi }=aF\) da\[I\ddot{\phi}=aF\nonumber\]
Estos pueden resolverse sustituyendo la relación\(F=N\mu _{sliding}\). La esfera vuela fuera de la concha esférica cuando\(N\leq 0\) conduce al libre movimiento discutido en el ejemplo\((7.7.2)\). El problema de que una esfera sólida y uniforme ruede dentro de una esfera hueca se puede resolver de la misma manera.
Ejemplo\(\PageIndex{4}\): Small body held by friction on the periphery of a rolling wheel
Supongamos que un pequeño cuerpo de masa\(m\) se equilibra sobre una rueda rodante de masa\(M\) y radio\(R\) como se muestra en la figura. La rueda rueda en un plano vertical sin deslizarse sobre una superficie horizontal. Este ejemplo ilustra que es posible utilizar simultáneamente una mezcla de restricciones holonómicas, restricciones parcialmente-holonómicas y fuerzas generalizadas. 3
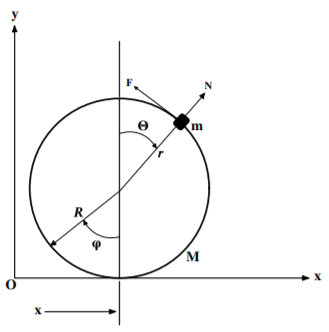
Supongamos que\(t=0\) al volante toca el piso en\(x=y=0\) con la masa encaramada en la parte superior de la rueda en\(x=0\). Deje que la fuerza de fricción que actúa sobre la masa\(m\) sea\(F\) y la fuerza de reacción de la periferia de la rueda sobre la masa sea\(N\). Dejar\(\dot{\varphi}\) ser la velocidad angular de la rueda, y\(\dot{x}\) la velocidad horizontal del centro de la rueda. Las coordenadas polares\(r,\theta\) de la masa\(m\) se toman con\(r\) medidas desde el centro de la rueda con\(\theta\) medidas con respecto a la vertical. Así, las coordenadas cartesianas de la masa pequeña\(m\) son\((x+r\sin \theta ,R+r\cos \theta )\) con respecto al origen at\(x=y=0\).
\[U=+mg\left( R+r\cos \theta \right)\nonumber\]
Así el lagrangiano es\[L=\frac{1}{2}\left( M+m\right) \dot{x}^{2}+\frac{1}{2}I\dot{\varphi}^{2}+ \frac{1}{2}m\left[ r^{2}\dot{\theta}^{2}+2r\dot{x}\dot{\theta}\cos \theta +2 \dot{x}\dot{r}\sin \theta +\dot{r}^{2}\right] -mg\left( R+r\cos \theta \right)\nonumber\]
Las ecuaciones de restricciones son:
1) La rueda rueda sin deslizarse sobre el plano de tierra, lo que lleva a una restricción holonómica:\[g_{1}=x-R\varphi =\dot{x}-R\dot{\varphi}=0\]
2) La masa\(m\) está tocando la periferia de la rueda, es decir, la fuerza normal\(N>0.\) Esta es una restricción holonómica restringida unilateral. \[g_{2}=R-r=0\nonumber\]
3) La masa\(m\) no se desliza sobre la rueda si la fuerza de fricción\(F<\)\(N\mu _{static}\). Cuando se satisface esta restricción holonómica restringida, entonces\[g_{3}=\dot{\theta}-\dot{\varphi}=0\]
La restricción rodante es holonómica y se puede explicar usando un multiplicador de Lagrange\(\lambda _{x}\) más las ecuaciones de restricción diferencial
\[m\ddot{x}\sin \theta +mR\dot{\theta}^{2}-mg\cos \theta +N=0\nonumber\]
Esta última ecuación puede ser derivada por la mecánica newtoniana a partir de la consideración de las fuerzas que actúan.
Las ecuaciones de movimiento anteriores se pueden utilizar para calcular el movimiento para las siguientes condiciones.
a) Masa que no se deslice:
Esto ocurre si\(\mu =\frac{F}{N}\leq \mu _{static}\) lo que implica también que\(N>0,\) Esa es una situación en la que el sistema es holonómico con\(r=R,\)\(\dot{x}=R\dot{\varphi},\)\(\dot{ \theta}=\dot{\varphi}\) lo que se puede resolver utilizando el enfoque de coordenadas generalizadas con una sola coordenada independiente que se puede tomar para ser\(\theta\).
b) Deslizamiento masivo:
Aquí se viola la restricción antideslizante y por lo tanto hay que incluir explícitamente las fuerzas generalizadas\(Q_{r},Q_{\varphi },Q_{\theta }\) y asumir que la fricción deslizante viene dada por\(F=N\mu _{sliding}.\)
c) La fuerza de reacción\(N\) es negativa:
Aquí la masa no está sujeta a ninguna restricción y está en caída libre.
El ejemplo anterior ilustra la flexibilidad proporcionada por la mecánica lagrangiana que permite el uso simultáneo de multiplicadores Lagrange, fuerzas generalizadas y potencial escalar para manejar combinaciones de varias restricciones holonómicas y no holonómicas para un problema complicado.
3 Este problema se resuelve en detalle en el ejemplo 3.19 de “Mecánica Clásica y Relatividad”. por Muller-Kirsten\(\left[ Mu06\right] \).

