6.8: Aplicaciones a sistemas que involucran restricciones holonómicas

Las ecuaciones de movimiento que resultan del enfoque algebraico Lagrange-Euler son las mismas que las dadas por la mecánica newtoniana. La solución de estas ecuaciones de movimiento se puede obtener matemáticamente usando las condiciones iniciales elegidas. El siguiente ejemplo simple de un disco rodando sobre un plano inclinado, es útil para comparar los méritos del método newtoniano con la mecánica de Lagrange empleando coordenadas mínimas generalizadas, los multiplicadores Lagrange o los enfoques de fuerzas generalizadas.

Ejemplo\(\PageIndex{1}\): Disk rolling on an inclined plane

Figura\(\PageIndex{1}\): Rolling de discos sin deslizarse sobre un plano inclinado.

Restricción rodante da

\[y - R \theta = 0 \nonumber\]

\[x-R=0\nonumber\]

a) Las leyes del movimiento de Newton

\[\left( m+\frac{I}{R^{2}}\right) \ddot{y}-mg\sin \alpha =0\nonumber\]

El momento de inercia de un disco circular sólido uniforme es\(I=\frac{1 }{2}mR^{2}\)

\[F_{f}=\frac{mg}{3}\sin \alpha\nonumber\]

que es menor que la fuerza gravitacional a lo largo del plano que es\(mg\sin \alpha .\)

b) Ecuaciones de Lagrange con un conjunto mínimo de coordenadas generalizadas

\[mg\sin \alpha =\left( m+\frac{I}{R^{2}}\right) \overset{..}{y}\nonumber\]

De nuevo si\(I=\frac{1}{2}mR^{2}\) entonces\[\ddot{y}=\frac{2}{3}g\sin \alpha\nonumber\]

La solución para la\(x\) coordenada es trivial. Esta respuesta es idéntica a la obtenida usando las leyes del movimiento de Newton. Obsérvese que no se han determinado fuerzas utilizando la coordenada generalizada única.

c) Ecuación de Lagrange con multiplicadores Lagrange

\[m\ddot{y}=mg\sin \alpha +\lambda _{1}=\frac{2}{3}mg\sin \alpha\nonumber\]

y el par es\[-\lambda _{1}R=F_{f}R=I\ddot{\theta}\nonumber\]

d) Ecuación de Lagrange usando una fuerza generalizada

\[\begin{aligned} Q_{y} &=&-F_{f} \\ Q_{\theta } &=&F_{f}R\end{aligned} \]

Las ecuaciones de Euler-Lagrange son:

\[F_{f}=-\frac{mg}{3}\sin \alpha\nonumber\]

Los cuatro métodos para manejar las ecuaciones de restricción son todos equivalentes y dan como resultado las mismas ecuaciones de movimiento. La mecánica lagrangiana escalar es capaz de calcular las fuerzas vectoriales que actúan de manera directa y sencilla. El enfoque de la ley de Newton es más intuitivo para este simple caso y la facilidad y el poder del enfoque lagrangiano no es evidente para este sencillo sistema.

La siguiente serie de ejemplos aumentará gradualmente en complejidad, e ilustrarán el poder, la elegancia, más la superioridad del enfoque lagrangiano en comparación con el enfoque newtoniano.

Ejemplo\(\PageIndex{2}\): Two connected masses on frictionless inclined planes

Figura\(\PageIndex{2}\): Dos masas conectadas en planos inclinados sin fricción

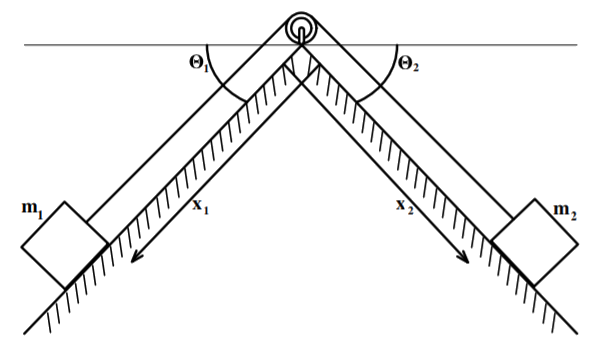
\[T= \frac{1}{2}m_{1}\dot{x}_{1}^{2}+\frac{1}{2}m_{2}\dot{x}_{2}^{2}=\frac{1}{2} \left( m_{1}+m_{2}\right) \dot{x}_{1}^{2}\nonumber\]

El lagrangiano da entonces que

\[L=\frac{1}{2}\left( m_{1}+m_{2}\right) \dot{x}_{1}^{2}+m_{1}gx_{1}\sin \theta _{1}+m_{2}g\left( l-x_{1}\right) \sin \theta _{2}\nonumber\]

Por lo tanto\[\begin{aligned} \frac{\partial L}{\partial \dot{x}_{1}} &=&\left( m_{1}+m_{2}\right) \dot{x} _{1} \\ \frac{\partial L}{\partial x_{1}} &=&g\left( m_{1}\sin \theta _{1}-m_{2}\sin \theta _{2}\right)\end{aligned} \]

\[\Lambda _{x_{1}}L=\frac{d}{dt}\frac{\partial L}{\partial \dot{x}_{1}}-\frac{ \partial L}{\partial x_{1}}=0=\left( m_{1}+m_{2}\right) \ddot{x}_{1}-g\left( m_{1}\sin \theta _{1}-m_{2}\sin \theta _{2}\right)\nonumber\]

Tenga en cuenta que el sistema actúa como si la masa inercial estuviera\((m_{1}+m_{2})\) mientras que la fuerza impulsora proviene de la diferencia de las fuerzas. La aceleración es cero si

\[m_{1}\sin \theta _{1}=m_{2}\sin \theta _{2}\nonumber\]

\[\left( m_{1}+m_{2}\right) \ddot{x}_{1}=g\left( m_{1}-m_{2}\right)\nonumber\]

Tenga en cuenta que este problema se ha resuelto sin ninguna referencia a la fuerza en la cuerda o las fuerzas de restricción normales en los planos inclinados.

Ejemplo\(\PageIndex{3}\): Block sliding on a movable frictionless inclined plane

Figura\(\PageIndex{3}\): Un bloque que se desliza sobre un plano inclinado móvil sin fricción.

El Lagrangiano es\[L=\frac{1}{2} M \dot{x}^{2}+\frac{1}{2} m\left[\dot{x}^{2}+\dot{x}^{\prime 2}+2 \dot{x} \dot{x}^{\prime} \cos \theta\right]+m g x^{\prime} \sin \theta\nonumber\]

Considere la ecuación de Lagrange-Euler para la\(x\) coordenada,\(\Lambda_x L = 0\) que da

\[\frac{d}{dt}[m(\dot{x}+\dot{x}^{\prime }\cos \theta )+M\dot{x}]=0 \tag{$a$} \label{a2}\]

que afirma que\([m(\dot{x}+\dot{x}^{\prime }\cos \theta )+M\dot{x }]\) es una constante de movimiento. Esta constante de movimiento es solo el impulso lineal total del sistema completo en la\(x\) dirección. Es decir, la conservación del impulso lineal se satisface automáticamente por el enfoque lagrangiano. El enfoque newtoniano también predice la conservación del impulso lineal ya que no hay fuerzas horizontales externas,

Considere la ecuación de Lagrange-Euler para la\(x^{\prime}\) coordenada,\(\Lambda_{x^{\prime}} L = 0\) que da

\[\ddot{x}^{\prime }=\frac{g\sin \theta }{1-m\cos ^{2}\theta /(m+M)}\nonumber\]

Este ejemplo ilustra la flexibilidad de poder usar vectores de desplazamiento no ortogonales para especificar la energía lagrangiana escalar. La mecánica newtoniana requeriría más pensamiento para resolver este problema.

Ejemplo\(\PageIndex{4}\): Sphere rolling without slipping down an inclined plane on a frictionless floor

\[\begin{aligned} v_{x} &=& \dot{x}+R\dot{\theta}\cos \varphi \\ v_{y} &=&-R\dot{\theta}\sin \varphi\end{aligned} \]

Supongamos que las condiciones iniciales son\(t=0,\xi =0,x=0,\theta =0,y=h,\dot{x}= \dot{\theta}=0.\) Elegir las coordenadas independientes\(x\) y\(\theta\) como coordenadas generalizadas más la restricción holonómica\(\xi =R\theta\). Entonces el lagrangiano es\[L=\frac{M}{2}\dot{x}^{2}+\frac{m}{2}\left[ \dot{x}^{2}+r^{2}\dot{\theta} ^{2}+2r\dot{x}\dot{\theta}\cos \varphi \right] +\frac{m}{5}r^{2}\dot{\theta} ^{2}-mg\left( h-r\theta \sin \varphi \right)\nonumber\]

Figura\(\PageIndex{4}\): Esfera sólida rodando sin deslizarse sobre un plano inclinado sobre un piso horizontal sin fricción.

\[x=-\frac{mr\cos \varphi }{M+m}\theta =\frac{5m\sin \left( 2\varphi \right) }{ 4\left[ 7\left( M+m\right) -5m\cos ^{2}\varphi \right] }gt^{2}\nonumber\]

Tenga en cuenta que estas ecuaciones predicen la conservación del momento lineal para el bloque más esfera.

Ejemplo\(\PageIndex{5}\): Mass sliding on a rotating straight frictionless rod.

Figura\(\PageIndex{5}\): Masa deslizante sobre una varilla recta giratoria sin fricción.

\[\Lambda _{\theta }L=\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}- \frac{\partial L}{\partial \theta }=\frac{d}{dt}(mr^{2}\dot{\theta})=0\nonumber\]

Por lo tanto, el momento angular es constante\[mr^{2}\dot{\theta}=\text{constant}=p_{\theta }\nonumber\]

La ecuación de Lagrange para\(r\) da\[\Lambda _{r}L=\frac{d}{dt}\frac{\partial L}{\partial \dot{r}}-\frac{\partial L}{\partial r}=m\ddot{r}-mr\dot{\theta}^{2}=0\nonumber\]

La\(\theta\) ecuación establece que el momento angular se conserva para este caso que es lo que esperamos ya que no hay pares externos que actúen sobre el sistema. La\(r\) ecuación establece que la aceleración centrífuga es\(\ddot{r}=r\omega ^{2}.\) Estas ecuaciones de movimiento se derivaron sin referencia a las fuerzas entre la varilla y la masa.

Ejemplo\(\PageIndex{6}\): Spherical pendulum

Figura\(\PageIndex{6}\): Péndulo esférico

\[U=-mgb\cos \theta\nonumber\]

dando que\[L=\frac{1}{2}mb^{2}\dot{\theta}^{2}+\frac{1}{2}mb^{2}\sin ^{2}\theta \dot{ \phi}^{2}+mgb\cos \theta\nonumber\]

\[mb^{2}\sin ^{2}\theta \dot{\phi}=p_{\phi }=\text{ constant}\nonumber\]

Esto es solo el momento angular\(p_{\phi }\) para que el péndulo gire en la\(\phi\) dirección. Automáticamente, el enfoque de Lagrange muestra que el momento angular\(p_{\phi }\) es una cantidad conservada. Esto es lo que se espera de las Leyes del Movimiento de Newton ya que no hay pares externos aplicados alrededor de este eje vertical.

La ecuación de movimiento para se\(\theta\) puede simplificar a\[\ddot{\theta}+\frac{g}{b}\sin \theta -\frac{p_{\phi }^{2}\cos \theta }{ m^{2}b^{4}\sin ^{3}\theta }=0\nonumber\]

Existen muchas soluciones posibles dependiendo de las condiciones iniciales. El péndulo puede simplemente oscilar en la\(\theta\) dirección, o girar en la\(\phi\) dirección o alguna combinación de estos. Obsérvese que si\(p_{\phi }\) es cero, entonces la ecuación se reduce al péndulo armónico simple, mientras que el otro extremo es cuando\(\ddot{\theta}=0\) para el cual el movimiento es el de un péndulo cónico que gira en ángulo constante con respecto\(\theta _{0}\) al eje vertical.

Ejemplo\(\PageIndex{7}\): Mass constrained to move on the inside of a frictionless paraboloid

Figura\(\PageIndex{7}\): Masa restringida para deslizarse en el interior de un paraboloide sin fricción.

\[x^{2}+y^{2}=\rho ^{2}=az\nonumber\]

con una energía potencial gravitacional de\(U=mgz.\)

Este sistema es holonómico, escleronómico y conservador. Elija coordenadas cilíndricas\(\rho ,\phi ,z\) con respecto al eje vertical del paraboloide para ser las coordenadas generalizadas.

\[g(\rho ,z)=\rho ^{2}-az=0\nonumber\]

Se utilizará el enfoque multiplicador de Lagrange para determinar las fuerzas de restricción.

Para\(\Lambda _{\rho }L=\lambda \frac{\partial g}{\partial \rho }\)

\[\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot{r}}-\frac{\partial L}{\partial r} &=&\lambda _{1}2\rho \tag{a} \label{a3} \\ m\left( \ddot{\rho}-\rho \dot{\phi}^{2}\right) &=&\lambda _{1}2\rho \notag\end{align}\]

Para\(\Lambda _{\phi }L=\lambda \frac{\partial g}{\partial \phi }\)

\[\frac{d}{dt}\left( m\rho ^{2}\dot{\phi}\right) =\dot{p}_{\phi }=0 \tag{b} \label{b3}\]

Así\(p_{\phi }\) se conserva el momento angular, es decir, es una constante de movimiento.

\[2\rho \dot{\rho}-a\dot{z}=0 \tag{d} \label{d3}\]

Las cuatro ecuaciones de movimiento anteriores se pueden utilizar para determinar\(r,\phi .z,\lambda _{1}.\)

\[F_{c}=\lambda _{1}\frac{\partial g(\rho ,z)}{\partial \rho }=-\frac{mg}{a} 2\rho\nonumber\]

Suponiendo que\(\ddot{\rho}=0,\) entonces la ecuación\ ref {a3} para\(\dot{\phi}=\omega\) y\(\rho =\rho _{0}\) da

\[F_{c}=-m\rho _{0}\omega ^{2}\nonumber\]

que es la fuerza centrípeta habitual. Estas relaciones también dan que la velocidad angular inicial requerida para una trayectoria tan estable con altura\(h\) es\[{\small \ }\dot{\phi}=\omega =\sqrt{\frac{2g}{a}}\nonumber\]

Ejemplo\(\PageIndex{8}\): Mass on a frictionless plane connected to a plane pendulum

Figura\(\PageIndex{8}\): Masa\(m_2\), colgada de una cuerda a la que se conecta\(m_1\), la cual se desliza sobre un plano sin fricción.

Dos masas\(m_{1}\) y\(m_{2}\) están conectadas por una cadena de longitud\(l\). \(m_{1}\)La masa está sobre una mesa horizontal sin fricción y se supone que la masa\(m_{2}\) se mueve en un plano vertical. Este es otro problema que involucra el movimiento holonómico restringido. Las limitaciones son:

1)\(m_{1}\) se mueve en el plano horizontal

2)\(m_{2}\) se mueve en el plano vertical

3)\(r+s=l.\) Por lo tanto\(\dot{r}=-\dot{s}\)

Así, las ecuaciones de Lagrange son

\ [\ begin {alineado} &\ lambda_ {r} L=\ izquierda (m_ {1} +m_ {2}\ derecha)\ ddot {r} +m_ {1} (l-r)\ punto {\ phi} ^ {2} -m_ {2} r\ punto {\ theta} ^ {2} -m_ {2} g\ cos\ theta=0\ &
\ Lambda_ {\ theta} L=\ frac {d} {d t}\ izquierda [m_ {2} r^ {2}\ punto {\ theta}\ derecha] +m_ {2} g r\ sin\ theta=0\ end {alineado}\]

es decir

\[2 m_{2} \dot{r} \dot{\theta}+r^{2} m_{2} \ddot{\theta}+m_{2} g r \sin \theta=0 \nonumber\]

\[\Lambda _{\phi }L=\frac{d}{dt}\left[ m_{1}\left( l-r\right) ^{2}\dot{\phi} \right] =0\nonumber\]

Esta última ecuación es una declaración de la conservación del momento angular. Estas tres ecuaciones diferenciales de movimiento se pueden resolver para condiciones iniciales conocidas.

Ejemplo\(\PageIndex{9}\): Two connected masses constrained to slide along a moving rod

Figura\(\PageIndex{9}\): Dos masas idénticas\(m\) restringidas a deslizarse sobre una varilla de masa móvil\(M\). Las masas están unidas al centro de la varilla por resortes idénticos, cada uno de los cuales tiene una constante de resorte\(K\).

Considere dos masas idénticas\(m,\) restringidas para moverse a lo largo del eje de una varilla recta delgada, de masa\(M\) y longitud\(l,\) que es libre tanto para trasladarse como para rotar. Dos muelles idénticos unen las dos masas al punto central de la varilla. Considera solo los movimientos del sistema para los cuales las longitudes extendidas de los dos resortes son iguales y opuestas de tal manera que las dos masas siempre están a distancias iguales del centro de la varilla manteniendo el centro de masa en el centro de la varilla. Encuentra las ecuaciones de movimiento para este sistema.

Utilice un sistema de coordenadas cartesianas fijas\((x,y,z)\) y un marco móvil con el origen\(O\) en el centro de la varilla con sus coordenadas\((x_{1},y_{1},z_{1})\) cartesianas paralelas al marco de coordenadas fijas como se muestra en la figura. Dejan\((r,\theta ,\varphi )\) ser las coordenadas esféricas de un punto refiriéndose al centro del\((x_{1},y_{1},z_{1})\) marco móvil como se muestra en la figura. Entonces las dos masas\(m\) tienen coordenadas esféricas\((r,\theta ,\varphi )\) y\((-r,\theta ,\varphi )\) en el marco fijo de varilla móvil. Las restricciones sin fricción son holonómicas.

\[L=\frac{1}{2}(M+2m)(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})+m(\dot{r}^{2}+r^{2} \dot{\theta}^{2}+r^{2}\dot{\varphi}^{2}\sin ^{2}\theta )+\frac{1}{24}ML^{2}( \dot{\theta}^{2}+\dot{\varphi}^{2}\sin ^{2}\theta )-K(r-r_{0})^{2}\nonumber\]

Usando las ecuaciones de Lagrange\(\Lambda _{q_{i}}L=0\) para las coordenadas generalizadas da.

\[\begin{align} (M+2m)\dot{x} &=&\text{constant} \tag{$\Lambda _{x}L=0$} \\ (M+2m)\dot{y} &=&\text{constant} \tag{$\Lambda _{y}L=0$} \\ (M+2m)\dot{z} &=&\text{constant} \tag{$\Lambda _{z}L=0$} \\ \left( 2mr^{2}+\frac{1}{12}Ml^{2}\right) \dot{\varphi}\sin ^{2}\theta &=& \text{constant} \tag{$\Lambda _{\varphi }L=0$} \\ \ddot{r}-r\dot{\theta}^{2}-r\dot{\varphi}^{2}\sin ^{2}\theta +\frac{K}{m} (r-r_{0}) &=&0 \tag{$\Lambda _{r}L=0$} \\ \left( r^{2}+\frac{Ml^{2}}{24m}\right) \ddot{\theta}+2r\dot{r}\dot{\theta} -\left( r^{2}+\frac{ml^{2}}{24m}\right) \dot{\varphi}^{2}\sin \theta \cos \theta &=&0 \tag{$\Lambda _{\theta }L=0$}\end{align}\]

Las tres primeras ecuaciones muestran que los tres componentes del momento lineal del centro de masa son constantes de movimiento. La cuarta ecuación muestra que el componente del momento angular alrededor del\(z^{\prime }\) eje es una constante de movimiento. Dado que el\(z_{1}\) eje ha sido elegido arbitrariamente entonces se debe conservar el momento angular total. Las ecuaciones quinta y sexta dan las ecuaciones radiales y angulares de movimiento de las masas oscilantes\(m\).