7.2: Impulso Generalizado

Consideremos un sistema holonómico de\(N\) masas bajo la influencia de fuerzas conservadoras que dependen de la posición\(q_{j}\) pero no de la velocidad\( \dot{q}_{j}\), es decir, el potencial es independiente de la velocidad. Luego para la\( x\) coordenada de partícula\(i\) para\(N\) partículas

\[\begin{align} \frac{\partial L}{\partial \dot{x}_{i}} &= \frac{\partial T}{\partial \dot{x} _{i}}-\frac{\partial U}{\partial \dot{x}_{i}}=\frac{\partial T}{\partial \dot{x}_{i}} \label{7.1}\\[4pt] &= \frac{\partial }{\partial \dot{x}_{i}}\sum_{i=1}^{N}\frac{1}{2} m_{i}\left( \dot{x}_{i}^{2}+\dot{y}_{i}^{2}+\dot{z}_{i}^{2}\right) \notag\\[4pt] &= m_{i}\dot{x}_{i}=p_{i,x} \notag\end{align}\]

Así, para un potencial holonómico, conservador e independiente de la velocidad tenemos

\[\frac{\partial L}{\partial \dot{x}_{i}}=p_{i,x} \label{7.2}\]que es el\(x\) componente del momento lineal para la\(i^{th}\) partícula.

Este resultado sugiere una evidente extensión del concepto de impulso a coordenadas generalizadas. El impulso generalizado asociado a la coordenada\(q_{j}\) se define como

\[\frac{\partial L}{\partial \dot{q}_{j}}\equiv p_{j}\label{7.3}\]Obsérvese que\(p_{j}\) también se denomina el momento conjugado o impulso canónico a\(q_{j}\) donde\(q_{j},p_{j}\) se encuentran las variables conjugadas, o canónicas. Recuerde que el impulso lineal\(p_{j}\) es la integral de tiempo de primer orden dada por la ecuación\((2.4.1)\). Si no\(q_{j}\) es una coordenada espacial, entonces\( p_{j}\) es el impulso generalizado, no el impulso lineal cinemático. Por ejemplo, si\(q_{j}\) es un ángulo, entonces\(p_{j}\) será momento angular. Es decir, el impulso generalizado puede diferir del momento lineal o angular habitual ya que la definición\ ref {7.3} es más general que la\(p_{x}=m \dot{x}\) definición habitual de momento lineal en la mecánica clásica. Esto se ilustra por el caso de partículas cargadas en movimiento\(m_{j},e_{j}\) en un campo electromagnético. Capítulo\(6\) mostró que las fuerzas electromagnéticas sobre una carga\(e_{j}\) pueden ser descritas en términos de un potencial escalar\(U_{j}\) donde

\[U_{j}=e_{j}(\Phi -\mathbf{A\cdot v}_{j}\mathbf{)}\label{7.4}\]

Así, el Lagrangiano para la fuerza electromagnética puede escribirse como

\[L=\sum_{j=1}^{N}\left[ \frac{1}{2}m_{j}\mathbf{v}_{j}\cdot \mathbf{v} _{j}-e_{j}(\Phi -\mathbf{A\cdot v}_{j}\mathbf{)}\right]\label{7.5}\]

El impulso generalizado a la coordenada\(x_{j}\) para carga\(e_{j},\) y masa\(m_{j},\) viene dado por el lagrangiano anterior

\[p_{j,x}=\frac{\partial L}{\partial \dot{x}_{j}}=m_{j}\dot{x}_{j}+e_{j}A_{x}\label{7.6}\]

Tenga en cuenta que esto incluye tanto el momento lineal mecánico más el momento electromagnético correcto. El hecho de que el campo electromagnético lleve impulso no debería ser una sorpresa ya que las ondas electromagnéticas también transportan energía como lo ilustra la transmisión de energía radiante del sol.

Ejemplo\(\PageIndex{1}\): Feynman’s angular-momentum paradox

Feynman planteó la siguiente paradoja [Fey84]. Un disco aislante circular\(,\) montado sobre cojinetes sin fricción, tiene un anillo circular de carga total distribuido\(q\) uniformemente alrededor del perímetro del disco circular en el radio\(R\). Un solenoide superconductor largo de radio\(s\), donde\(s<R\), se fija al disco y se monta coaxial con los cojinetes. El momento de inercia del sistema alrededor del eje de rotación es\(I\). Inicialmente el disco más el solenoide superconductor son estacionarios con una corriente constante produciendo un campo magnético uniforme\(B_{0}\) dentro del solenoide. Supongamos que un aumento en la temperatura del solenoide destruye la superconductividad conduciendo a una rápida disipación de la corriente eléctrica y el campo magnético resultante. Supongamos que el sistema es libre de girar, no hay otras fuerzas o pares que actúen sobre el sistema, y que los portadores de carga en el solenoide tienen masa cero y por lo tanto no contribuyen al momento angular. ¿El sistema gira cuando se detiene la corriente en el solenoide?

Figura\(\PageIndex{1}\)

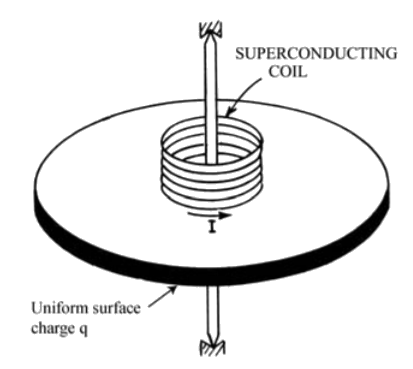
Inicialmente el sistema es estacionario con cero momento angular mecánico. La Ley de Faraday establece que, cuando el campo magnético se disipe de\(B_{0}\) a cero, habrá un par que\(\mathbf{N}\) actuará sobre la carga circunferencial\(q\) en el radio\(R\) debido al cambio en el flujo magnético\(\Phi\).

\[\mathbf{N}(t)=-qR\frac{d\Phi }{dt} \nonumber\]

Ya que\(\frac{d\Phi }{dt}<0\), este par conduce a un impulso angular que igualará el momento angular mecánico final.

\[\mathbf{L}_{final}^{MECH}=\mathbf{T=}\int_{t}\mathbf{N}(t)dt=qR\mathbf{\Phi }\nonumber\]

El momento angular inicial en el campo electromagnético se puede derivar usando la Ecuación\ ref {7.6}, más el teorema de Stoke (Apéndice\(19.8.3\)). La ecuación\(2.12.56\) da que el momento angular final es igual al impulso angular

\[\mathbf{L}_{initial}^{EM}=R\int_{t}\oint r\dot{p}_{\phi }dldt=R\oint rp_{\phi }dl=qR\oint A_{\phi }dl=qR\int \mathbf{B\cdot dS=}qR\mathbf{\Phi }\nonumber\]

donde\(\Phi =\oint A_{\phi }dl=\int \mathbf{B\cdot dS}\) está el flujo magnético total inicial a través del solenoide. Por lo tanto, el momento angular inicial total viene dado por

\[\mathbf{L}_{initial}^{TOTAL}=0+\mathbf{L}_{initial}^{EM}=qR\mathbf{\Phi }\nonumber\]

Dado que el campo electromagnético final es cero, el momento angular total final viene dado por

\[\mathbf{L}_{final}^{TOTAL}=\mathbf{L}_{final}^{MECH}+0=qR\mathbf{\Phi }\nonumber\]

Tenga en cuenta que el momento angular total se conserva. Es decir, inicialmente todo el momento angular se almacena en el campo electromagnético, mientras que el momento angular final es todo mecánico. Esto explica la paradoja de que no se conserva el momento angular mecánico, solo se conserva el momento angular total del sistema, es decir, la suma de los momentos angulares mecánicos y electromagnéticos.