7.10: Invarianza hamiltoniana

Los capítulos\(7.8,7.9\) abordaron dos características importantes e independientes del hamiltoniano con respecto a:\(a)\) cuándo\(H\) se conserva, y\(b\)) cuándo\(H\) es igual a la energía mecánica total. Estos importantes resultados se resumen a continuación con una discusión de los supuestos hechos al derivar el hamiltoniano, así como las implicaciones.

a) Conservación de la energía generalizada

El teorema de la energía generalizada\((7.8.1)\) se dio como

\[\dfrac{dH\left( \mathbf{q,p,}t\right) }{dt}=\dfrac{dh(\mathbf{q},\mathbf{\dot{q }},t)}{dt}=\sum_{j}\dot{q}_{j}\left[ Q_{j}^{EXC}+\sum_{k=1}^{m}\lambda _{k} \dfrac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)\right] -\dfrac{\partial L( \mathbf{q},\mathbf{\dot{q}},t)}{\partial t} \label{7.46}\]

Tenga en cuenta que cuando

\[\sum_{j}\dot{q}_{j}\left[ Q_{j}^{EXC}+\sum_{k=1}^{m}\lambda _{k}\dfrac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)\right] =0, \nonumber\]

entonces la Ecuación\ ref {7.46} reduce a

\[\dfrac{dH}{dt}=-\dfrac{\partial L}{\partial t}\label{7.47}\]

Además, cuando

\[\sum_{j}\dot{q}_{j}\left[ Q_{j}^{EXC}+\sum_{k=1}^{m}\lambda _{k} \dfrac{\partial g_{k}}{\partial q_{j}}(\mathbf{q},t)\right] =0, \nonumber\]

y si el lagrangiano no es una función explícita del tiempo, entonces el hamiltoniano es una constante de movimiento. Es decir, \(H\)se conserva si, y sólo si, lo lagrangiano, y consecuentemente el hamiltoniano, no son funciones explícitas del tiempo, y si las fuerzas externas son cero.

b) La energía generalizada y la energía total

Si se cumplen los dos requisitos siguientes

1. La energía cinética tiene una dependencia cuadrática homogénea de las velocidades generalizadas, es decir, la transformación a coordenadas generalizadas es independiente del tiempo, \( \dfrac{\partial x_{\alpha ,i}}{\partial t}=0.\)
2. La energía potencial no depende de la velocidad, así los términos\(\dfrac{\partial U}{\partial \dot{q}_{i}}=0.\)

Entonces la ecuación\((7.9.5)\) implica que el hamiltoniano equivale a la energía mecánica total, es decir,\[H=T+U=E\label{7.48}\]

Expresado en palabras, la energía generalizada (hamiltoniana) es igual a la energía total si las restricciones son independientes del tiempo y la energía potencial es independiente de la velocidad. Esto equivale a afirmar que, si las restricciones, o coordenadas generalizadas, para el sistema son independientes del tiempo, entonces\(H=E\).

Las cuatro combinaciones de las dos condiciones independientes anteriores, asumiendo que el término de fuerzas externas en la Ecuación\ ref {7.46} es cero, se resumen en la tabla\(\PageIndex{1}\).

Tabla\(\PageIndex{1}\): Energía hamiltoniana y total

Hamiltoniano	Restricciones y transformación de coordenadas	Restricciones y transformación de coordenadas
Comportamiento del tiempo	Independiente del tiempo	Dependiente del tiempo
\(\dfrac{dH}{dt}=-\dfrac{\partial L}{\partial t}=0\)	\(H\)conservados,\(H=E\)	\( H\)conservados,\(H\neq E\)
\(\dfrac{dH}{dt}=-\dfrac{\partial L}{\partial t}\neq 0\)	\(H\)no conservada,\( H=E\)	\(H\)no conservada,\(H\neq E\)

Obsérvese los siguientes hechos generales relativos al lagrangio y al hamiltoniano.

1. el lagrangiano es indefinido con respecto a la adición de una constante al potencial escalar,
2. el lagrangiano es indefinido con respecto a la adición de una velocidad constante,
3. no hay una elección única de coordenadas generalizadas.
4. el hamiltoniano es una función escalar que se deriva de la función escalar lagrangiana.
5. el impulso generalizado se deriva del lagrangiano.

Estos hechos, más la capacidad de reconocer las condiciones bajo las cuales\(H\) se conserva, y cuándo\(H=E,\) pueden facilitar en gran medida la solución de problemas como lo demuestran los siguientes dos ejemplos.

Ejemplo\(\PageIndex{1}\): Linear harmonix oscillator on a cart moving at constant velocity

Considera un oscilador armónico lineal ubicado en un carro que se mueve con velocidad constante\(v_{0}\) en la\(x\) dirección (Figura\(\PageIndex{1}\)). Deje que el marco de laboratorio sea el marco sin imprimar, y el marco del carro se designe como marco imprimado. Supongamos que\(x=x^{\prime }\) en\(t=0.\) Entonces

Figura\(\PageIndex{1}\): Oscilador armónico en carro moviéndose a velocidad uniforme\(v_0\).

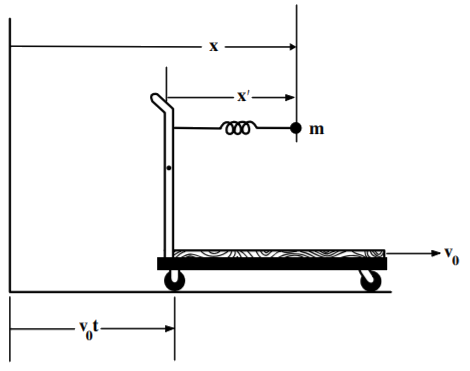
\[x^{\prime }=x-v_{0}t \hspace{0.85in}\dot{x}^{\prime }=\dot{x}-v_{0}\hspace{0.85in}\ddot{x} ^{\prime }=\ddot{x}\nonumber\]

El oscilador armónico tendrá una energía potencial de\[U=\dfrac{1}{2}kx^{\prime 2}=\dfrac{1}{2}k\left( x-v_{0}t\right) ^{2}\nonumber\]

Marco de laboratorio:

El Lagrangiano es

\[L(x,\dot{x},t)=\dfrac{m\dot{x}^{2}}{2}-\dfrac{1}{2}k\left( x-v_{0}t\right) ^{2}\nonumber\]

La ecuación de Lagrange\(\Lambda _{x}L=0\) da la ecuación de movimiento a ser

\[m\ddot{x}=-k(x-v_{0}t) \nonumber\]

La definición de impulso generalizado da

\[p=\dfrac{\partial L}{\partial \dot{x}}=m\dot{x}\nonumber\]

El hamiltoniano es

\[\begin{align*} H(x,p,t) &=\sum_{i}\dot{q}_{i}\dfrac{\partial L}{\partial \dot{q}_{i}}-L \\[4pt] &=\dfrac{ p^{2}}{2m}+\dfrac{1}{2}k\left( x-v_{0}t\right) ^{2}\end{align*}\]

El hamiltoniano es la suma de las energías cinéticas y potenciales e iguala a la energía total del sistema, pero no se conserva desde entonces\(L\) y\(H\) son ambas funciones explícitas del tiempo, es decir\(\dfrac{dH}{dt}=\dfrac{\partial H}{\partial t}=-\dfrac{\partial L}{ \partial t}\neq 0\). Físicamente esto se entiende en que la energía debe fluir dentro y fuera de la restricción externa manteniendo el carro moviéndose uniformemente a una velocidad constante\(v_{0}\) contra la reacción a la masa oscilante. Es decir, asumir una velocidad uniforme para el carro móvil constituye una restricción dependiente del tiempo en la masa, y la fuerza de restricción funciona en el desplazamiento real del sistema completo. Si la restricción no existiera, entonces el impulso del carro oscilaría de tal manera que se conserva el impulso total del sistema de carro más resorte.

Bastidor del carro:

Transformar el Lagrangiano a las coordenadas cebadas en el marco de referencia móvil, que también es un marco inercial. Entonces el lagrangiano\(L,\) en términos de las coordenadas del marco del carro móvil, es

\[L(x^{\prime },\dot{x}^{\prime },t)=\dfrac{m}{2}\left( \dot{x}^{\prime 2}+2 \dot{x}^{\prime }v_{0}+v_{0}^{2}\right) -\dfrac{1}{2}kx^{\prime 2}\nonumber\]

La ecuación de movimiento de Lagrange\(\Lambda _{x^{\prime }}L=0\) da la ecuación de movimiento a ser

\[m\ddot{x}^{\prime }=-kx^{\prime }\nonumber\]

donde\(x^{\prime }\) se encuentra el desplazamiento de la masa con respecto al carro. Esto implica que un observador en el carro observará el movimiento armónico simple como es de esperar del principio de equivalencia en la relatividad galilea.

La definición del impulso generalizado da el impulso lineal en las coordenadas del marco cebado para ser

\[p^{\prime }=\dfrac{\partial L}{\partial \dot{x}^{\prime }}=m\dot{x}^{\prime }+mv_{0}\nonumber\]

El carrito-marco Hamiltoniano también se puede expresar en términos de las coordenadas en el marco móvil para ser

\[H(x^{\prime },p^{\prime },t)=\dot{x}^{\prime }\dfrac{\partial L}{\partial \dot{x}^{\prime }}-L=\dfrac{\left( p^{\prime }-mv_{0}\right) ^{2}}{2m}+\dfrac{1 }{2}kx^{\prime 2}-\dfrac{m}{2}v_{0}^{2}\nonumber\]

Obsérvese que los lagrangianos y hamiltonianos expresados en términos de las coordenadas en el marco de referencia del carro no son explícitamente dependientes del tiempo, por lo tanto\(H\) se conserva. Sin embargo, el hamiltoniano carta-marco no equivale a la energía total ya que la transformación de coordenadas depende del tiempo. En realidad los dos primeros términos en el hamiltoniano anterior son la energía del oscilador armónico en el marco del carro. Este ejemplo muestra que los hamiltonianos difieren cuando se expresan en términos de marcos de referencia ya sea de laboratorio o carro

Ejemplo\(\PageIndex{2}\): Isotropic central force in a rotating frame

Considerar una masa sujeta a una fuerza radial isotrópica central\(U(r)\) como se muestra en la Figura\(\PageIndex{2}\). Comparar el hamiltoniano\(H\) en el marco fijo de referencia\(S\), con el hamiltoniano\(H^{\prime }\) en un marco de referencia\(S^{\prime }\) que está girando alrededor del centro de la fuerza con velocidad angular constante\( \omega\).

Figura\(\PageIndex{2}\): Masa sujeta a fuerza radial

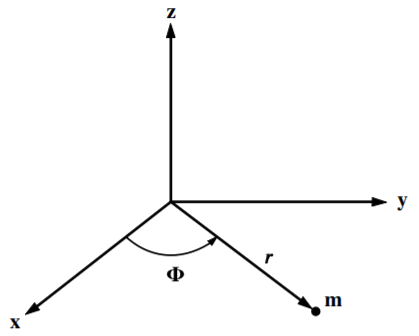
Restringir este caso a la rotación alrededor de un eje para que solo dos coordenadas polares\(r\) y\(\phi\) necesiten ser consideradas. Las transformaciones son

\[\begin{aligned} r^{\prime } &=&r \\ \phi ^{\prime } &=&\phi -\omega t\end{aligned}\]

También

\[U(r)=U(r^{\prime })\nonumber\]

Marco fijo de referencia\(S\):

\[L=T-U= \dfrac{m}{2}\left( \dot{r}^{2}+r^{2}\dot{\phi}^{2}\right) -U(r)\nonumber\]Dado que el lagrangiano no depende explícitamente del tiempo, entonces se conserva el hamiltoniano. Para este hamiltoniano de marco fijo los momentos generalizados son

\[\begin{aligned} p_{\phi } &=&\dfrac{\partial L}{\partial \dot{\phi}}=m\dot{r}^{2}\dot{\phi} \\ p_{r} &=&\dfrac{\partial L}{\partial \dot{r}}=m\dot{r}\end{aligned}\]

El hamiltoniano iguala

\[H(p_{r},p_{\phi },r,\phi )=\sum_{i}\dot{q}_{i}\dfrac{\partial L}{\partial \dot{q}_{i}}-L=\dfrac{1}{2m}\left( p_{r}^{2}+\dfrac{p_{\phi }}{r^{2}} ^{2}\right) +U(r)=E \nonumber\]

El hamiltoniano en el marco fijo se conserva y equivale a la energía total, es decir\(H=T+U\).

Marco giratorio de referencia\(S^{\prime }\)

El Lagrangiano de marco fijo inercial anterior se puede escribir en términos de las coordenadas cebadas (marco giratorio no inercial) como

\[L=T-U=\dfrac{m}{2}\left( \dot{r}^{2}+r^{2}\dot{\phi}^{2}\right) -U(r)=\dfrac{m }{2}\left( \dot{r}^{\prime 2}+r^{\prime 2}\left( \dot{\phi}^{\prime }+\omega \right) ^{2}\right) -U(r^{\prime })\nonumber\]

Los momentos generalizados derivados de este lagrangiano son

\[\begin{aligned} p_{\phi }^{\prime } &=&\dfrac{\partial L}{\partial \dot{\phi}^{\prime }}=m \dot{r}^{\prime 2}\left( \dot{\phi}^{\prime }+\omega \right) =p_{\phi ^{\prime }}^{\prime }+mr^{\prime 2}\omega \\ p_{r}^{\prime } &=&\dfrac{\partial L}{\partial \dot{r}^{\prime }}=m\dot{r} ^{\prime 2}=p_{r}\end{aligned}\]

El hamiltoniano expresado en términos de las coordenadas del marco giratorio no inercial es

\[H^{\prime }(p_{r}^{\prime },p_{\phi }^{\prime },r^{\prime },\phi ^{\prime })= \dfrac{\partial L}{\partial \dot{r}^{\prime }}\dot{r}^{\prime }+\dfrac{ \partial L}{\partial \dot{\phi}^{\prime }}\dot{\phi}^{\prime }-L=\dfrac{1}{2m} \left( p_{r}^{\prime 2}+\dfrac{\left( p_{\phi ^{\prime }}^{\prime }+mr^{2}\omega \right) }{r^{2}}\right) +U(r^{\prime })\nonumber\]

Tenga en cuenta que\(H^{\prime }(p_{r}^{\prime },p_{\phi }^{\prime },r^{\prime },\phi ^{\prime })\) es independiente del tiempo y por lo tanto se conserva, pero\(H(p_{r}^{\prime },p_{\phi }^{\prime },r^{\prime },\phi ^{\prime })\neq E\) porque las coordenadas generalizadas son dependientes del tiempo. Además,\(p_{\phi ^{\prime }}^{\prime }\) se conserva desde\[\dot{p}_{\phi }^{\prime }=\dfrac{\partial H}{\partial \phi ^{\prime }}=-\dfrac{ \partial L}{\partial \phi ^{\prime }}=0\nonumber\]

Ejemplo\(\PageIndex{3}\): The plane pendulum

El péndulo plano simple en un campo gravitacional uniforme\(g\) es un ejemplo que ilustra la invarianza hamiltoniana.

Figura\(\PageIndex{3}\): El péndulo plano restringido a oscilar en un plano vertical en un campo gravitacional uniforme.

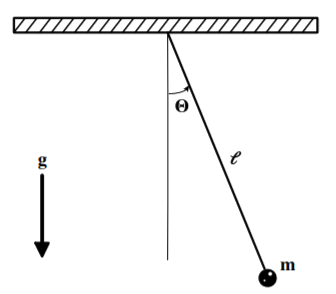
Solo hay una coordenada generalizada,\(\theta\) y la lagrangiana para este sistema es

\[L= \dfrac{1}{2}ml^{2}\dot{\theta}^{2}+mgl\cos \theta \nonumber\]

El momento conjugado a\(\theta\) es

\[p_{\theta }=\dfrac{\partial L}{\partial \dot{\theta}}=ml^{2}\dot{\theta} \nonumber\]que es el momento angular alrededor del punto de pivote.

Usando la ecuación de Lagrange-Euler esto da que

\[\dfrac{d}{dt}p_{\theta }=\dot{p}_{\theta }=\dfrac{\partial L}{\partial \theta } =-mgl\sin \theta \nonumber\]Tenga en cuenta que el momento angular no\(p_{\theta }\) es una constante de movimiento ya que depende explícitamente de\(\theta\).

El hamiltoniano es\[H=\sum_{i}p_{i}\dot{q}_{i}-L=p_{\theta }\dot{\theta}-L=\dfrac{1}{2}ml^{2}\dot{ \theta}^{2}-mgl\cos \theta =\dfrac{p_{\theta }^{2}}{2ml^{2}}-mgl\cos \theta \nonumber\]

Obsérvese que los lagrangianos y hamiltonianos no son funciones explícitas del tiempo, por lo tanto se conservan. También el potencial es independiente de la velocidad y no hay transformación de coordenadas, por lo que el hamiltoniano equivale a la energía total\(E,\) que es una constante de movimiento. \[H=\dfrac{p_{\theta }^{2}}{2ml^{2}}-mgl\cos \theta =E \nonumber\]

Ejemplo\(\PageIndex{4}\): Oscillating cylinder in a cylindrical bowl

Es importante tener en cuenta correctamente las fuerzas de restricción cuando se usa el teorema de Noether para sistemas restringidos. El teorema de Noether asume que las variables son independientes. Esto se ilustra considerando el ejemplo de un cilindro macizo rodando en una cubeta cilíndrica fija. Supongamos que un cilindro uniforme de radio\(\rho\) y masa\(m\) está limitado a rodar sin deslizarse sobre la superficie interna de la mitad inferior de un cilindro hueco de radio\(R\). El movimiento está restringido para asegurar que los ejes de ambos cilindros permanezcan paralelos y\( \rho <R\).

Figura\(\PageIndex{4}\)

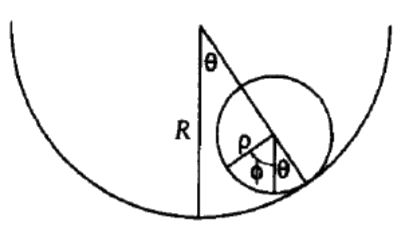
Las coordenadas generalizadas se toman como los ángulos\(\theta\) y\(\phi\) que se miden con respecto a un eje vertical fijo. Entonces la energía cinética y la energía potencial son

\[T=\dfrac{1}{2}m\left[ \left( R-\rho \right) \dot{\theta}\right] ^{2}+\dfrac{1}{ 2}I\dot{\phi}^{2}\hspace{1in}U=\left[ R-\left( R-\rho \right) \cos \theta \right] mg \nonumber\]

donde\(m\) es la masa del cilindro pequeño y donde\( U=0\) en la posición más baja de la esfera. El momento de inercia de un cilindro uniforme es\(I=\dfrac{1}{2}m\rho ^{2}\).

El Lagrangiano es

\[L-T-U=\dfrac{1}{2}m\left[ \left( R-\rho \right) \dot{\theta}\right] ^{2}+ \dfrac{1}{4}m\rho ^{2}\dot{\phi}^{2}-\left[ R-\left( R-\rho \right) \cos \theta \right] mg \nonumber\]

Dado que el cilindro sólido gira sin deslizarse dentro de la carcasa cilíndrica, entonces la ecuación de restricción es\[g(\theta \phi )=R\theta -\rho \left( \phi +\theta \right) =0 \nonumber\]

Usar el Lagrangiano, más la única ecuación de restricción, requiere un multiplicador de Lagrange. Entonces las ecuaciones de Lagrange de movimiento para\(\theta\) y\(\phi\) son

\[\begin{aligned} \dfrac{\partial L}{\partial \theta }-\dfrac{d}{dt}\left[ \dfrac{\partial L}{ \partial \dot{\theta}}\right] +\lambda \dfrac{\partial g}{\partial \theta } &=&0 \\ \dfrac{\partial L}{\partial \phi }-\dfrac{d}{dt}\left[ \dfrac{\partial L}{ \partial \dot{\phi}}\right] +\lambda \dfrac{\partial g}{\partial \phi } &=&0\end{aligned}\]

Sustituir el Lagrangiano y la ecuación de restricción da dos ecuaciones de movimiento

\[\begin{aligned} -\left( R-\rho \right) mg\sin \theta -m\left( R-\rho \right) ^{2}\ddot{\theta }+\lambda \left( R-\rho \right) &=&0 \\ -\dfrac{1}{2}m\rho ^{2}\ddot{\phi}-\lambda \rho &=&0\end{aligned}\]

La ecuación inferior de movimiento da que

\[\lambda =-\dfrac{1}{2}m\rho \ddot{\phi} \nonumber\]

Sustituir esto en la ecuación de restricción da

\[\lambda =-\dfrac{1}{2}m\left( R-\rho \right) \ddot{\theta} \nonumber\]

Sustituir esto en la primera ecuación de movimiento da la ecuación de movimiento\(\theta\) para ser

\[\ddot{\theta}=\dfrac{2g}{3\left( R-\rho \right) }\sin \theta\nonumber\]

es decir

\[\lambda =-\dfrac{mg}{3}\sin \theta\nonumber\]

El par que actúa sobre el cilindro pequeño debido a la fuerza de fricción es

\[F\rho =\dfrac{1}{2}m\rho ^{2}\ddot{\phi}=-\lambda \rho\nonumber\]

Así, la fuerza de fricción es\[F=-\lambda =\dfrac{mg}{3}\sin \theta\nonumber\]

El teorema de Noether se puede utilizar para determinar si el momento angular\( p_{\theta }\) es una constante de movimiento. El derivado del Lagrangiano

\[\dfrac{\partial L}{\partial \theta }=\left( R-\rho \right) mg\sin \theta\nonumber\]

y así lo dicen las ecuaciones de Lagrange\(\dot{p}_{\theta }=\left( R-\rho \right) mg\sin \theta\). Por lo tanto, no\(p_{\theta }\) es una constante de movimiento.

El lagrangiano no es una función explícita de la\(\phi ,\) cual sugeriría que\(p_{\phi }\) es una constante de movimiento. Pero esto es incorrecto porque la ecuación de restricción se\(\phi =\dfrac{\left( R-\rho \right) }{\rho }\theta\) acopla\(\theta\) y\( \phi\), es decir, no son variables independientes, y por lo tanto\( p_{\theta }\) y\(p_{\phi }\) están acopladas por la ecuación de restricción. Como resultado no\(p_{\phi }\) es una constante de movimiento porque está directamente acoplada a la\(p_{\theta }=\left( R-\rho \right) mg\sin \theta\) cual no es una constante de movimiento. Así,\(p_{\theta }\) ni\(p_{\phi }\) son constantes de movimiento. Esto ilustra que se deben tener en cuenta cuidadosamente las ecuaciones de restricción, y las fuerzas de restricción concomitantes, al aplicar el teorema de Noether que tácitamente asume variables independientes.

El hamiltoniano se puede derivar usando el momento generalizado

\[\begin{aligned} p_{\theta } &=&\dfrac{\partial L}{\partial \dot{\theta}}=m\left( R-\rho \right) ^{2}\dot{\theta} \\ p_{\phi } &=&\dfrac{\partial L}{\partial \dot{\phi}}=\dfrac{1}{2}m\rho ^{2} \dot{\phi}\end{aligned}\]

Entonces el hamiltoniano es dado por

\[H=p_{\theta }\dot{\theta}+p_{\phi }\dot{\phi}-L=\dfrac{p_{\theta }^{2}}{ 2m\left( R-\rho \right) ^{2}}+\dfrac{p_{\phi }^{2}}{m\rho ^{2}}+\left[ R-\left( R-\rho \right) \cos \theta \right] mg\nonumber\]

Tenga en cuenta que la transformación a coordenadas generalizadas es independiente del tiempo y el potencial no depende de la velocidad, por lo que el hamiltoniano también equivale a la energía total. También el hamiltoniano se conserva desde entonces\(\dfrac{dH}{dt}=0\).