7.E: Simetrías, Invarianza y el Hamiltoniano (Ejercicios)

1. Considera una partícula de masa\(m\) moviéndose en un plano y sujeta a una fuerza de atracción cuadrada inversa.
   1. Obtener las ecuaciones de movimiento.
   2. ¿Se conserva el momento angular sobre el origen?
   3. Obtener expresiones para las fuerzas generalizadas.
2. Considerar una función lagrangiana de la forma\(L(q_{i},\dot{q_{i}% },\ddot{q_{i}},t)\). Aquí el lagrangiano contiene una derivada temporal de las coordenadas generalizadas que es superior a la primera. Cuando se trabaja con tales lagrangianos, se emplea el término “mecánica generalizada”.
   1. Considera un sistema con un grado de libertad. Al aplicar los métodos del cálculo de las variaciones, y asumiendo que el principio de Hamilton se mantiene con respecto a las variaciones que mantienen ambas\(q\) y\(\dot{q}\) fijas en los puntos finales, muestran que la ecuación de Lagrange correspondiente es

      \[\frac{d^{2}}{dt^{2}}\left( \frac{\partial L}{\partial \ddot{q}}\right) - \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}}\right) +\frac{% \partial L}{\partial q}=0.\]

      Tales ecuaciones de movimiento tienen aplicaciones interesantes en la teoría del caos.

   2. Aplica este resultado al Lagrangiano

      \[L=-\frac{m}{2}q\ddot{q}-\frac{k}{2}q^{2}.\]

      ¿Reconoces las ecuaciones del movimiento?

3. Un cilindro sólido uniforme de radio\(R\) y masa\(M\) descansa sobre un plano horizontal y un cilindro idéntico descansa sobre él tocando a lo largo de la parte superior del primer cilindro con los ejes de ambos cilindros paralelos. Al cilindro superior se le da un desplazamiento infinitossimal para que ambos cilindros rueden sin deslizarse en las direcciones que muestran las flechas.
   1. Encuentra Lagrangian para este sistema
   2. ¿Cuáles son las constantes de movimiento?
   3. Demostrar que mientras los cilindros permanezcan en contacto entonces

      \[\dot{\theta}^{2}=\frac{12g\left( 1-\cos \theta \right) }{R\left( 17+4\cos \theta -4\cos ^{2}\theta \right) }\]

      

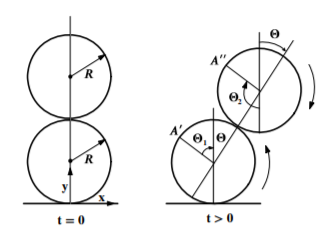
      Figura\(\PageIndex{1}\)

4. Considere una molécula diatómica que tiene un eje de simetría a lo largo de la línea a través del centro de los dos átomos que comprenden la molécula. Considera que esta molécula está rotando alrededor de un eje perpendicular al eje de simetría y que no hay fuerzas externas que actúen sobre la molécula. Utilice el Teorema de Noether para responder a las siguientes preguntas:
   1. ¿Se conserva el momento angular total?
   2. ¿Se conserva la proyección del momento angular total a lo largo de un\(z\) eje fijo al espacio?
   3. ¿Se conserva la proyección del momento angular a lo largo del eje de simetría de la molécula giratoria?
   4. ¿Se conserva la proyección del momento angular perpendicular al eje de simetría giratoria?
5. Una cuenta de masa\(m\) se desliza bajo gravedad a lo largo de un alambre liso doblado en forma de parábola\(x^{2}=az\) en el\((x,z)\) plano vertical.
   1. ¿Sobre qué tipo (holonómico, no holonómico, escleronómico, reonómico) de restricción actúa\(m\)?
   2. Configure la ecuación de movimiento de Lagrange para\(x\) con la restricción incrustada.
   3. Configure las ecuaciones de movimiento de Lagrange para ambos\(x\) y\(z\) con la restricción unida y un multiplicador lagrangiano\(% \lambda\) introducido.
   4. Mostrar que la misma ecuación de movimiento para\(x\) los resultados de cualquiera de los métodos utilizados en la parte (b) o parte (c).
   5. Expresar\(\lambda\) en términos de\(x\) y\(\dot{x}\)
   6. ¿Cuáles son los\(x\) y\(z\) componentes de la fuerza de restricción en términos de\(x\) y\(\dot{x}\)?
6. Que el plano horizontal sea el\(x-y\) plano. Un talón de masa\(m\) está limitado a deslizarse con velocidad a\(v\) lo largo de una curva descrita por la función\(y=f(x)\). ¿Qué fuerza aplica la curva a la cuenta? (Ignorar gravedad)
7. Considera la máquina Atwood que se muestra. Las masas son\(4m\),\(5m\), y\(3m\). Dejar\(x\) y\(y\) ser las alturas de las dos masas derechas con respecto a sus posiciones iniciales.
   1. Resuelve este problema usando las ecuaciones de Euler-Lagrange b) Usa el teorema de Noether para encontrar el impulso conservado.
   2. Usa el teorema de Noether para encontrar el impulso conservado.

      

      Figura\(\PageIndex{2}\)

8. Un cubo de lado\(2b\) y centro de masa\(C\), se coloca sobre un cilindro horizontal fijo de radio\(r\) y centro\(O\) como se muestra en la figura. Originalmente el cubo se coloca de tal manera que\(C\) está centrado arriba\(O\) pero puede rodar de lado a lado sin resbalar. (a) Suponiendo que\(b<r\) utilice el enfoque lagrangiano para encontrar la frecuencia para pequeñas oscilaciones alrededor de la parte superior del cilindro. Para simplificar, haga la aproximación de ángulo pequeño para\(L\) antes de usar las ecuaciones de Lagrange-Euler. b) ¿Cuál será la moción si\(b>r\)? Tenga en cuenta que el momento de inercia del cubo alrededor del centro de masa es\(\frac{2}{3}mb^{2}\).

   

   Figura\(\PageIndex{3}\)

9. Dos masas iguales de masa\(m\) se pegan a un aro sin masa de radio\(R\) es libre de girar alrededor de su centro en un plano vertical. El ángulo entre las masas es\(2\theta\), como se muestra. Encuentra la frecuencia de las oscilaciones.

   

   Figura\(\PageIndex{4}\)

10. Tres palos sin masa cada uno de longitud\(2r\), y masa\(% m\) con el centro de masa en el centro de cada palo, están articulados en sus extremos como se muestra. El extremo inferior del palo inferior está abisagrado en el suelo. Se sujetan de manera que los dos palos inferiores son verticales, y el superior se inclina en un pequeño ángulo\(\varepsilon\) con respecto a la vertical. Luego son liberados. Al instante de la liberación cuáles son las tres ecuaciones de movimiento derivadas de la lagrangiana derivada asumiendo que\(\varepsilon\) es pequeña\(?\) Úselas para determinar las aceleraciones angulares iniciales de los tres palos.

    

    Figura\(\PageIndex{5}\)