8.4: Estadísticas de Bose-Einstein y Fermi-Dirac

Por último, en esta sección derivaremos las estadísticas de Bose-Einstein y Fermi-Dirac. En particular, nos interesa el equilibrio térmico para un gran número de partículas idénticas (no interaccionantes) con algún espectro de energía\(E_{j}\), que mi ser continuo.

Como el número de partículas no es fijo, estamos tratando con el Gran Conjunto Canónico. Su función de partición\(\Xi\) viene dada por

\[\Xi=\operatorname{Tr}\left[e^{\mu \beta \hat{n}-\beta H}\right],\tag{8.43}\]

donde\(H\) está el hamiltoniano de varios cuerpos,\(\beta=1 / k_{B} T\) y\(\mu\) es el potencial químico. El número promedio de partículas con energía\(\boldsymbol{E}_{j}\) de una sola partícula viene dado entonces por

\[\left\langle n_{j}\right\rangle=-\frac{1}{\beta} \frac{\partial \ln \Xi}{\partial E_{j}}.\tag{8.44}\]

Para el simple caso donde\(H=\sum_{j} E_{j} \hat{n}_{j}\) y los operadores de creación y aniquilación obedecen al álgebra del conmutador, el exponente puede escribirse como

\[\exp \left[\beta \sum_{j}\left(\mu-E_{j}\right) \hat{a}_{j}^{\dagger} \hat{a}_{j}\right]=\bigotimes_{j} \sum_{n_{j}=0}^{\infty} e^{\beta\left(\mu-E_{j}\right) n_{j}}\left|n_{j}\right\rangle\left\langle n_{j}\right|,\tag{8.45}\]

y el rastro se convierte

\[\Xi=\prod_{j} \frac{1}{1-e^{\beta\left(\mu-E_{j}\right)}}.\tag{8.46}\]

El número promedio de fotones para la energía\(\boldsymbol{E}_{j}\) es

\[\left\langle n_{j}\right\rangle=-\frac{1}{\beta} \frac{\partial \ln \Xi}{\partial E_{j}}=-\frac{1}{\beta \Xi} \frac{\partial \Xi}{\partial E_{j}}=\frac{1}{e^{-\beta\left(\mu-E_{j}\right)}-1}.\tag{8.47}\]

Esta es la distribución de Bose-Einstein para partículas con energía\(E_{j}\). Se muestra para aumentar\(E_{j}\) en la Fig. 4 a la izquierda.

Figura 4: Izquierda: Distribución de Bose-Einstein para diferentes temperaturas\((\mu=0)\). Cuanto menor es la temperatura, más partículas ocupan los estados de baja energía. Derecha: Distribución Fermi-Dirac para diferentes temperaturas y\(\mu=1\). Los fermiones no ocuparán estados energéticos con números superiores a 1, y por lo tanto las energías superiores son necesariamente pobladas. Los valores de energía\(E_{j}\) forman un continuo en el eje horizontal.

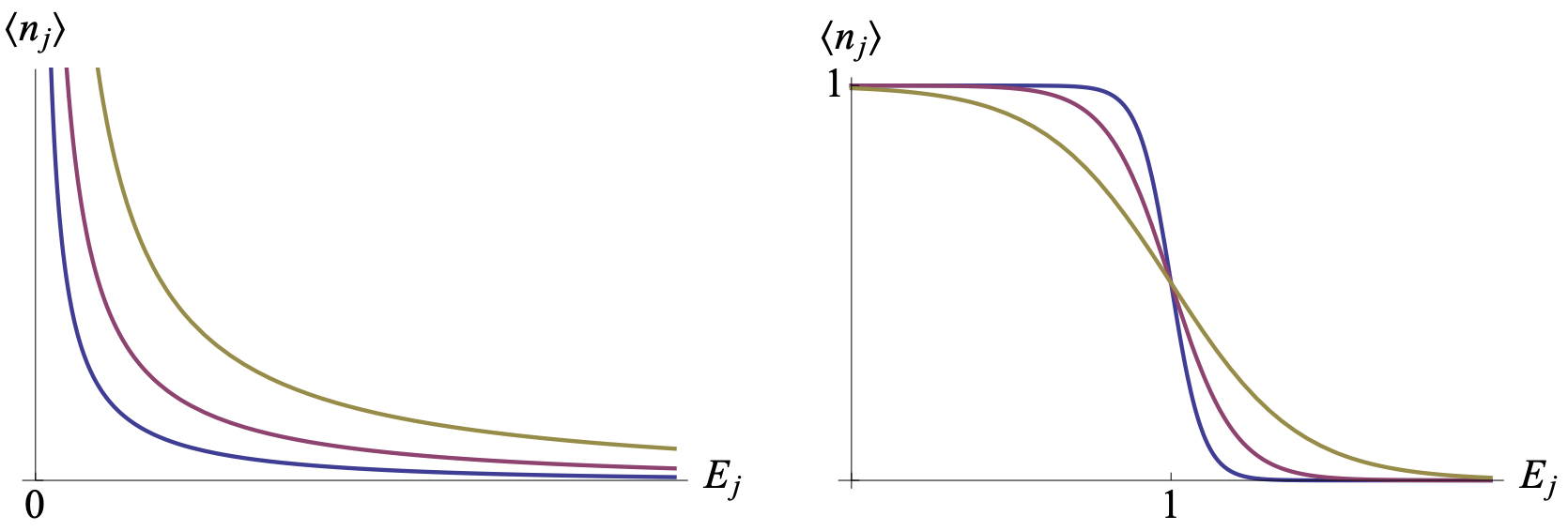
Alternativamente, si los operadores de creación y aniquilación obedecen a las relaciones anti-conmutación, la suma sobre\(n_{j}\) en la Ec. (8.45) no va de 0 a ∞, sino por encima de 0 y 1. La función de partición del gran conjunto canónico se convierte entonces

\[\Xi=\prod_{j}\left[1+e^{\beta\left(\mu-E_{j}\right)}\right],\tag{8.48}\]

y el número promedio de partículas con energía\(E_{j}\) se convierte en

\[\left\langle n_{j}\right\rangle=-\frac{1}{\beta \Xi} \frac{\partial \Xi}{\partial \hbar \omega_{j}}=\frac{1}{e^{-\beta\left(\mu-E_{j}\right)}+1}.\tag{8.49}\]

Esta es la estadística de Fermi-Dirac para estas partículas, y se muestra en la Fig. 4 a la derecha. El potencial químico es la energía ocupada más alta a temperatura cero, y en la física de estado sólido esto se llama el nivel Fermi. Anote la diferencia de signo en el denominador con respecto a las estadísticas de Bose-Einstein.

Ejercicios

1. Calcular el determinante Slater para tres electrones y mostrar que no pueden estar dos electrones en el mismo estado.
2. Estadística de partículas.
   1. ¿Cuál es la probabilidad de encontrar\(n\) bosones con energía\(E_{j}\) en estado térmico?
   2. ¿Cuál es la probabilidad de encontrar\(n\) fermiones con energía\(E_{j}\) en estado térmico?
3. Considere un sistema de bosones idénticos (que no interactúan) con un espectro de energía discreta y una energía de estado fundamental\(\boldsymbol{E}_{0}\). Además, el potencial químico comienza por debajo de la energía del estado fundamental\(\mu<E_{0}\).
   1. Calcular\(\left\langle n_{0}\right\rangle\) y aumentar el potencial químico a\(\mu \rightarrow E_{0}\) (por ejemplo, bajando la temperatura). ¿Qué pasa cuando\(\mu\) pasa\(\boldsymbol{E}_{0}\)?
   2. ¿Cuál es el comportamiento de\(\left\langle n_{\text {thermal }}\right\rangle \equiv \sum_{j=1}^{\infty}\left\langle n_{j}\right\rangle\) as\(\mu \rightarrow E_{0}\)? Bosquejo ambos\(\left\langle n_{0}\right\rangle\) y\(\left\langle n_{\text {thermal }}\right\rangle\) en función de\(\mu\). ¿Cuál es la fracción de partículas en el estado fundamental\(\mu=E_{0}\)?
   3. ¿Qué proceso físico describe esto?
4. El proceso\(U=\exp \left(r \hat{a}_{1}^{\dagger} \hat{a}_{2}^{\dagger}-r^{*} \hat{a}_{1} \hat{a}_{2}\right)\) con\(r \in \mathbb{C}\) crea partículas en dos sistemas, 1 y 2, cuando se aplican al estado de vacío\(|\Psi\rangle=U|\varnothing\rangle\).
   1. Demostrar que los operadores bosónicos\(\hat{a}_{1}^{\dagger} \hat{a}_{2}^{\dagger}\) y\(\hat{a}_{1} \hat{a}_{2}\) obedecen el álgebra

      \(\left[K_{-}, K_{+}\right]=2 K_{0} \quad \text { and } \quad\left[K_{0}, K_{\pm}\right]=\pm K_{\pm},\)

      con\(K_{+}=K_{-}^{\dagger}\).

   2. Para los operadores que obedecen el álgebra en (a) podemos escribir

      \ [\ begin {alineado}
      e^ {r K_ {+} -r^ {*} K_ {-}} =\ exp\ izquierda [\ frac {r} {|r|}\ tanh |r| K_ {+}\ derecha] &\ exp\ izquierda [-2\ ln (\ cosh |r|) K_ {0}\ derecha]\\
      &\ veces\ exp\ izquierda [-\ frac {r^ {*}} {|r|}\ tanh |r| K_ {-}\ derecho].
      \ end {alineado}\ tag {8.50}\]

      Calcular el estado\(|\Psi\rangle\) de los dos sistemas.

   3. La cantidad de enredo entre dos sistemas se puede medir por la entropía\(S(r)\) de la matriz de densidad reducida\(\rho_{1}=\operatorname{Tr}_{1}[\rho]\) para uno de los sistemas. Calcular\(S(r)=-\operatorname{Tr}\left[\rho_{1} \ln \rho_{1}\right]\).
   4. ¿Cuál es la probabilidad de encontrar\(n\) partículas en el sistema 1?