1.6: Evolución del tiempo

Para el factor dependiente del tiempo\(a_{n}(t)\),, de cada componente (57) de la solución general (69), nuestro procedimiento dio un resultado muy simple y universal (62), describiendo un cambio lineal de la fase\(\varphi_{n} \equiv\)\(\arg \left(a_{n}\right)\) de esta compleja función en el tiempo, con la tasa constante \[\frac{d \varphi_{n}}{d t}=-\omega_{n}=-\frac{E_{n}}{\hbar},\]para que las partes reales e imaginarias de\(a_{n}\) oscilen sinusoidalmente con esta frecuencia. La relación (70) coincide con la conjetura de Einstein (5), pero ¿podrían estas oscilaciones de las funciones de onda representar una realidad física? En efecto, para los fotones, descritos por la Ecuación (5),\(E\) puede ser (y como veremos en el Capítulo 9, es) la energía real y bien definida de un fotón, y\(\omega\) es la frecuencia de la radiación así cuantificada. Sin embargo, para las partículas no relativistas, descritas por la mecánica de las olas, la energía potencial\(U\), y por lo tanto la energía total\(E\), se definen a una constante arbitraria, porque podemos medirlas desde un nivel de referencia arbitrario. ¿Cómo puede ese cambio del nivel de referencia de energía (que puede hacerse solo en nuestra mente) alterar la frecuencia de oscilaciones de una variable?

Según las ecuaciones (22) - (23), esta evolución temporal de una función de onda no afecta a la distribución de probabilidad de la partícula, ni siquiera a ninguna observable (incluida la energía\(E\), siempre que se refiera siempre al mismo origen que\(U\)), en cualquier estado estacionario. Sin embargo, combinemos la ecuación (5) con la suposición de Bohr (7):\[\hbar \omega_{n n^{\prime}}=E_{n^{\prime}}-E_{n} .\] La diferencia\(\omega_{n n}\) 'de las frecuencias propias\(\omega_{n}\) y\(\omega_{n}\), participando en esta fórmula, es evidentemente independiente de la referencia energética, y como se demostrará más adelante en el curso , determina la frecuencia medible de la radiación electromagnética (o posiblemente de una onda de diferente naturaleza física) emitida o absorbida en la transición cuántica entre los estados.

Como otro ejemplo pero relacionado, considere dos partículas similares 1 y 2, cada una en el mismo estado propio (digamos, la energía más baja), pero con sus energías potenciales (y por lo tanto las energías del estado fundamental\(E_{1,2}\)) diferentes por una constante\(\Delta U \equiv U_{1}-U_{2}\). Entonces, según la Ec. (70), la diferencia\(\varphi \equiv \varphi_{1}-\varphi_{2}\) de sus fases de función de onda evoluciona en el tiempo con la tasa independiente de referencia\[\frac{d \varphi}{d t}=-\frac{\Delta U}{\hbar} .\] Ciertos instrumentos de medición, débilmente acoplados a las partículas, pueden permitir la observación de esta evolución, manteniendo la dinámica cuántica de la partícula prácticamente imperturbable, es decir, la Ec. (70) intacta. Quizás la medición más dramática de este tipo es posible usando el efecto Josephson en enlaces débiles entre dos superconductores\(-\) ver Fig. \(7.47\)

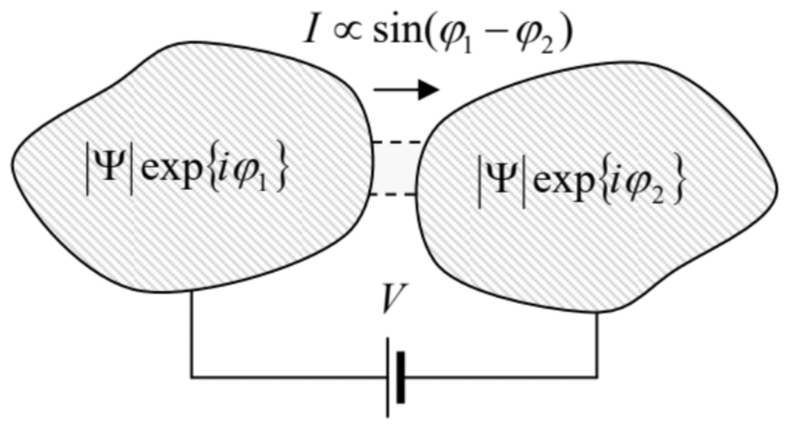Fig. 1.7. El efecto Josephson en un vínculo débil entre dos electrodos superconductores a granel.

Como breve recordatorio, la\({ }^{48}\) superconductividad puede explicarse por un acoplamiento específico entre electrones de conducción en sólidos, que conduce, a bajas temperaturas, a la formación de los llamados pares Cooper. Dichos pares, cada uno compuesto por dos electrones con espines y momentos opuestos, se comportan como partículas de Bose y forman un condensado coherente de Bose-Einstein. \({ }^{49}\)La mayoría de las propiedades de dicho condensado pueden describirse mediante una única función de onda común\(\Psi\), evolucionando en el tiempo igual que la de una partícula libre, con la energía potencial efectiva\(U=q \phi=-2 e \phi\), donde\(\phi\) está el potencial electroquímico, \({ }^{50}\)y\(q=-2 e\) es la carga eléctrica de un par Cooper. Como resultado, para el sistema mostrado en la Fig. 7, en el que el voltaje aplicado externamente\(V\) fija la diferencia\(\phi_{1}-\phi_{2}\) entre los potenciales electroquímicos de dos superconductores, la Ec. (72) toma la forma\[\frac{d \varphi}{d t}=\frac{2 e}{\hbar} V .\] Si el enlace entre los superconductores es lo suficientemente débil, el la corriente eléctrica\(I\) de los pares Cooper (llamada la supercorriente) a través del enlace puede describirse aproximadamente mediante la siguiente relación simple,\[I=I_{\mathrm{c}} \sin \varphi,\] donde\(I_{\mathrm{c}}\) hay alguna constante, dependiente de la fuerza del eslabón débil. \({ }^{51}\)Ahora combinando las ecuaciones (73) y (74), vemos que si el voltaje aplicado\(V\) es constante en el tiempo, la corriente oscila sinusoidalmente, con la llamada frecuencia Josephson\[\omega_{\mathrm{J}} \equiv \frac{2 e}{\hbar} V,\] tan alta como\(\sim 484 \mathrm{MHz}\) por microvoltios de voltaje dc aplicado. Este efecto puede ser fácilmente observado experimentalmente: aunque su detección directa es un poco complicada, es fácil observar el bloqueo de fase (sincronización)\(5^{52}\) de las oscilaciones Josephson mediante una señal de frecuencia de microondas externa\(\omega\). Tal bloqueo de fase da como resultado la relación\(\omega_{\mathrm{J}}=n \omega\) satisfecha dentro de ciertos intervalos de corriente continua y, por lo tanto, en la formación, en la\(I-V\) curva dc del enlace débil, de pasos de corriente prácticamente verticales a voltajes de CC\[V_{n}=n \frac{\hbar \omega}{2 e},\] donde\(n\) es un número entero. \({ }^{53}\)Dado que las frecuencias pueden estabilizarse y medirse con muy alta precisión, este efecto se está utilizando en estándares de alta precisión de voltaje de CC.

---

\({ }^{47}\)El efecto fue predicho en 1962 por Brian Josephson (¡entonces estudiante de posgrado!) y observado poco después de eso.

\({ }^{48}\)Para una discusión más detallada, incluyendo la derivación de la Ec. (75), véase por ejemplo EM Capítulo 6.

\({ }^{49}\)Se puede encontrar una discusión detallada de la condensación de Bose-Einstein, por ejemplo, en SM Sec. 3.4.

\({ }^{50}\)Para más información sobre esta noción véase, e.g. SM Sec. 6.3.

\({ }^{51}\)En algunos casos, la función\(I(\varphi)\) puede desviarse algo de la ecuación (74), pero estas desviaciones no afectan su\(2 \pi\) periodicidad fundamental, y de ahí las relaciones fundamentales\((75)-(76)\). (Aún no se han encontrado correcciones a ellos).

\({ }^{52}\)Para la discusión de este efecto muy general, véase, e.g., CM Sec. 5.4.

\({ }^{53}\)El tamaño de estos pasos de corriente continua se puede calcular fácilmente a partir de las ecuaciones (73) y (74). Permítanme dejar esta tarea para el ejercicio del lector.