2.2: Paquetes de Ondas de Partículas Libres

Comencemos nuestra discusión de problemas particulares con la moción libre 1D, es decir, con\(U(x, t)=0\). A partir de la Ec. (1.29), es evidente que en el caso 1D, una solución similar “fundamental” (es decir, una particular pero la más importante) de la ecuación de Schrödinger (1) es una onda sinusoidal (“monocromática”)\[\Psi_{0}(x, t)=\text { const } \times \exp \left\{i\left(k_{0} x-\omega_{0} t\right)\right\} .\] Según las ecuaciones (1.32), describe una partícula con impulso definido\(^{2} p_{0}=\hbar k_{0}\) y energía\(E_{0}=\hbar \omega_{0}\)\(=\hbar^{2} k_{0}^{2} / 2 m\). Sin embargo, para esta función de onda, el producto\(\Psi^{*} \Psi\) no depende de ninguna\(x\) o\(t\), de manera que la partícula esté completamente deslocalizada, es decir, la probabilidad de encontrarla igual a lo largo de todos los ejes\(x\), en todo momento.

Para describir un estado localizado en el espacio, formemos, en el momento inicial del tiempo\((t=0)\), un paquete de ondas del tipo mostrado en la figura 1.6, multiplicando la forma de onda sinusoidal (15) por alguna función envolvente suave\(A(x)\). Como el ejemplo particular más importante, considere el paquete de onda gaussiana\[\Psi(x, 0)=A(x) e^{i k_{0} x}, \quad \text { with } A(x)=\frac{1}{(2 \pi)^{1 / 4}(\delta x)^{1 / 2}} \exp \left\{-\frac{x^{2}}{(2 \delta x)^{2}}\right\}\] (Por cierto, la Fig. 1.6a muestra exactamente un paquete de este tipo). El factor preexponencial en esta función envolvente ha sido seleccionado en la forma de tener la densidad de probabilidad inicial,\[w(x, 0) \equiv \Psi^{*}(x, 0) \Psi(x, 0)=A^{*}(x) A(x)=\frac{1}{(2 \pi)^{1 / 2} \delta x} \exp \left\{-\frac{x^{2}}{2(\delta x)^{2}}\right\}\] normalizada como en la Ec. (3), para cualquier parámetro\(\delta x\) y\(k_{0} \cdot{ }^{3}\)

Para explorar la evolución de este paquete de ondas en el tiempo, podríamos intentar resolver la Ecuación (1) con la condición inicial (16) directamente, pero en el espíritu de la discusión en la Sec. 1.5, es más fácil proceder de manera diferente. Primero representemos la función de onda inicial (16) como una suma (1.67) de las funciones propias de la ecuación\(\psi_{k}(x)\) de Schrödinger 1D estacionaria correspondiente (1.60), en nuestro caso actual\[-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{k}}{d x^{2}}=E_{k} \psi_{k}, \quad \text { with } E_{k} \equiv \frac{\hbar^{2} k^{2}}{2 m},\] que son simplemente ondas monocromáticas,\[\psi_{k}=a_{k} e^{i k x} .\] Since (como se discutió en la Sec. 1.7) en el movimiento sin restricciones el espectro de posibles números de onda\(k\) es continuo, la suma (1.67) debe ser reemplazada por una integral: 4\[\Psi(x, 0)=\int a_{k} e^{i k x} d k\] Ahora notemos que desde el punto de vista de las matemáticas, la Ec. (20) es solo la transformada de Fourier habitual a partir de la variable\(k\) a la variable “conjugada”\(x\), y podemos usar la conocida fórmula de la transformada recíproca de Fourier para escribir\[a_{k}=\frac{1}{2 \pi} \int \Psi(x, 0) e^{-i k x} d x=\frac{1}{2 \pi} \frac{1}{(2 \pi)^{1 / 4}(\delta x)^{1 / 2}} \int \exp \left\{-\frac{x^{2}}{(2 \delta x)^{2}}-i \widetilde{k} x\right\} d x, \quad \text { where } \widetilde{k} \equiv k-k_{0} .\] Esta integral gaussiana puede elaborarse mediante el siguiente método estándar, que se utilizará muchas veces en este curso. Complementemos el exponente al cuadrado completo de una combinación lineal de\(x\) y\(k\), sumando un término compensador independiente de\(x\):\[-\frac{x^{2}}{(2 \delta x)^{2}}-i \widetilde{k} x \equiv-\frac{1}{(2 \delta x)^{2}}\left[x+2 i(\delta x)^{2} \widetilde{k}\right]^{2}-\widetilde{k}^{2}(\delta x)^{2} .\] Dado que la integración en el lado derecho de la Ec. (21) debe realizarse en constante \(\widetilde{k}\), en los infinitos límites de\(x\), su resultado no cambiaría si reemplazamos\(d x\) por\(d x^{\prime} \equiv d\left[x+2 i(\delta x)^{2} \widetilde{k}\right]\). Como resultado, obtenemos: 5\[\begin{aligned} a_{k} &=\frac{1}{2 \pi} \frac{1}{(2 \pi)^{1 / 4}(\delta x)^{1 / 2}} \exp \left\{-\widetilde{k}^{2}(\delta x)^{2}\right\} \int \exp \left\{-\frac{x^{\prime 2}}{(2 \delta x)^{2}}\right\} d x^{\prime} \\ &=\left(\frac{1}{2 \pi}\right)^{1 / 2} \frac{1}{(2 \pi)^{1 / 4}(\delta k)^{1 / 2}} \exp \left\{-\frac{\widetilde{k}^{2}}{(2 \delta k)^{2}}\right\} \end{aligned}\] así que\(a_{k}\) también tiene una distribución gaussiana, ahora a lo largo del\(k\) eje -, centrada al valor\(k_{0}\) (Fig. 1.6b), con la constante\(\delta k\) definida como\[\delta k \equiv 1 / 2 \delta x .\] Así podemos representar la inicial paquete de onda (16) como\[\Psi(x, 0)=\left(\frac{1}{2 \pi}\right)^{1 / 2} \frac{1}{(2 \pi)^{1 / 4}(\delta k)^{1 / 2}} \int \exp \left\{-\frac{\left(k-k_{0}\right)^{2}}{(2 \delta k)^{2}}\right\} e^{i k x} d k .\] A partir de la comparación de esta fórmula con la Ec. (16), es evidente que la incertidumbre r.m.s. del número de onda\(k\) en este paquete es efectivamente igual a la\(\delta k\) definida por la Ec. (24), justificando así la notación. La comparación de la última relación con la Ec. (1.35) muestra que el paquete gaussiano representa el último caso en el que el producto\(\delta x \delta p=\delta x(\hbar \delta)\) tiene el menor valor posible\((\hbar / 2)\); para cualquier otra forma de sobre, el producto de incertidumbre solo puede ser mayor. Por supuesto, podríamos obtener el mismo resultado\(\delta k\) de la ecuación (16) usando las definiciones (1.23), (1.33) y (1.34); la ventaja real de la ecuación (25) es que se puede generalizar fácilmente a\(t>0\). En efecto, ya sabemos que la evolución temporal de la función de onda siempre viene dada por la Ec. (1.69), para nuestro caso actual\(^{6}\)\[\Psi(x, t)=\left(\frac{1}{2 \pi}\right)^{1 / 2} \frac{1}{(2 \pi)^{1 / 4}(\delta k)^{1 / 2}} \int \exp \left\{-\frac{\left(k-k_{0}\right)^{2}}{(2 \delta k)^{2}}\right\} e^{i k x} \exp \left\{-i \frac{\hbar k^{2}}{2 m} t\right\} d k\]

La Fig. 1 muestra varias instantáneas de la parte real de la función de onda (26), para un caso particular\(\delta k=0.1 k_{0}\).

Fig. 2.1. Evolución temporal típica de un paquete de onda 1D en (a) escalas de tiempo más pequeñas y (b) mayores. Las líneas discontinuas muestran los sobres de paquetes, es decir\(\pm|\Psi|\).

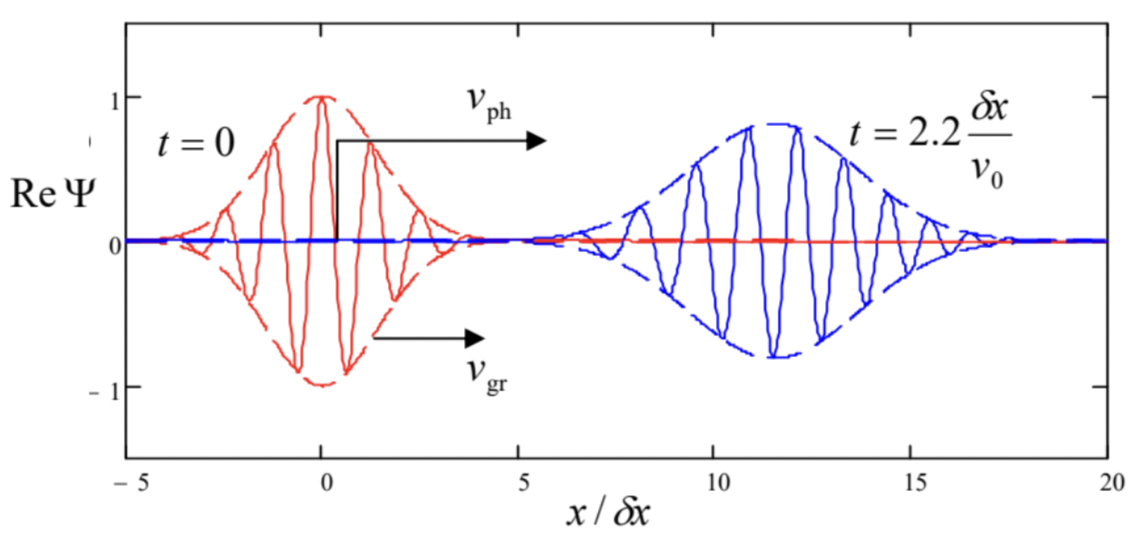
Las gráficas muestran claramente los siguientes efectos:

i) el paquete de ondas en su conjunto (caracterizado por su envolvente) se mueve a lo largo del\(x\) eje con cierta velocidad de grupo\(v_{\mathrm{gr}}\),

(ii) la onda cuasi-sinusoidal “portadora” dentro del paquete se mueve con una velocidad de fase diferente\(v_{\mathrm{ph}}\), que puede definirse como la velocidad de los puntos espaciales donde la fase de la onda\(\varphi(x, t) \equiv \arg \Psi\) toma un cierto valor fijo (digamos\(\varphi=\pi / 2\), donde \(\operatorname{Re} \Psi\)desaparece), y

(iii) el ancho espacial del paquete de ondas aumenta gradualmente con el tiempo, el paquete se propaga.

Todos estos efectos son comunes para olas de cualquier naturaleza física. \({ }^{7}\)En efecto, consideremos un paquete de\(1 \mathrm{D}\) onda del tipo (26), pero más general:\[\Psi(x, t)=\int a_{k} e^{i(k x-\omega t)} d k,\] propagarse en un medio con un arbitrario (¡pero suave!) relación de dispersión\(\omega(k)\), y asumir que la distribución del número de onda\(a_{k}\) es estrecha:\(\delta k<\left\langle\langle k\rangle \equiv k_{0}-\right.\) ver Fig. 1.6b. Entonces podemos expandir la función\(\omega(k)\) a la serie Taylor cerca del número de onda central\(k_{0}\), y mantener solo tres de sus términos principales:\[\omega(k) \approx \omega_{0}+\frac{d \omega}{d k} \widetilde{k}+\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} \widetilde{k}^{2}, \quad \text { where } \widetilde{k} \equiv k-k_{0}, \omega_{0} \equiv \omega\left(k_{0}\right),\] donde ambas derivadas tienen que ser evaluadas en el punto\(k=k_{0}\). En esta aproximación,\({ }^{8}\) la expresión entre paréntesis en el lado derecho de la Ec. (27) puede reescribirse de\[\begin{aligned} k x-\omega(k) t & \approx k_{0} x+\widetilde{k} x-\left(\omega_{0}+\frac{d \omega}{d k} \widetilde{k}+\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} \widetilde{k}^{2}\right) t \\ & \equiv\left(k_{0} x-\omega_{0} t\right)+\widetilde{k}\left(x-\frac{d \omega}{d k} t\right)-\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} \widetilde{k}^{2} t \end{aligned}\] manera que la ecuación (27) se convierta en\[\Psi(x, t) \approx e^{i\left(k_{0} x-\omega_{0} t\right)} \int a_{k} \exp \left\{i\left[\tilde{k}\left(x-\frac{d \omega}{d k} t\right)-\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} \widetilde{k}^{2} t\right]\right\} d \widetilde{k}\] Primero, descuidemos el último término entre corchetes (que es mucho menor que el primer término si la relación de dispersión es suficientemente suave y/o el intervalo de tiempo\(t\) es suficientemente pequeño), y comparar el resultado con la forma inicial del paquete de ondas (27):\[\Psi(x, 0)=\int a_{k} e^{i k x} d k=A(x) e^{i k_{0} x}, \quad \text { with } A(x) \equiv \int a_{k} e^{i \widetilde{k} x} d \widetilde{k}\] La comparación muestra que en esta aproximación, la Ec. (30) se reduce a\[\Psi(x, t)=A\left(x-v_{\mathrm{gr}} t\right) e^{i k_{0}\left(x-v_{\mathrm{ph}} t\right)},\] donde\(v_{\mathrm{gr}}\) y \(v_{\mathrm{ph}}\)son dos constantes con la dimensión de velocidad:\[\left.v_{\mathrm{gr}} \equiv \frac{d \omega}{d k}\right|_{k=k_{0}},\left.\quad v_{\mathrm{ph}} \equiv \frac{\omega}{k}\right|_{k=k_{0}}\] Claramente, la Ec. (32) describe los efectos (i) y (ii) enumerados anteriormente. Para el caso particular de las ondas de Broglie, cuya ley de dispersión viene dada por la Ec. (1.30),\[\left.v_{\mathrm{gr}} \equiv \frac{d \omega}{d k}\right|_{k=k_{0}}=\frac{\hbar k_{0}}{m} \equiv v_{0},\left.\quad v_{\mathrm{ph}} \equiv \frac{\omega}{k}\right|_{k=k_{0}}=\frac{\hbar k_{0}}{2 m}=\frac{v_{\mathrm{gr}}}{2} .\] Vemos que (muy afortunadamente :-) la velocidad de la envolvente del paquete de ondas es igual a\(v_{0}\) - la velocidad clásica de la misma partícula.

A continuación, el último término entre corchetes de la ecuación (30) describe el efecto (iii), la propagación del paquete de ondas. Se puede evaluar fácilmente si el paquete (27) es inicialmente gaussiano, como en nuestro ejemplo (25):\[a_{k}=\text { const } \times \exp \left\{-\frac{\widetilde{k}^{2}}{(2 \delta k)^{2}}\right\} \text {. }\] En este caso la integral (30) es gaussiana, y puede elaborarse exactamente como la integral (21), es decir, representando los exponentes fusionados bajo la integral como un cuadrado completo de una combinación lineal de \(x\)y\(k\):\[\begin{aligned} &-\frac{\widetilde{k}^{2}}{(2 \delta k)^{2}}+i \widetilde{k}\left(x-v_{\mathrm{gr}} t\right)-\frac{i}{2} \frac{d^{2} \omega}{d k^{2}} \widetilde{k}^{2} t \\ &\equiv-\Delta(t)\left(\widetilde{k}+i \frac{x-v_{\mathrm{gr}} t}{2 \Delta(t)}\right)^{2}-\frac{\left(x-v_{\mathrm{gr}} t\right)^{2}}{4 \Delta(t)}+i k_{0} x-\frac{i}{2} \frac{d^{2} \omega}{d k^{2}} k_{0}^{2} t, \end{aligned}\] donde he introducido la siguiente función compleja del tiempo:\[\Delta(t) \equiv \frac{1}{4(\delta k)^{2}}+\frac{i}{2} \frac{d^{2} \omega}{d k^{2}} t=(\delta x)^{2}+\frac{i}{2} \frac{d^{2} \omega}{d k^{2}} t\] y utilicé la Ec. (24). Ahora integrando sobre\(\widetilde{k}\), obtenemos\[\Psi(x, t) \propto \exp \left\{-\frac{\left(x-v_{\mathrm{gr}} t\right)^{2}}{4 \Delta(t)}+i\left(k_{0} x-\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} k_{0}^{2} t\right)\right\} .\] La parte imaginaria de la relación\(1 / \Delta(t)\) en este exponente da solo una contribución adicional a la fase de la onda y no afecta la distribución de probabilidad resultante\[w(x, t)=\Psi^{*} \Psi \propto \exp \left\{-\frac{\left(x-v_{\mathrm{gr}} t\right)^{2}}{2} \operatorname{Re} \frac{1}{\Delta(t)}\right\} .\] Esta es nuevamente una distribución gaussiana sobre eje\(x\), centrado a punto\(\langle x\rangle=v_{\text {gr }} t\), con la anchura r.m.s.\[\left(\delta x^{\prime}\right)^{2} \equiv\left\{\operatorname{Re}\left[\frac{1}{\Delta(t)}\right]\right\}^{-1}=(\delta x)^{2}+\left(\frac{1}{2} \frac{d^{2} \omega}{d k^{2}} t\right)^{2} \frac{1}{(\delta x)^{2}} .\] En el caso particular de las ondas de Broglie,\(d^{2} \omega / d k^{2}=\hbar / m\), de manera que\[\left(\delta x^{\prime}\right)^{2}=(\delta x)^{2}+\left(\frac{\hbar t}{2 m}\right)^{2} \frac{1}{(\delta x)^{2}} .\] La física de la dispersión de paquetes es muy sencilla: si\(d^{2} \omega / d k^{2} \neq 0\), la velocidad del grupo \(d \omega / d k\)de cada pequeño grupo\(d k\) de los componentes monocromáticos de la onda es diferente, resultando en la acumulación gradual (eventualmente, lineal) de las diferencias de las distancias recorridas por los grupos. La característica más curiosa de la ecuación (39) es que el ancho del paquete en\(t>0\) depende de su ancho\(\delta x^{\prime}(0)=\delta x\) inicial de una manera no monótona, tendiendo al infinito en ambos\(\delta x \rightarrow 0\) y\(\delta x \rightarrow \infty\). Debido a eso, para un intervalo de tiempo dado\(t\), hay un valor óptimo de\(\delta x\) que minimiza\(\delta x\) ':\[\left(\delta x^{\prime}\right)_{\min }=\sqrt{2}(\delta x)_{o p t}=\left(\frac{\hbar t}{m}\right)^{1 / 2} .\] Esta expresión puede ser utilizada para estimaciones del efecto de propagación. Debido a la pequeñez de la constante de Planck\(\hbar\) en la escala humana de las cosas, para los cuerpos macroscópicos este efecto es extremadamente pequeño incluso para intervalos de tiempo muy largos; sin embargo, para las partículas de luz puede ser muy notable: para un electrón\(\left(m=m_{\mathrm{e}} \approx\right.\)\(10^{-30} \mathrm{~kg}\)) , y\(t=1 \mathrm{~s}\), Eq. (40) rendimientos\(\left(\delta x^{\prime}\right)_{\min } \sim 1 \mathrm{~cm}\).

Obsérvese también que para cualquiera\(t \neq 0\), el paquete de ondas conserva su envolvente gaussiana, pero la última relación (24) no se satisface,\(\delta x^{\prime} \delta p>\hbar / 2\) - debido a un desplazamiento de fase gradualmente acumulado entre las ondas monocromáticas componentes. El último comentario sobre este tema: ¡en la mecánica cuántica, la propagación de paquetes de ondas no es un efecto ubicuo! Por ejemplo, en el Capítulo 5 veremos que en un oscilador cuántico, el ancho espacial de un paquete gaussiano (para ese sistema, llamado estado Glauber del oscilador) no crece monótonamente sino que se mantiene constante u oscila en el tiempo.

Ahora vamos a discutir brevemente el caso cuando el paquete de onda inicial no es gaussiano sino que se describe mediante una función de onda inicial arbitraria. Para que el próximo resultado sea más agradable estéticamente, es beneficioso generalizar nuestros cálculos a un tiempo inicial arbitrario\(t_{0}\); es evidente que si\(U\) no depende del tiempo explícitamente, es suficiente reemplazar\(t\) con \(\left(t-t_{0}\right)\)en todas las fórmulas anteriores. Con este reemplazo, la Ec. (27) se convierte\[\Psi(x, t)=\int a_{k} e^{i\left[k x-\omega\left(t-t_{0}\right)\right]} d k\] y la transformada recíproca (21) lee\[a_{k}=\frac{1}{2 \pi} \int \Psi\left(x, t_{0}\right) e^{-i k x} d x .\] Si queremos expresar estas dos fórmulas con una relación, es decir, enchufar la Eq. (42) en la Eq. (41), deberíamos darle\(x\) algún otro nombre a la variable de integración, e.g\(x_{0}\).,. (Dicha notación es apropiada porque esta variable describe el argumento de coordenadas en el paquete de onda inicial). El resultado es\[\Psi(x, t)=\frac{1}{2 \pi} \int d k \int d x_{0} \Psi\left(x_{0}, t_{0}\right) e^{i\left[k\left(x-x_{0}\right)-\omega\left(t-t_{0}\right)\right]} .\] Cambiando el orden de integración, esta expresión puede ser reescrita en la siguiente forma general:\[\Psi(x, t)=\int G\left(x, t ; x_{0}, t_{0}\right) \Psi\left(x_{0}, t_{0}\right) d x_{0},\] donde la función\(G\), generalmente llamada kernel en matemáticas, en mecánica cuántica se llama propagador. \({ }^{9}\)Su sentido físico puede entenderse considerando la siguiente condición inicial especial:\({ }^{10}\)\[\Psi\left(x_{0}, t_{0}\right)=\delta\left(x_{0}-x^{\prime}\right),\] donde\(x\) 'es un cierto punto dentro del dominio del movimiento de la partícula. En este caso particular, la Ec. (44) da\[\Psi(x, t)=G\left(x, t ; x^{\prime}, t_{0}\right) .\] Por lo tanto, el propagador, considerado como una función de sus argumentos\(x\) y\(t\) solo, es solo la función de onda de la partícula, en las condiciones iniciales\(\delta\) -funcionales (45). Así, así como la ecuación (41) puede entenderse como una expresión matemática del principio de superposición lineal en el dominio espacial de impulso (es decir, recíproco), la ecuación (44) es una expresión de este principio en el dominio espacial directo: la “respuesta” del sistema\(\Psi(x, t)\) a una condición inicial arbitraria \(\Psi\left(x_{0}, t_{0}\right)\)es solo una suma de sus respuestas a sus “rebanadas” espaciales elementales de esta función inicial, con el propagador\(G\left(x, t ; x_{0}, t_{0}\right)\) representando el peso de cada porción en la suma final.

Según las ecuaciones (43) y (44), en el caso particular de una partícula libre el propagador es igual a\[G\left(x, t ; x_{0}, t_{0}\right)=\frac{1}{2 \pi} \int e^{i\left[k\left(x-x_{0}\right)-\omega\left(t-t_{0}\right)\right]} d k,\] Calcular esta integral, hay que recordar que aquí no\(\omega\) es una constante sino una función de\(k\), dada por la relación de dispersión para las ondas parciales. En particular, para las ondas de Broglie, con\(\hbar \omega=\hbar^{2} k^{2} / 2 m\),\[G\left(x, t ; x_{0}, t_{0}\right) \equiv \frac{1}{2 \pi} \int \exp \left\{i\left[k\left(x-x_{0}\right)-\frac{\hbar k^{2}}{2 m}\left(t-t_{0}\right)\right]\right\} d k \text {. }\] Esta es una integral gaussiana nuevamente, y puede calcularse fácilmente apenas se hizo (dos veces) arriba, completando el exponente al cuadrado completo. El resultado es\[G\left(x, t ; x_{0}, t_{0}\right)=\left(\frac{m}{2 \pi i \hbar\left(t-t_{0}\right)}\right)^{1 / 2} \exp \left\{-\frac{m\left(x-x_{0}\right)^{2}}{2 i \hbar\left(t-t_{0}\right)}\right\} .\] Tenga en cuenta las siguientes características de esta compleja función (trazada en la Fig. 2):

(i) Depende sólo de las diferencias\(\left(x-x_{0}\right)\) y\(\left(t-t_{0}\right)\). Esto es natural porque el problema de propagación de partículas libres es invariante en la traducción tanto en el espacio como en el tiempo.

(ii) La forma de la función no depende de sus argumentos - simplemente reescalan la misma función: su instantánea (Fig. 2), si se traza como una función de no normalizado\(x\), simplemente se vuelve más amplia y más baja con el tiempo. Es curioso que las escalas de ampliación espacial\(\left(t-t_{0}\right)^{1 / 2}-\) así como en la difusión clásica, como resultado de una profunda analogía matemática entre la mecánica cuántica y la estadística clásica - para ser discutida más a fondo en el Capítulo\(7 .\)

(iii) De acuerdo con la relación de incertidumbre, el paquete de onda finalmente comprimido (45) tiene un ancho infinito de distribución de momento, y las colas cuasisinusoidales del propagador de partículas libres, claramente visibles en la Fig. 2, son los resultados de la propagación libre del más rápido (impulso más alto) componentes de esa distribución, en ambas direcciones desde el centro de paquetes.

Fig. 2.2. Las partes real (línea continua) e imaginaria (línea punteada) del propagador de partículas libres 1D (49).

En las siguientes secciones, me centraré principalmente en las funciones de onda monocromáticas (que, para el movimiento no confinado, pueden interpretarse como paquetes de ondas de un ancho espacial muy grande\(\delta x\)), y solo en raras ocasiones se discuten los paquetes de ondas. Mi mejor excusa es el principio de superposición lineal, es decir, nuestra capacidad conceptual para restaurar la solución general a partir de la de ondas monocromáticas de todas las energías posibles. No obstante, el lector no debe olvidar que, como lo ha ilustrado la discusión anterior, matemáticamente tal restauración no siempre es trivial.

---

\({ }^{2}\)A partir de este punto hasta el final de este capítulo, bajaré el índice\(x\) en los\(x\) -componentes de los vectores\(\mathbf{k}\) y\(\mathbf{p}\).

\({ }^{3}\)Este hecho puede probarse fácilmente usando la conocida integral de la función gaussiana (17), en límites infinitos ver, por ejemplo, MA Eq. (6.9b). También es sencillo usar MA Eq. (6.9c) para demostrar que para el paquete de onda (16), el parámetro\(\delta x\) es efectivamente la incertidumbre r.m.s. (1.34) de la coordenada\(x\), justificando así su notación.

\({ }^{4}\)Por la brevedad de la notación, a partir de este punto los signos de límite infinito se dejarán caer en todas las integrales 1D.

\({ }^{5}\)El hecho de que el cambio del argumento sea imaginario no es importante. En efecto, dado que la función bajo la integral tiende a cero en Re\(x^{\prime} \equiv \operatorname{Re} x \rightarrow \pm \infty\), la diferencia entre integrales infinitas de esta función a lo largo de ejes de\(x\) y\(x^{\prime}\) es igual a su integral de contorno alrededor del área rectangular\(x \leq \operatorname{Im} z \leq x\) '. Dado que la función también es analítica, obedece al teorema de Cauchy MA Eq. (15.1), que dice que esta integral de contorno es igual a cero.

\({ }^{6}\)Tenga en cuenta que la Ec. (26) difiere de la Ec. (16) solo por un exponente de un número puramente imaginario, y por lo tanto esta función de onda también se normaliza adecuadamente a 1 - ver Ec. (3). De ahí que la introducción del paquete de ondas ofrezca una solución natural al problema de la normalización de la onda viajera de Broglie, la cual fue mencionada en la Sec. 1.2.

\({ }^{7}\)Véase, por ejemplo, breves discusiones en CM Sec. \(6.3\)y EM Sec. \(7.2\).

\({ }^{8}\)Por cierto, en el caso particular de las ondas de Broglie descritas por la relación de dispersión (1.30), la ecuación (28) es exacta, porque\(\omega=E / \hbar\) es una función cuadrática de\(k=p / \hbar\), y todas las derivadas superiores de\(\omega\) más\(k\) desaparecer para cualquier\(k_{0}\).

\({ }^{9}\)Su notación estándar por letra\(G\) deriva del hecho de que el propagador es esencialmente la función espacio-temporal del Green, definida de manera muy similar a las funciones de Green de otras ecuaciones diferenciales ordinarias y parciales que describen diversos sistemas de física - véase, ej., CM Sec. \(5.1\)y/o EM Sec. \(2.7\)y 7.3.

\({ }^{10}\)Nótese que dicha condición inicial no es matemáticamente equivalente a una densidad de probabilidad inicial\(\delta\) -funcional (3).