2.3: Reflexión de partículas y tunelización

Ahora, pasemos a los casos en que una partícula 1D se mueve en varios perfiles potenciales\(U(x)\) que son constantes en el tiempo. Conceptualmente, el más simple de tales perfiles es un paso potencial - ver Fig. \(3 .\)

Fig. 2.3. Movimiento 1D clásico en un perfil potencial\(U(x)\).

Como estoy seguro el lector sabe, en la mecánica clásica la energía cinética de la partícula\(p^{2} / 2 m\) no puede ser negativa, por lo que si la partícula incide en tal escalón (en la Fig. 3, desde la izquierda), solo puede viajar por la región clásicamente accesible, donde su energía (conservada) completa,\[E=\frac{p^{2}}{2 m}+U(x),\] está mayor que el valor local\(U(x)\). Deje que la velocidad inicial\(v=p / m\) sea positiva, es decir, dirigida hacia el paso. Antes de que haya alcanzado el punto de inflexión clásico\(x_{\mathrm{c}}\), definido por\[U\left(x_{\mathrm{c}}\right)=E\] la igualdad, la energía cinética de la partícula\(p^{2} / 2 m\) es positiva, de manera que continúa moviéndose en la dirección inicial. Por otro lado, una partícula clásica no puede penetrar esa región clásicamente prohibida\(x>x_{\mathrm{c}}\), porque ahí su energía cinética sería negativa. De ahí que cuando la partícula alcanza el punto\(x=x_{\mathrm{c}}\), su velocidad tiene que cambiar su signo, es decir, la partícula se refleja de nuevo desde el punto de inflexión clásico.

Para ver qué dice la mecánica de olas sobre esta situación, partimos del paso potencial más simple y agudo que se muestra con la línea negra negrita en la Fig. 4:\[U(x)=U_{0} \theta(x) \equiv \begin{cases}0, & \text { at } x<0, \\ U_{0}, & \text { at } 0<x .\end{cases}\] Para esta elección, y cualquier energía dentro del intervalo\(0<E<U_{0}\), el punto de inflexión clásico es\(x_{\mathrm{c}}=0\).

Fig. 2.4. El reflejo de una onda monocromática a partir de un escalón potencial\(U_{0}>E\). (La forma de esta función de onda particular es para\(U_{0}=5 E\).) La función de onda se grafica con el mismo desfase vertical esquemático por\(E\) que los de la Fig. 1.8.

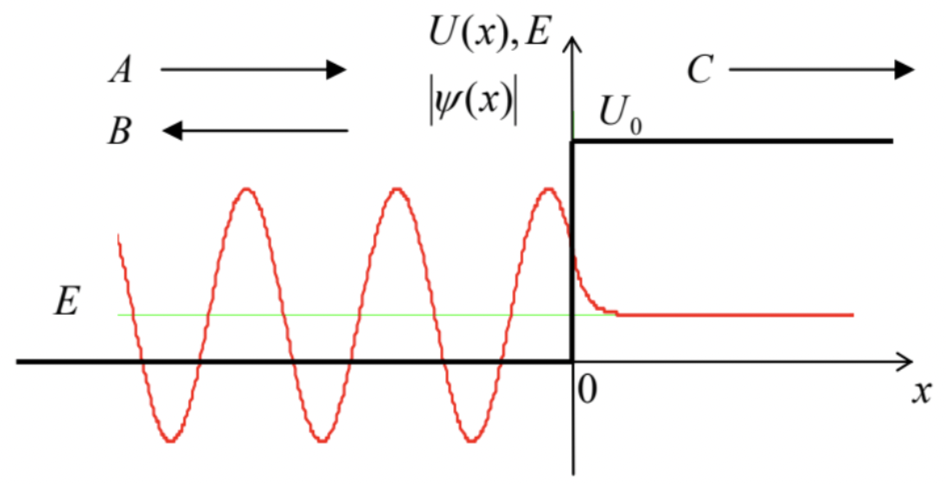
Representemos una partícula incidente con un paquete de ondas tan largo que la dispersión\(\delta k \sim 1 / \delta x\) de su espectro onda-número sea lo suficientemente pequeña como para hacer que la incertidumbre energética sea\(\delta E=\hbar \delta \omega=\hbar(d \omega / d k) \delta k\) insignificante en comparación con su valor promedio\(E<U_{0}\), así como con \(\left(U_{0}-E\right)\). En este caso,\(E\) puede considerarse como una constante dada, la dependencia temporal de la función ondaviene dada por la Eq. (1.62), y podemos calcular su factor espacial\(\psi(x)\) a partir de la versión 1D de la ecuación estacionaria de Schrödinger\((1.65): 11\)\[-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+U(x) \psi=E \psi .\] At \(x<0\), es decir\(U=0\), at, la ecuación se reduce a la ecuación de Helmholtz (1.78), y puede satisfacerse con cualquiera de las dos ondas viajeras, proporcionales a\(\exp \{+i k x\}\) y\(\exp \{-i k x\}\) correspondientemente, con\(k\) satisfacer la ecuación de dispersión (1.30):\[k^{2} \equiv \frac{2 m E}{\hbar^{2}} .\] Así, la solución general de la Ec. (53) en esta región puede representarse como\[\psi_{-}(x)=A e^{+i k x}+B e^{-i k x}\] El segundo término en el lado derecho de la ecuación (55) evidentemente describe un paquete de ondas (formalmente, infinitamente largo) que viaja hacia la izquierda, surgiendo debido a la reflexión de la partícula de el paso potencial. Si\(B=-A\), esta solución se reduce a la ecuación (1.84) para el pozo potencial con paredes infinitamente altas, pero para nuestro caso actual de una altura de escalón finito\(U_{0}\), la relación entre los coeficientes\(B\) y\(A\) puede ser diferente.

Para mostrar esto, resolvamos la Eq. (53) para\(x>0\), donde\(U=U_{0}>E\). En esta región la ecuación puede ser reescrita como\[\frac{d^{2} \psi_{+}}{d x^{2}}=\kappa^{2} \psi_{+},\] donde\(\kappa\) es una constante real y positiva definida por una fórmula similar en estructura a la Ec. (54):\[\kappa^{2} \equiv \frac{2 m\left(U_{0}-E\right)}{\hbar^{2}}>0 .\] La solución general de la Ec. (56) es la suma de\(\exp \{+\kappa x\}\) y\(\exp \{-\kappa x\}\), con arbitrario coeficientes. Sin embargo, en nuestro caso particular la función de onda debe ser finita a\(x \rightarrow+\infty\), por lo que solo el último exponente prohibido es aceptable:\[\psi_{+}(x)=C e^{-\kappa x} .\] Tal penetración de la función de onda a la región clásicamente prohibida, y por lo tanto una probabilidad distinta de cero para encontrar allí la partícula, es una de las predicciones más fascinantes de la mecánica cuántica, y se ha observado repetidamente en experimentos - por ejemplo, a través de experimentos de tunelización - ver la siguiente sección. \({ }^{12}\)A partir de la Ec. (58), es evidente que la constante\(\kappa\), definida por las ecuaciones (57), puede interpretarse como la profundidad de penetración recíproca. Incluso para las partículas más ligeras, esta profundidad suele ser muy pequeña. En efecto, para\(E<<U_{0}\) esa relación\[\left.\delta \equiv \frac{1}{\kappa}\right|_{E \rightarrow 0}=\frac{\hbar}{\left(2 m U_{0}\right)^{1 / 2}} .\] rinde Por ejemplo, consideremos un electrón de conducción en un metal típico, que corre, en la superficie del metal, en un escalón de potencial agudo cuya altura es igual a la función de trabajo del metal\(U_{0} \approx 5 \mathrm{eV}\) - ver la discusión de la efecto fotoeléctrico en la Sec. 1.1. En este caso, de acuerdo con la Ec. (59),\(\delta\) está cerca de\(0.1 \mathrm{~nm}\), es decir, está cerca de un tamaño típico de un átomo. Para partículas elementales más pesadas (e.g., protones) la profundidad de penetración es correspondientemente menor, y para cuerpos macroscópicos, apenas es medible.

Volviendo a las ecuaciones (55) y (58), aún debemos relacionar los coeficientes\(B\) y\(C\) con la amplitud\(A\) de la onda incidente, utilizando las condiciones límite en\(x=0\). Dado que\(E\) es una constante finita, y\(U(x)\) es una función finita, la Eq. (53) dice que también\(d^{2} \psi / d x^{2}\) debería ser finita. Esto significa que la primera derivada debe ser continua:\[\lim _{\varepsilon \rightarrow 0}\left(\left.\frac{d \psi}{d x}\right|_{x=+\varepsilon}-\left.\frac{d \psi}{d x}\right|_{x=-\varepsilon}\right)=\lim _{\varepsilon \rightarrow 0} \int_{-\varepsilon}^{+\varepsilon} \frac{d^{2} \psi}{d x^{2}} d x=\frac{2 m}{\hbar^{2}} \lim _{\varepsilon \rightarrow 0} \int_{-\varepsilon}^{+\varepsilon}[U(x)-E] \psi d x=0\] Repitiendo dicho cálculo para la función de onda\(\psi(x)\) misma, vemos que también debe ser continua en todos los puntos, incluido el punto fronterizo\(x=0\), para que las condiciones límite en nuestro problema sean

\[\psi_{-}(0)=\psi_{+}(0), \quad \frac{d \psi_{-}}{d x}(0)=\frac{d \psi_{+}}{d x}(0)\]Conectando las ecuaciones (55) y (58) en las ecuaciones (61), obtenemos un sistema de dos ecuaciones lineales\[A+B=C, \quad i k A-i k B=-\kappa C,\] cuya solución (fácil :-) nos permite expresar\(B\) y\(C\) vía\(A\): Inmediatamente\[B=A \frac{k-i \kappa}{k+i \kappa}, \quad C=A \frac{2 k}{k+i \kappa} .\] vemos que el numerador y denominador en la primera de estas fracciones tienen iguales módulos, así que eso\(|B|=|A|\). Esto quiere decir que, como podríamos esperar, una partícula con energía\(E<U_{0}\) se refleja totalmente desde el paso al\(-\) igual que en la mecánica clásica. Como resultado, a\(x<0\) nuestra solución (55) puede representarse como una onda estacionaria\[\psi_{-}=2 i A e^{i \theta} \sin (k x-\theta), \quad \text { with } \theta \equiv \tan ^{-1} \frac{k}{\kappa} .\] Tenga en cuenta que el desplazamiento\(\Delta x \equiv \theta / k=\left(\tan ^{-1} k / \kappa\right) / k\) de la onda estacionaria hacia la derecha, debido a la penetración parcial de la función de onda bajo el escalón potencial, es proporcional, pero generalmente no es igual a la profundidad de penetración\(\delta \equiv 1 / \kappa\). La línea roja de la Fig. 4 muestra el comportamiento exacto de la función de onda, para un caso particular\(E=U_{0} / 5\), en el que\(k / \kappa \equiv\left[E /\left(U_{0}-E\right)\right]^{1 / 2}=1 / 2\).

De acuerdo con la Ec. (59), a medida que aumenta la energía\(E\) de la partícula para aproximarse\(U_{0}\), la profundidad de penetración\(1 / \kappa\) diverge. Esto plantea un tema importante: ¿qué sucede en\(E>U_{0}\), es decir, si no hay una región clásicamente prohibida en el problema? En la mecánica clásica, la partícula incidente continuaría moviéndose hacia la derecha, aunque con una velocidad reducida, correspondiente a la nueva energía cinética\(E-U_{0}\), por lo que no habría reflexión. En mecánica cuántica, sin embargo, la situación es diferente. Para analizarlo, no es necesario volver a resolver todo el problema; basta con señalar que todos nuestros cálculos, y de ahí las ecuaciones (63) siguen vigentes si tomamos\({ }^{13}\)\[\kappa=-i k^{\prime}, \quad \text { with } \quad k^{\prime 2} \equiv \frac{2 m\left(E-U_{0}\right)}{\hbar^{2}}>0 .\] Con este reemplazo, la Eq. (63) se convierte en\({ }^{14}\)\[B=A \frac{k-k^{\prime}}{k+k^{\prime}}, \quad C=A \frac{2 k}{k+k^{\prime}} .\] El resultado más importante de este cambio es que ahora la reflexión de la partícula no es total:\(|B|<\)\(|A|\). Para evaluar este efecto cuantitativamente, es más justo usar no\(C / A\) las proporciones\(B / A\) o, sino más bien la de las corrientes de probabilidad (5) transportadas por las ondas de Broglie que viajan hacia la derecha, con amplitudes\(C\) y\(A\), en el regiones correspondientes (respectivamente, para\(x>0\) y\(x<0\)):\[\mathscr{T} \equiv \frac{I_{C}}{I_{A}}=\frac{k^{\prime}|C|^{2}}{k|A|^{2}}=\frac{4 k k^{\prime}}{\left(k+k^{\prime}\right)^{2}} \equiv \frac{4\left[E\left(E-U_{0}\right)\right]^{1 / 2}}{\left[E^{1 / 2}+\left(E-U_{0}\right)^{1 / 2}\right]^{2}}\] (El parámetro\(\mathscr{T}\) así definido se llama transparencia del sistema, en nuestro caso actual del escalón potencial de altura\(U_{0}\), a la energía de la partícula \(E\).) El resultado dado por la Ec. (67) se representa en la Fig. 5a en función de la\(U_{0} / E\) relación. Tenga en cuenta sus características más importantes:

(i) En\(U_{0}=0\), la transparencia es plena,\(\mathscr{T}=1\) -naturalmente, porque no hay ningún paso en absoluto.

(ii) At\(U_{0} \rightarrow E\), la transparencia cae a cero, dando una conexión adecuada con el caso\(E<U_{0}\).

(iii) Nada en el procedimiento de nuestra solución nos impide usar la Eq. (67) incluso para\(U_{0}<0\), es decir, para el perfil potencial reductor (o “acantilado”) - ver Fig. 5b. Muy contra-intuitivamente, la partícula se refleja (en parte) incluso desde tal acantilado, y la transmisión disminuye (aunque bastante lentamente) en\(U_{0} \rightarrow-\infty\).

Fig. 2.5. (a) La transparencia de un escalón potencial con\(U_{0}\)\(<E\) en función de su altura, de acuerdo con la Ec. (75), y (b) el perfil potencial “acantilado”, con\(U_{0}<0\).

La conclusión conceptual más importante de este análisis es que la partícula cuántica se refleja parcialmente a partir de un paso potencial con\(U_{0}<E\), en el sentido de que existe una probabilidad distinta de cero\(\mathscr{T}<1\) para encontrarla pasada sobre el escalón, mientras que también hay alguna probabilidad, \((1-\mathscr{A}>0\), para que se refleje.

Se exhibe la última propiedad, pero para cualquier relación entre\(E\) y\(U_{0}\), por otro simple perfil potencial\(U(x)\), la famosa barrera potencial (o “túnel”). La Fig. 6 muestra su versión simple, “rectangular”:\[U(x)=\left\{\begin{aligned} 0, & \text { for } x<-d / 2, \\ U_{0}, & \text { for }-d / 2<x<+d / 2, \\ 0, & \text { for }+d / 2<x . \end{aligned}\right.\] Para analizar este problema, basta con buscar la solución a la ecuación de Schrödinger en la forma (55) at\(x \leq-d / 2\). En\(x>+d / 2\), es decir, detrás de la barrera, podemos usar los argumentos presentados anteriormente (¡no hay fuente de onda a la derecha!) para mantener solo una ola viajera, ahora con el mismo número de onda:\[\psi_{+}(x)=F e^{i k x} .\] Sin embargo, bajo la barrera, es decir\(-d / 2 \leq x \leq+d / 2\), en general deberíamos mantener ambos términos exponenciales,\[\psi_{b}(x)=C e^{-\kappa x}+D e^{+\kappa x},\] porque nuestro argumento anterior, utilizado en la solución del problema de paso potencial, ya no es válido. (Aquí\(k\) y todavía\(\kappa\) están definidos, respectivamente, por las ecuaciones (54) y (57).) Para expresar los coeficientes\(B, C, D\), y a\(F\) través de la amplitud\(A\) de la onda incidente, necesitamos tapar estas soluciones en las condiciones límite similares a las ecuaciones (61), pero ahora en dos puntos límite,\(x=\pm d / 2\).

Fig. 2.6. Una barrera de potencial rectangular, y las ondas de Broglie tomadas en cuenta en su análisis.

Resolviendo el sistema resultante de 4 ecuaciones lineales, obtenemos cuatro ratios\(B / A, C / A\), etc.; en particular,\[\frac{F}{A}=\left[\cosh \kappa d+\frac{i}{2}\left(\frac{\kappa}{k}-\frac{k}{\kappa}\right) \sinh \kappa d\right]^{-1} e^{-i k d},\] y de ahí la transparencia de la barrera

\[\ \text{Rectangular tunnel barrier’s transparency}\quad\quad\quad\quad\mathscr{T} \equiv\left|\frac{F}{A}\right|^{2}=\left[\cosh ^{2} \kappa d+\left(\frac{\kappa^{2}-k^{2}}{2 \kappa k}\right)^{2} \sinh ^{2} \kappa d\right]^{-1}.\]

Entonces, la mecánica cuántica efectivamente permite que las partículas con energías\(\ E<U_{0}\) pasen “a través” de la barrera potencial — ver nuevamente la Fig. 6. Este es el famoso efecto de la tunelización mecánica cuántica. La Fig. 7a muestra la transparencia de barrera en función de la energía de las partículas\(\ E\), para varios valores característicos de su espesor\(\ d\), o más bien de la relación\(\ d / \delta\), con\(\ \delta\) definida por la Ec. (59).

Fig. 2.7. La transparencia de una barrera de potencial rectangular en función de la energía de la partícula\(E\).

Las gráficas muestran que, en general, la transparencia crece gradualmente con la energía de la partícula. Este crecimiento es natural porque la constante de penetración\(\kappa\) disminuye con el crecimiento de\(E\), es decir, la función ondulada penetra cada vez más en la barrera, de manera que cada vez más de ella se “recoge” en la segunda interfaz\((x=+d / 2)\) y se transfiere a la ola que\(F \exp \{i k x\}\) se propaga detrás de la barrera.

Ahora consideremos el límite importante de una barrera rectangular muy delgada y alta,\(d<<\delta, E<<\)\(U_{0}\), dando\(k<<\kappa<<1 / d\). En este límite, la Ec. (71) rinde\[\mathscr{T} \equiv\left|\frac{F}{A}\right|^{2} \rightarrow \frac{1}{|1+i \alpha|^{2}}=\frac{1}{1+\alpha^{2}}, \quad \text { where } \alpha \equiv \frac{1}{2}\left(\frac{\kappa^{2}-k^{2}}{\kappa k}\right) \kappa d \approx \frac{1}{2} \frac{\kappa^{2} d}{k} \approx \frac{m}{\hbar^{2} k} U_{0} d,\] El último producto\(U_{0} d\),, es solo el “área de energía” (o el “peso”)\[w \equiv \int_{U(x)>E} U(x) d x\] de la barrera. Este hecho implica que el resultado muy simple (72) puede ser correcto para una barrera de cualquier forma, siempre que sea suficientemente delgada y alta.

Para confirmar esta suposición, consideremos el problema de tunelización para una barrera muy delgada con\(\kappa d, k d\)\(<<1\), aproximándola con la\(\delta\) función de Dirac (Fig. 8):\[U(x)=w \delta(x),\] para que el parámetro\(w\) satisfaga la Ec. (73).

Fig. 2.8. Una barrera de potencial delta-funcional.

Las soluciones del problema de tunelización en todos los puntos pero\(x=0\) aún pueden tomarse en forma de ecuaciones (55) y (69), por lo que solo necesitamos analizar las condiciones de contorno en ese punto. Sin embargo, debido al carácter especial de la\(\delta\) función -, debemos tener cuidado aquí. En efecto, en lugar de la Ec. (60) ahora obtenemos\[\begin{aligned} \lim _{\varepsilon \rightarrow 0}\left(\left.\frac{d \psi}{d x}\right|_{x=+\varepsilon}-\left.\frac{d \psi}{d x}\right|_{x=-\varepsilon}\right) &=\lim _{\varepsilon \rightarrow 0} \int_{-\varepsilon}^{+\varepsilon} \frac{d^{2} \psi}{d x^{2}} d x=\lim _{\varepsilon \rightarrow 0} \frac{2 m}{\hbar^{2}} \int_{-\varepsilon}^{+\varepsilon}[U(x)-E] \psi d x \\ &=\frac{2 m}{\hbar^{2}} w_{\psi}(0) . \end{aligned}\] Según esta relación, a una finita\(w\), las derivadas también\(d \psi / d x\) son finitas, de modo que la función de onda en sí misma sigue siendo continua:\[\lim _{\varepsilon \rightarrow 0}\left(\left.\psi\right|_{x=+\varepsilon}-\left.\psi\right|_{x=+\varepsilon}\right)=\lim _{\varepsilon \rightarrow 0} \int_{-\varepsilon}^{+\varepsilon} \frac{d \psi}{d x} d x=0\] Usando estas dos condiciones de límite, obtenemos fácilmente el siguiente sistema de dos ecuaciones lineales,\[A+B=F, \quad i k F-(i k A-i k B)=\frac{2 m w}{\hbar^{2}} F,\] cuya solución rinde\[\frac{B}{A}=\frac{-i \alpha}{1+i \alpha}, \quad \frac{F}{A}=\frac{1}{1+i \alpha}, \quad \text { where } \alpha \equiv \frac{m w}{\hbar^{2} k} .\] (Tomando en cuenta la Ec. (73), esta definición de\(\alpha\) coincide con la de la Ec. (72).) Para la transparencia de la barrera\(\mathscr{T} \equiv|F / A|^{2}\), este resultado vuelve a dar el primero de los Eqs. (72), lo que por lo tanto es general para barreras tan delgadas. Esa fórmula puede ser refundido para dar la siguiente expresión simple (válida sólo para\(E<<\)\(U_{\max }\):\[\mathcal{T}=\frac{1}{1+\alpha^{2}} \equiv \frac{E}{E+E_{0}}, \quad \text { where } E_{0} \equiv \frac{m W^{2}}{2 \hbar^{2}},\] lo que demuestra que a medida que la energía se hace mayor que la constante\(E_{0}\), la transparencia se acerca a 1.

Ahora procediendo a otro límite importante de barreras gruesas\((d>>\delta)\), la Eq. (71) muestra que en este caso, la transparencia está dominada por lo que se llama el exponente del túnel:\[\mathscr{T}=\left(\frac{4 k \kappa}{k^{2}+\kappa^{2}}\right)^{2} e^{-2 \kappa d}\]

• el comportamiento que puede verse claramente como los segmentos de línea recta en las gráficas semi-logarítmicas (Fig. 7b) o\(\mathscr{T}\) como una función de la combinación\(\left(1-E / U_{0}\right)^{1 / 2}\), que es proporcional para\(\kappa-\) ver la Ec. (57). Esta dependencia exponencial del espesor de la barrera es el factor más importante para diversas aplicaciones de tunelización cuántica mecánica, desde la emisión de campo de electrones hasta el vacío\({ }^{15}\) hasta la microscopía de túnel de barrido. \({ }^{16}\)Obsérvese también implicaciones negativas muy sustanciales del efecto para el progreso de la tecnología electrónica, lo que es más importante imponer límites a la llamada escala Dennard de transistores de efecto de campo en circuitos integrados de semiconductores (que es la base tecnológica de la conocida Ley de Moore), debido al incremento de la tunelización tanto a través del óxido de puerta como a lo largo del canal de los transistores, de fuente a drenaje. \({ }^{17}\)

Finalmente, una característica más visible en la Fig. 7a (por el caso\(d=3 \delta\)) son las oscilaciones de la transparencia en función de la energía, en\(E>U_{0}\), con\(\mathcal{T}=1\), es decir, la reflexión completamente desapareciendo, en algunos puntos. \({ }^{18}\)Este es nuestro primer vistazo a un efecto cuántico más interesante: el túnel resonante. Este efecto se discutirá con más detalle en la Sec. 5 a continuación, utilizando otro perfil potencial donde se pronuncia más claramente.

---

\({ }^{11}\)Tenga en cuenta que este no es el problema propio como el que hemos resuelto en la Sec. \(1.4\)para un pozo potencial. En efecto, ahora la energía\(E\) se considera dada -por ejemplo, por las condiciones iniciales que lanzan un paquete de onda larga sobre el paso potencial- en la Fig. 4, desde la izquierda.

\({ }^{12}\)Tenga en cuenta que este efecto es pertinente a ondas de cualquier tipo, incluidas las ondas mecánicas (ver, por ejemplo, CM Secs. \(6.4\)y 7.7) y ondas electromagnéticas (ver, e.g., EM Secs. 7.3-7.7).

\({ }^{13}\)Nuestro descarte anterior de la solución particular\(\left.\exp \{x\}\right\}\), convirtiéndose ahora\(\exp \left\{-i k^{\prime} x\right\}\), sigue siendo válido, pero ahora por diferentes motivos: este término describiría un incidente de paquete de onda en el paso potencial desde la derecha, y este no es el problema bajo nuestro actual consideración.

\({ }^{14}\)Estas fórmulas son completamente similares a las que describen la reflexión parcial de las ondas clásicas desde una interfaz aguda entre dos medios uniformes, con incidencia normal (ver, por ejemplo, CM Sec. \(6.4\)y EM Sec. 7.4), siendo la impedancia efectiva\(Z\) de las ondas de Broglie proporcional a su número de ondas\(k\).

\({ }^{15}\)Véase, por ejemplo, G. Fursey, Field Emission in Vacuum Microelectronics, Kluwer, Nueva York,\(2005 .\)

\({ }^{16}\)Véase, por ejemplo, G. Binning y H. Rohrer, Helv. Phys. Acta\(\mathbf{5 5}, 726\) (1982).

\({ }^{17}\)Véase, por ejemplo, V. Sverdlov et al., IEEE Trans. on Electron Devices 50, 1926 (2003), y sus referencias. (Una breve discusión sobre los transistores de efecto campo, y literatura para su posterior lectura, se puede encontrar en SM Sec. 6.4.)

\({ }^{18}\)Permítanme mencionar de pasada el curioso caso del pozo potencial\(U(x)=-\left(\hbar^{2} / 2 m\right) \varkappa(v+1) / \cosh ^{2}(x / a)\), con cualquier entero positivo\(v\) y cualquier real\(a\), que está libre de reflejos\((\mathscr{T}=1)\) para el incidente de Broigle onda de cualquier energía \(E\), y por lo tanto para cualquier paquete de onda incidente. Desafortunadamente, una prueba de este hecho requeriría más tiempo/espacio del que puedo permitirme. (Nótese que fue descrito por primera vez en un artículo de 1930 de Paul Sophs Epstein, antes de la publicación de 1933 de G. Pöschl y E. Teller, que es responsable del nombre común de este potencial de Pöschl-Teller.)