2.4: Problemas de ejercicio

2.1. El paquete de onda inicial de una partícula 1D libre se describe mediante la Ec. (20):\[\Psi(x, 0)=\int a_{k} e^{i k x} d k .\] (i) Obtener una expresión compacta para el valor\(\langle p\rangle\) de expectativa del momento de la partícula en un momento arbitrario\(t>0\).

(ii) Calcular\(\langle p\rangle\) para el caso en que la función\(\left|a_{k}\right|^{2}\) sea simétrica con respecto a algún valor\(k_{0}\).

2.2. Calcular la función\(a_{k}\) definida por la Ec. (20), para el paquete de ondas con una envolvente espacial rectangular:\[\Psi(x, 0)= \begin{cases}C \exp \left\{i k_{0} x\right\}, & \text { for }-a / 2 \leq x \leq+a / 2, \\ 0, & \text { otherwise } .\end{cases}\] Analiza el resultado en el límite\(k_{0} a \rightarrow \infty\).

2.3. Probar la Ec. (49) para el propagador 1D de una partícula cuántica libre, a partir de la Ec. (48).

2.4. Expresar el\(1 \mathrm{D}\) propagador definido por la Ec. (44), a través de las funciones propias y energías propias de una partícula que se mueve en un potencial estacionario arbitrario\(U(x)\).

2.5. Calcular el cambio de la función de onda de una\(1 \mathrm{D}\) partícula, resultante de un pulso corto de una fuerza clásica externa que puede ser aproximada por la función delta:\({ }^{97}\)\[F(t)=P \delta(t) \text {. }\] 2.6. Calcular la transparencia\(\mathscr{T}\) de la barrera de potencial rectangular (68),\[U(x)= \begin{cases}0, & \text { for } x<-d / 2 \\ U_{0}, & \text { for }-d / 2<x<+d / 2 \\ 0, & \text { for } d / 2<x,\end{cases}\] para una partícula de energía\(E>U_{0}\). Analizar e interpretar el resultado, tomando en cuenta que\(U_{0}\) puede ser positivo o negativo. (En este último caso, estamos hablando del paso de la partícula sobre un pozo de potencial rectangular de profundidad finita)\(\left|U_{0}\right|\).

2.7. Probar la Eq. (117) para el caso\(\mathcal{T}_{\mathrm{WKB}}<<1\), utilizando las fórmulas de conexión (105).

2.8. Deletrear las funciones de onda estacionarias de un oscilador armónico en la aproximación WKB y usarlas para calcular los valores de expectativa\(\left\langle x^{2}\right\rangle\) y\(\left\langle x^{4}\right\rangle\) para el número de estado propio\(\left.n\right\rangle>1 .\)

2.9. Utilice la aproximación WKB para expresar el valor de expectativa de la energía cinética de una partícula 1D confinada en un pozo de potencial blando, en su estado\(n^{\text {th }}\) estacionario, a través de la derivada\(d E_{n} / d n\), para\(n>>1\).

2.10. Utilice la aproximación WKB para calcular la transparencia\(\mathscr{T}\) de la siguiente barrera potencial triangular:\[U(x)=\left\{\begin{array}{cc} 0, & \text { for } x<0 \\ U_{0}-F x, & \text { for } x>0 \end{array}\right.\] con\(F, U_{0}>0\), en función de la energía de la partícula incidente\(E\).

Pista: Tenga cuidado con el fuerte paso potencial en\(x=0\).

2.11. Demostrar que la simetría de la matriz de dispersión 1D S que describe un dispersor arbitrario independiente del tiempo, permite su representación en la forma (127).

2.12. Demostrar las relaciones universales entre elementos de la matriz de transferencia 1D\(\mathrm{T}\) de un dispersor estacionario (pero por lo demás arbitrario), mencionado en la Sec. \(5 .\)

2.13. Una partícula 1D había sido localizada en un pozo de potencial muy estrecho y profundo, con el “área de energía”\(\int \overline{U(x)} d x\) igual a\(-w\), donde\(w>0\). Entonces (digamos, en\(t=0\)) el fondo del pozo se levanta repentinamente, de manera que la partícula se vuelve completamente libre. Calcular la densidad de probabilidad\(w(k)\),, para encontrar la partícula en un estado con un cierto número de onda\(k\) en\(t>0\), y la energía final total del sistema.

2.14. Calcular la vida útil del estado localizado metaestable de una\(1 \mathrm{D}\) partícula en el potencial\[U(x)=-w \delta(x)-F x, \quad \text { with } w>0,\] usando la aproximación WKB. Formular la condición de validez del resultado.

2.15. Calcular los niveles de energía y las funciones propias correspondientes de una partícula 1D colocada en un pozo de potencial de fondo plano de ancho\(2 a\), con paredes duras infinitamente altas, y una barrera de potencial transparente y corta en el medio; vea la figura a la derecha. Discutir la dinámica de partículas en el límite cuando\(w\) es muy grande pero aún finita.

2.16. \({ }^{*}\)Consideremos un sistema simétrico de dos pozos potenciales del tipo mostrado en la Fig. 21, pero con\(U(0)=U(\pm \infty)=0-\) ver la figura a la derecha. Cuál es el signo de la fuerza de interacción del pozo debido a que comparten una partícula cuántica de masa\(m\), para los casos en que la partícula está en:

(i) un autoestado localizado simétrico:\(\psi_{\mathrm{S}}(-x)=\psi_{\mathrm{s}}(x)\)?

ii) un eigenstate localizado antisimétrico:\(\psi_{\mathrm{A}}(-x)=-\psi_{\mathrm{A}}(x)\)?

Utilice un enfoque alternativo para verificar su resultado para el caso particular de pozos delta-funcionales.

2.17. Derivar y analizar la ecuación característica para autoestados localizados de una partícula 1D en un pozo de potencial rectangular de profundidad finita (ver la figura de la derecha):\[U(x)=\left\{\begin{aligned} -U_{0}, & \text { for }|x| \leq a / 2, \\ 0, & \text { otherwise } \end{aligned}\right.\]

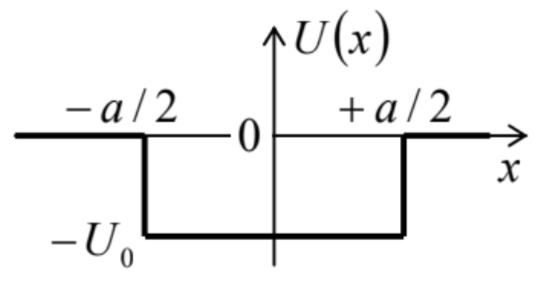
En particular, calcular el número de estados localizados en función del ancho del pozo\(a\), y explorar el límite\(U_{0}<<\hbar^{2} / 2 m a^{2}\). 2.18. Calcular la energía de una\(1 \mathrm{D}\) partícula localizada en un pozo potencial de forma arbitraria\(U(x)\), siempre que su ancho\(a\) sea finito, y la profundidad promedio sea muy pequeña:\[|\bar{U}|<<\frac{\hbar^{2}}{2 m a^{2}}, \quad \text { where } \bar{U} \equiv \frac{1}{a} \int_{\text {well }} U(x) d x\] 2.19. Una partícula de masa\(m\) se mueve en un campo con el siguiente potencial:\[U(x)=U_{0}(x)+w \delta(x) \text {, }\] donde\(U_{0}(x)\) es una función suave, simétrica con\(U_{0}(0)=0\), creciendo monótonamente en\(x \rightarrow \pm \infty\).

(i) Usar la aproximación WKB para derivar la ecuación característica para el espectro de energía de la partícula, y

(ii) describir semicuantitativamente la evolución del espectro al incremento de\(|W|\), para ambos signos de este parámetro.

Hacer que ambos resultados sean más específicos para el potencial parabólico cuadrático-parabólico (111):\(U_{0}(x)=m \omega_{0}^{2} x^{2} / 2\).

\(\underline{2.20}\). Probar la Ec. (189), a partir de la Ec. (188).

2.21. Para el problema discutido al inicio de la Sec. 7, es decir, el movimiento de la partícula 1D en un potencial infinito de peine Dirac mostrado en la Fig. 24,\[U(x)=w \sum_{j=-\infty}^{+\infty} \delta(x-j a), \quad \text { with } w>0,\] (donde\(j\) toma valores enteros), escribe expresiones explícitas para las funciones propias en la parte inferior y en la parte superior de la energía más baja banda. Boceto de ambas funciones.

2.22. Una partícula 1D de masa\(m\) se mueve en un sistema periódico infinito de pozos de potencial muy estrechos y profundos que pueden ser descritos por funciones delta:\[U(x)=w \sum_{j=-\infty}^{+\infty} \delta(x-j a), \quad \text { with } w<0 .\] (i) Esbozar la estructura de la banda de energía del sistema para valores muy pequeños y muy grandes del “peso” del pozo potencial \(|w|\), y

(ii) calcular explícitamente la energía del estado fundamental del sistema en estos dos límites.

2.23. Para el sistema discutido en el problema anterior, escribir expresiones explícitas para las funciones propias del sistema, correspondientes a:

i) la parte inferior de la banda de energía más baja,

(ii) la parte superior de esa banda, y

(iii) la parte inferior de cada banda de energía superior.

Esbozar estas funciones.

\(\underline{2.24}\). El\(1 \mathrm{D}\) “cristal” analizado en los dos últimos problemas, ahora se extiende sólo a\(x>0\), con un paso brusco a una meseta potencial plana en\(x<0\):\[U(x)= \begin{cases}w \sum_{j=1}^{+\infty} \delta(x-j a), & \text { with } w<0, \\ U_{0}>0, & \text { for } x>0,\end{cases}\] Demostrar que el sistema puede tener un conjunto de los llamados estados Tamm, localizados cerca de la “superficie” \(x=0\), y calcular sus energías en el límite cuando\(U_{0}\) es muy grande pero finito. (Cuantificar esta condición.) \({ }^{98}\)

2.25. Calcular toda la matriz de transferencia de la barrera de potencial rectangular, especificada por la Ec. (68), para las energías de partículas tanto por debajo como por encima\(U_{0}\).

2.26. Utilizar los resultados del problema anterior para calcular la matriz de transferencia de un periodo del potencial periódico de Kronig-Penney que se muestra en la Fig. 31b.

2.27. Utilizando los resultados del problema anterior, derivar las ecuaciones características para el movimiento de las partículas en el potencial periódico de Kronig-Penney, para ambos\(E<U_{0}\) y\(E>U_{0}\). Trate de llevar las ecuaciones a una forma similar a la obtenida en la Sec. 7 para las barreras delta-funcionales - ver Ec. (198). Utilice las ecuaciones para formular las condiciones de aplicabilidad de las aproximaciones de unión estrecha y potencial débil, en términos de los parámetros del sistema y la energía de la partícula\(E\).

2.28. Para el potencial de Kronig-Penney, utilice la aproximación de unión estrecha para calcular los anchos de las bandas de energía permitidas. Comparar los resultados con los del problema anterior (en el límite correspondiente).

2.29. Para el mismo potencial de Kronig-Penney, utilice las fórmulas de límite de potencial débil para calcular los anchos de brecha de energía. Nuevamente, compare los resultados con los del Problema 27, en el límite correspondiente.

2.30. Las cadenas periódicas 1D de átomos pueden exhibir lo que se llama la inestabilidad de los Peierls, lo que lleva a la transición de los Peierls a una fase en la que los átomos están ligeramente desplazados, de la periodicidad exacta, por desplazamientos alternos\(\Delta x_{j}=(-1)^{j} \Delta x\), con\(\Delta x<<a\), donde\(j\) está el número del átomo en la cadena, y\(a\) es su periodo inicial. Estos desplazamientos conducen a la alternancia de las amplitudes de acoplamiento\(\delta_{n}\) (ver Ec. (204)) entre valores cercanos\(\delta_{n}^{+}\) y\(\delta_{n}^{-}\). Utilice la aproximación de unión estrecha para calcular el cambio resultante de la banda de\(n^{\text {th }}\) energía y discutir el resultado.

2.31. "Utilice las ecuaciones (1.73) - (1.74) de las notas de clase para derivar la ecuación (252), y discutir la relación entre estas oscilaciones de Bloch y las oscilaciones de frecuencia Josephson (1.75).

2.32. Se\(m\) coloca una partícula 1D de masa en el siguiente pozo de potencial triangular:\[U(x)=\left\{\begin{array}{ll} +\infty, & \text { for } x<0, \\ F x, & \text { for } x>0, \end{array} \text { with } F>0\right. \text {. }\] (i) Calcular su espectro de energía usando la aproximación WKB.

(ii) Estimar la energía del estado fundamental utilizando el método variacional, con dos funciones de prueba diferentes.

(iii) Calcular los tres niveles de energía más bajos, y también el\(10^{\text {th }}\) nivel, con una precisión mejor que\(0.1 \%\), a partir de la solución exacta del problema.

(iv) Comparar y discutir los resultados.

Pista: Los valores de los primeros ceros de la función Airy, necesarios para Tarea (iii), se pueden encontrar en muchos manuales de matemáticas, por ejemplo, en Tabla\(9.9 .1\) de la versión en línea de la colección editada por Abramowitz y Stegun - ver MA Sec. 16 (i).

\(\underline{2.33}\). Utilice el método variacional para estimar la energía\(E_{\mathrm{g}}\) del estado fundamental de una partícula en el siguiente pozo potencial:\[U(x)=-U_{0} \exp \left\{-\alpha x^{2}\right\}, \quad \text { with } \alpha>0, \text { and } U_{0}>0 .\] Deletrear los resultados en los límites de pequeños y grandes\(U_{0}\), y dar su interpretación.

2.34. Para una partícula 1D de masa\(m\), colocada en un pozo potencial con el siguiente perfil,\[U(x)=a x^{2 s} \text {, with } a>0 \text {, and } s>0 \text {, }\] (i) calcular su espectro de energía usando la aproximación WKB, y

(ii) estimar la energía del estado fundamental utilizando el método variacional.

Compare los resultados de energía del estado del suelo para el parámetro\(s\) igual a\(1,2,3\), y 100.

2.35. Utilice el método variacional para estimar el estado\(1^{\text {st }}\) excitado del oscilador\(1 \mathrm{D}\) armónico.

2.36. Suponiendo que los efectos cuánticos sean pequeños, calcule la parte inferior del espectro de energía del siguiente sistema: una pequeña gota de masa\(m\), libre de moverse sin fricción a lo largo de un anillo de radio\(R\), que gira alrededor de su diámetro vertical con un angular constante velocidad\(\omega-\) ver la figura a la derecha. Formular una condición cuantitativa de validez de sus resultados.

Pista: Este sistema se utilizó como el “problema de banco de pruebas” de la mecánica analítica en la parte CM de esta serie, y el lector es bienvenido a usar cualquier relación derivada allí.

2.37. Un oscilador armónico 1D, con masa\(m\) y frecuencia\(\omega_{0}\), había estado en su; luego\(F\) se aplicó repentinamente una fuerza adicional, y después de eso se mantuvo constante. Calcular la probabilidad de que el oscilador permanezca en su estado fundamental.

2.38. Se colocó una partícula de masa\(m\) 1D en un pozo de potencial cuadrático (111)\[U(x)=\frac{m \omega_{0}^{2} x^{2}}{2},\] y se dejó que se relajara en el estado fundamental. Al\(t=0\), el pozo se aceleró rápidamente para moverse con velocidad\(v\), sin cambiar su perfil, de manera que en\(t \geq 0\) la fórmula anterior para\(U\) es válida con el reemplazo\(x \rightarrow\)\(x^{\prime} \equiv x-v t\). Calcular la probabilidad de que el sistema aún esté en el estado fundamental en\(t>0\). 2.39. Inicialmente, un oscilador armónico 1D estaba en su estado basal. En cierto momento, su constante de resorte\(\kappa\) se incrementa abruptamente de manera que su frecuencia\(\omega_{0}=(\kappa / m)^{1 / 2}\) se incrementa en un factor de\(\alpha\), y luego se mantiene constante en el nuevo valor. Calcular la probabilidad de que después del cambio, el oscilador se encuentre todavía en su estado fundamental.

2.40. Una partícula 1D se coloca en el siguiente pozo potencial:\[U(x)= \begin{cases}+\infty, & \text { for } x<0, \\ m \omega_{0}^{2} x^{2} / 2, & \text { for } x \geq 0 .\end{cases}\] (i) Encuentra sus funciones propias y energías propias.

(ii) Se había dejado que este sistema se relajara a su estado fundamental, y luego la pared potencial en\(x<0\) se eliminó rápidamente para que el sistema se convirtiera instantáneamente en el oscilador armónico habitual (con el mismo\(m\) y\(\omega_{0}\)). Encuentra la probabilidad de que el oscilador permanezca en su estado fundamental.

2.41. Probar la siguiente fórmula para el propagador del oscilador armónico 1D:\[G\left(x, t ; x_{0}, t_{0}\right)=\left(\frac{m \omega_{0}}{2 \pi i \hbar \sin \left[\omega_{0}\left(t-t_{0}\right)\right]}\right)^{1 / 2} \exp \left\{\frac{i m \omega_{0}}{2 \hbar \sin \left[\omega_{0}\left(t-t_{0}\right)\right]}\left[\left(x^{2}+x_{0}^{2}\right) \cos \left[\omega_{0}\left(t-t_{0}\right)\right]-2 x x_{0}\right]\right\} .\] Discutir la relación entre esta fórmula y el propagador de una partícula 1D libre.

2.42. En el contexto del teorema de oscilación de Sturm mencionado en la Sec. 9, demostrar que el número de ceros de la función propia de una partícula confinada en un pozo de potencial arbitrario pero finito siempre aumenta con la energía propia correspondiente.

Pista: Es posible que le guste usar la Ec. (186) modificada adecuadamente.

2.43. \({ }^{*}\)Utilice la aproximación WKB para calcular la vida útil del estado fundamental metaestable de una partícula 1D de masa\(m\) en el “bolsillo” del perfil potencial\[U(x)=\frac{m \omega_{0}^{2}}{2} x^{2}-\alpha x^{3} .\] Contempla la significación de este problema.

---

\({ }_{97}\)A la constante\(P\) se le llama impulso de la fuerza. (En dimensionalidades superiores, es un vector -tal como lo es la fuerza).

\({ }_{98}\)En aplicaciones a electrones en cristales de estado sólido, los pozos potenciales delta-funcionales modelan los potenciales atractivos de los núcleos atómicos, mientras que\(U_{0}\) representa la función de trabajo, es decir, la energía necesaria para la extracción de un electrón del cristal al libre espacio - véase, por ejemplo, Sec. 1.1 (ii), y también EM Sec. \(2.6\)y SM Sec. 6.3.