2.5: Movimiento en potenciales blandos

Antes de pasar a explorar otros efectos cuántico-mecánicos, veamos cómo se modifican los resultados discutidos en la sección anterior en el límite opuesto de los llamados perfiles potenciales blandos (también llamados “lisos”), como el esbozado en la Fig. \(3 .{ }^{19}\)La herramienta analítica más eficiente para estudiar este límite es la aproximación denominada WKB (o “JWKB”, o “cuasiclásica”) desarrollada por H. Jeffrey, G. Wentzel, A. Kramers y L. Brillouin en 1925-27. Para derivar su versión 1D, reescribamos la ecuación de Schrödinger (53) de una forma más simple\[\frac{d^{2} \psi}{d x^{2}}+k^{2}(x) \psi=0,\] donde el número de onda local\(k(x)\) se define de manera similar a la Ec. (65),\[k^{2}(x) \equiv \frac{2 m[E-U(x)]}{\hbar^{2}}\] además de que ahora puede ser una función de\(x\). Ya sabemos que para\(k(x)=\) const, las soluciones fundamentales de esta ecuación son\(A \exp \{+i k x\}\) y\(B \exp \{-i k x\}\), que puede representarse en una sola forma\[\psi(x)=e^{i \Phi(x)},\] donde\(\Phi(x)\) es una función compleja, en estos dos casos más simples siendo iguales, respectivamente, a\((k x-i \ln A)\) y\((-k x-i \ln B)\). Es por ello que podemos intentar usar la Eq. (83) para buscar solución de la Ec. (81) incluso en el caso general,\(k(x) \neq\) const. Diferenciando la Ec. (83) dos veces,\[\frac{d \psi}{d x}=i \frac{d \Phi}{d x} e^{i \Phi}, \quad \frac{d^{2} \psi}{d x^{2}}=\left[i \frac{d^{2} \Phi}{d x^{2}}-\left(\frac{d \Phi}{d x}\right)^{2}\right] e^{i \Phi} .\] obtenemos Conectando la última expresión\(\exp \{i \Phi(x)\}\) a la ecuación (81) y requiriendo que el factor antes desaparezca, obtenemos\[i \frac{d^{2} \Phi}{d x^{2}}-\left(\frac{d \Phi}{d x}\right)^{2}+k^{2}(x)=0 .\] Esta sigue siendo una ecuación exacta y general. A primera vista, se ve más difícil de resolver que la ecuación inicial (81), porque la ecuación (85) es no lineal. Sin embargo, está listo para la simplificación en el límite cuando el perfil potencial es muy suave,\(d U / d x \rightarrow 0\). En efecto, para un potencial uniforme,\(d^{2} \Phi / d x^{2}=0\). De ahí que en la llamada\(0^{\text {th }}\) aproximación,\(\Phi(x) \rightarrow \Phi_{0}(x)\), podamos tratar de mantener ese resultado, de manera que la Ec. (85) se reduzca a de\[\left(\frac{d \Phi_{0}}{d x}\right)^{2}=k^{2}(x), \quad \text { i.e. } \frac{d \Phi_{0}}{d x}=\pm k(x), \quad \Phi_{0}(x)=\pm i \int^{x} k\left(x^{\prime}\right) d x^{\prime},\] manera que su solución general sea una superposición lineal de dos funciones (83), con\(\Phi\) reemplazadas por \(\Phi_{0}\):\[\psi_{0}(x)=A \exp \left\{+i \int^{x} k\left(x^{\prime}\right) d x^{\prime}\right\}+B \exp \left\{-i \int^{x} k\left(x^{\prime}\right) d x^{\prime}\right\}\] donde la elección de los límites inferiores de integración afecta únicamente a las constantes\(A\) y\(B\). El sentido físico de este resultado es simple: es una suma de las ondas de Broglie que se propagan hacia adelante y hacia atrás, con el número de onda local dependiente de coordenadas\(k(x)\) que se autoajusta al perfil potencial.

Permítanme recalcar el carácter no trivial de esta aproximación. \({ }^{20}\)En primer lugar, cualquier intento de abordar el problema con el enfoque de perturbación estándar (digamos,\(\psi=\psi_{0}+\psi_{1}+\ldots\), con\(\psi_{n}\) proporcional a la\(n^{\text {th }}\) potencia de algún parámetro pequeño) fallaría para la mayoría de los potenciales, ya que como muestra la Ec. (86), incluso un ligero pero persistente desviación\(U(x)\) de una constante conduce a una acumulación gradual de la fase\(\Phi_{0}\), imposible de describir por cualquier pequeña perturbación de\(\psi\). Segundo, la caída del término\(d^{2} \Phi / d x^{2}\) en la Ec. (85) no es demasiado fácil de justificar. En efecto, dado que estamos comprometidos con el “límite de potencial blando”\(d U / d x \rightarrow 0\), debemos estar listos para asumir la longitud característica\(a\) de la variación espacial de\(\Phi\) ser grande, y descuidar los términos que son los más pequeños en el límite \(a \rightarrow \infty\). No obstante, ambos primeros términos en la ecuación (85) son aparentemente del mismo orden en\(a\), es decir\(O\left(a^{-2}\right)\); ¿por qué hemos descuidado solo uno de ellos?

El precio que hemos pagado por un tratamiento tan “descuidado” es sustancial: la ecuación (87) no satisface la propiedad fundamental de las soluciones de ecuación de Schrödinger, la conservación de la corriente de probabilidad. De hecho, dado que la Ec. (81) describe una parte espacial de energía fija (estacionaria) de la ecuación general de Schrödinger, su densidad de probabilidad\(w=\Psi \Psi^{*}=\psi \psi^{*}\), y no debe depender del tiempo. De ahí que de acuerdo con la Ec. (6), deberíamos tener\(I(x)=\) const. Sin embargo, esto no es cierto para ningún componente de la Ec. (87); por ejemplo, para el primer componente que se propaga hacia adelante en su lado derecho, la Ec. (5) arroja\[I_{0}(x)=\frac{\hbar}{m}|A|^{2} k(x),\] evidentemente no una constante si\(k(x) \neq\) const. La brillantez de la teoría WKB es que el problema puede solucionarse sin una revisión completa de la\(0^{\text {th }}\) aproximación, con sólo modificarlo. En efecto, exploremos la siguiente\(1^{\text {st }}\) aproximación:\[\Phi(x) \rightarrow \Phi_{\mathrm{WKB}}(x) \equiv \Phi_{0}(x)+\Phi_{1}(x),\] donde\(\Phi_{0}\) todavía obedece la ecuación (86), mientras que\(\Phi_{1}\) describe una corrección de\(0^{\text {th }}\) aproximación que es pequeña en el siguiente sentido:\({ }^{21}\)\[\left|\frac{d \Phi_{1}}{d x}\right|<<\left|\frac{d \Phi_{0}}{d x}\right|=k(x)\] Conectando la Eq. (89) a la Ec. (85), con la cuenta de la definición (86), obtenemos\[i\left(\frac{d^{2} \Phi_{0}}{d x^{2}}+\frac{d^{2} \Phi_{0}}{d x^{2}}\right)-\frac{d \Phi_{1}}{d x}\left(2 \frac{d \Phi_{0}}{d x}+\frac{d \Phi_{1}}{d x}\right)=0 .\] Usando la condición (90), podemos descuidar\(d^{2} \Phi_{1} / d x^{2}\) en comparación con\(d^{2} \Phi_{0} / d x^{2}\) dentro de los primeros paréntesis, y\(d \Phi_{1} / d x\) en comparación con\(2 d \Phi_{0} / d x\) dentro del segundo paréntesis. Como resultado, obtenemos lo siguiente (¡todavía aproximado!) result:\[\begin{gathered} \frac{d \Phi_{1}}{d x}=\frac{i}{2} \frac{d^{2} \Phi_{0}}{d x^{2}} / \frac{d \Phi_{0}}{d x}=\frac{i}{2} \frac{d}{d x}\left(\ln \frac{d \Phi_{0}}{d x}\right)=\frac{i}{2} \frac{d}{d x}[\ln k(x)]=i \frac{d}{d x}\left[\ln k^{1 / 2}(x)\right], \\ \left.i \Phi\right|_{\mathrm{WKB}} \equiv i \Phi_{0}+i \Phi_{1}=\pm i \int^{x} k\left(x^{\prime}\right) d x^{\prime}+\ln \frac{1}{k^{1 / 2}(x)}, \\ \psi_{\mathrm{WKB}}(x)=\frac{a}{k^{1 / 2}(x)} \exp \left\{i \int^{x} k\left(x^{\prime}\right) d x^{\prime}\right\}+\frac{b}{k^{1 / 2}(x)} \exp \left\{-i \int k\left(x^{\prime}\right) d x^{\prime}\right\} . \quad \text { for } k^{2}(x)>0 . \end{gathered}\] (Nuevamente, el límite inferior de integración es arbitrario, ya que su elección puede incorporarse a las constantes complejas\(a\) y\(b\).) Esta aproximación modificada supera el problema de la continuidad de la corriente; por ejemplo, para la onda propagadora hacia adelante, la ecuación (5) da\[I_{\mathrm{WKB}}(x)=\frac{\hbar}{m}|a|^{2}=\text { const }\] Físicamente, el factor\(k^{1 / 2}\) en el denominador del preexponente de la onda WKB es fácil de entender. Cuanto menor sea la velocidad del grupo local (32) del paquete de ondas\(v_{\mathrm{gr}}(x)=\hbar k(x) / m\), “más fácil” (más probable) debería ser encontrar la partícula dentro de un cierto intervalo\(d x\). Este es exactamente el resultado que da la aproximación WKB:\(w(x)=\psi \psi^{*} \propto 1 / k(x) \propto 1 / v_{\mathrm{gr}}\). Otro valor de la\(1^{\text {st }}\) aproximación es una aclaración de la condición de validez de la teoría WKB: viene dada por la Ec. (90). Vinculando a esta relación la primera forma de la ecuación (92), y estimando\(\left|d^{2} \Phi_{0} / d x^{2}\right|\) como\(\left|d \Phi_{0} / d x\right| / a\), donde\(a\) está la escala espacial de un cambio sustancial de\(\left|d \Phi_{0} / d x\right|=k(x)\), podemos escribir la condición como\[k a>>1 \text {. }\] En inglés llano, esto significa que el región donde\(U(x)\), y por lo tanto\(k(x)\), cambiar sustancialmente debe contener muchas longitudes de onda de Broglie\(\lambda=2 \pi / k\).

Hasta ahora he dado a entender que eso\(k^{2}(x) \propto E-U(x)\) es positivo, es decir, movimientos de partículas en la región clásicamente accesible. Ahora extendamos la aproximación WKB a situaciones donde la diferencia\(E-\)\(U(x)\) puede cambiar de signo, por ejemplo al problema de reflexión esbozado en la Fig. 3. Así como lo hicimos para el paso potencial agudo, primero necesitamos encontrar la solución adecuada en la región clásicamente prohibida, en este caso para\(x>x_{\mathrm{c}}\). Para eso, nuevamente no hay necesidad de rehacer nuestros cálculos, porque siguen siendo válidos si nosotros, al igual que en el problema del paso agudo, tomamos\(k(x)=i \kappa(x)\), dónde\[\kappa^{2}(x) \equiv \frac{2 m[U(x)-E]}{\hbar^{2}}>0, \quad \text { for } x>x_{\mathrm{c}},\] y guardamos solo una de las dos posibles soluciones (con\(\kappa>0\)), en analogía con la Ec. (58). El resultado es\[\psi_{\mathrm{WKB}}(x)=\frac{c}{\kappa^{1 / 2}(x)} \exp \left\{-\int^{x} \kappa\left(x^{\prime}\right) d x^{\prime}\right\}, \quad \text { for } k^{2}<0 \text {, i.e. } \kappa^{2}>0 \text {, }\] con el límite inferior en algún momento con\(\kappa^{2}>0\) también. ¡Esta es una fórmula realmente maravillosa! Describe la penetración cuántico-mecánica de la partícula en la región clásicamente prohibida y proporciona una generalización natural de la ecuación (58), dejando intactas nuestras estimaciones de la profundidad\(\delta \sim 1 / \kappa\) de dicha penetración. Ahora tenemos que hacer lo que hemos hecho por el problema de los pasos agudos en la Sec. 2: usar las condiciones de contorno en el punto de inflexión clásico\(x=x_{\mathrm{c}}\) para relacionar las constantes\(a, b\), y\(c\). No obstante, ahora esta operación es un poco más compleja, porque tanto las funciones WKB (94) como (98) divergen, aunque débilmente, en el punto, porque aquí ambas\(k(x)\) y\(\kappa(x)\) tienden a cero. Este problema de conexión puede resolverse de la siguiente manera. \({ }^{22}\)

Usemos nuestro compromiso con la “suavidad” del potencial, asumiendo que nos permite mantener solo dos términos principales en la expansión Taylor de la función\(U(x)\) en ese punto\(x_{\mathrm{c}}\):\[U(x) \approx U\left(x_{\mathrm{c}}\right)+\left.\frac{d U}{d x}\right|_{x=x_{\mathrm{c}}}\left(x-x_{\mathrm{c}}\right) \equiv E+\left.\frac{d U}{d x}\right|_{x=x_{\mathrm{c}}}\left(x-x_{\mathrm{c}}\right) .\] Usando esta expansión truncada, e introduciendo la siguiente variable adimensional para la desviación de la coordenada del punto de inflexión clásico,\[\zeta \equiv \frac{x-x_{\mathrm{c}}}{x_{0}}, \quad \text { with } x_{0} \equiv\left[\frac{\hbar^{2}}{2 m(d U / d x)_{x=x_{\mathrm{c}}}}\right]^{1 / 3} \text {, }\] reducimos la ecuación de Schrödinger (81) a la denominada ecuación Airy

\[\ \text{Airy equation}\quad\quad\quad\quad\frac{d^{2} \psi}{d \zeta^{2}}-\zeta \psi=0.\]

Esta ecuación diferencial simple lineal, ordinaria y homogénea de segundo orden ha sido muy bien estudiada. Su solución general puede representarse como una combinación lineal de dos soluciones fundamentales, las funciones\(\operatorname{Ai}(\zeta)\) Airy y\(\operatorname{Bi}(\zeta)\), mostradas en la Fig. \(9 \mathrm{a} .23\)

Fig. 2.9. (a) Las funciones Airy Ai y Bi, y (b) la aproximación WKB para la función\(\operatorname{Ai}(\zeta)\).

Esta última función diverge en\(\zeta \rightarrow+\infty\), y por lo tanto no es adecuada para nuestro problema actual (Fig. 3), mientras que la primera función tiene los siguientes comportamientos asintóticos en\(|\zeta|>>1\):\[\operatorname{Ai}(\zeta) \rightarrow \frac{1}{\pi^{1 / 2}|\zeta|^{1 / 4}} \times \begin{cases}\frac{1}{2} \exp \left\{-\frac{2}{3} \zeta^{3 / 2}\right\}, & \text { for } \zeta \rightarrow+\infty \\ \sin \left\{\frac{2}{3}(-\zeta)^{3 / 2}+\frac{\pi}{4}\right\}, & \text { for } \zeta \rightarrow-\infty\end{cases}\] Ahora apliquemos la aproximación WKB a la ecuación Airy (101). Tomando el punto de inflexión clásico\((\zeta=0)\) para el límite inferior, pues\(\zeta>0\) obtenemos\[\kappa^{2}(\zeta)=\zeta, \quad \kappa(\zeta)=\zeta^{1 / 2}, \quad \int_{0}^{\zeta} \kappa\left(\zeta^{\prime}\right) d \zeta^{\prime}=\frac{2}{3} \zeta^{3 / 2},\] i.e., exactamente el exponente en la línea superior de la Ec. (102). Haciendo un cálculo similar para\(\zeta<0\), con la suposición natural\(|b|=|a|\) (reflexión completa del paso potencial), llegamos al siguiente resultado:\[\operatorname{Ai}_{\mathrm{WKB}}(\zeta)=\frac{1}{|\zeta|^{1 / 4}} \times \begin{cases}c^{\prime} \exp \left\{-\frac{2}{3} \zeta^{3 / 2}\right\}, & \text { for } \zeta>0, \\ a^{\prime} \sin \left\{\frac{2}{3}(-\zeta)^{3 / 2}+\varphi\right\}, & \text { for } \zeta<0 .\end{cases}\] Esta aproximación difiere de la solución exacta a valores pequeños de\(\zeta\), es decir, cerrar al punto de inflexión clásico\(-\) ver Fig. \(9 \mathrm{~b}\). Sin embargo, at\(|\zeta|>>1\), Eqs. (104) describen exactamente la función Airy, siempre que\[\varphi=\frac{\pi}{4}, \quad c^{\prime}=\frac{a^{\prime}}{2} .\] estas fórmulas de conexión puedan usarse para reescribir la ecuación (104) como\[\mathrm{Ai}_{\mathrm{wKB}}(\zeta)=\frac{a^{\prime}}{2|\zeta|^{1 / 4}} \times\left\{\frac{\exp \left\{-\frac{2}{3} \zeta^{3 / 2}\right\},}{\frac{1}{i}\left[\exp \left\{+i \frac{2}{3} \zeta^{3 / 2}+i \frac{\pi}{4}\right\}-\exp \left\{-i \frac{2}{3} \zeta^{3 / 2}-i \frac{\pi}{4}\right\}\right],} \quad \text { for } \zeta<0,\right.\] y por lo tanto pueden ser descritas por las siguientes dos reglas mnemotécnicas simples:

(i) Si se toma el punto de inflexión clásico para el límite inferior en las integrales WKB en las regiones clásicamente permitidas y clásicamente prohibidas, entonces los módulos de las cuasiamplitudes de los exponentes son iguales.

(ii) Reflejando a partir de un escalón potencial “suave”, la función de onda adquiere un desplazamiento de fase adicional\(\Delta \varphi=\pi / 2\), si se compara con su reflexión de un muro de potencial “duro”, infinitamente alto ubicado en un punto\(x_{\mathrm{c}}\) (para lo cual, según la Ec. (63) con\(\kappa=0\), tenemos \(B=-A\)).

Para que las fórmulas de conexión (105) - (106) sean válidas, las desviaciones de la aproximación lineal\((99)\) del perfil potencial deben ser relativamente pequeñas dentro de la región donde la aproximación WKB difiere de la función Airy exacta:\(|\zeta| \sim 1\), i.e. \(\left|x-x_{\mathrm{c}}\right| \sim x_{0}\). Estas desviaciones pueden estimarse utilizando el siguiente término de la expansión de Taylor, caída en la Ec. (99):\(\left(d^{2} U / d^{2} x\right)\left(x-x_{\mathrm{c}}\right)^{2} / 2\). Como resultado, la condición de validez de las fórmulas de conexión (es decir, de la “suavidad” del perfil de potencial reflectante) puede expresarse como\(\left|d^{2} U / d^{2} x\right|<<|d U / d x|\) en el\(x \approx x_{\mathrm{c}}-\) sentido de la\(\sim x_{0}-\) amplia proximidad del punto\(x_{\mathrm{c}}\)). Con la cuenta de la Ec. (100) for\(x_{0}\), esta condición se vuelve\[\left|\frac{d^{2} U}{d x^{2}}\right|_{x \approx x_{\mathrm{c}}}^{3}<<\frac{2 m}{\hbar^{2}}\left(\frac{d U}{d x}\right)_{x \approx x_{\mathrm{c}}}^{4}\] Como ejemplo de una aplicación muy útil de la aproximación WKB, usemos las fórmulas de conexión para calcular el espectro de energía de una partícula 1D en un pozo de potencial 1D blando (Fig. 10).

Fig. 2.10. El tratamiento WKB de un estado propio de una partícula en un pozo de\(1 \mathrm{D}\) potencial blando.

Como se discutió en la Sec. 1.7, podemos considerar la onda estacionaria que describe una función propia\(\psi_{n}\) (correspondiente a una energía propia\(E_{n}\)) como una suma de dos ondas viajeras de Broglie que van y vienen entre las paredes, siendo reflejadas secuencialmente desde cada una de ellas. Apliquemos la aproximación WKB a tales olas viajeras. Primero, de acuerdo con la Ec. (94), propagándose desde el punto de inflexión clásico izquierdo\(x_{\mathrm{L}}\) a la derecha tal punto\(x_{R}\), adquiere el cambio de fase\[\Delta \varphi_{\rightarrow}=\int_{x_{\mathrm{L}}}^{x_{\mathrm{R}}} k(x) d x .\] Al reflejo de la pared blanda en\(x_{R}\), según la regla mnemotécnica (ii), la onda adquiere un turno adicional\(\pi / 2\). Ahora, viajando de regreso de\(x_{\mathrm{R}}\) a\(x_{\mathrm{L}}\), la ola obtiene un turno similar al dado por la Ec. (108):\(\Delta \varphi_{\leftarrow}=\Delta \varphi_{\rightarrow}\). Por último, a la reflexión de\(x_{\mathrm{L}}\) ella obtiene un\(\pi / 2\) turno más. Resumiendo todas estas contribuciones en el viaje de ida y vuelta de la ola, podemos escribir la condición de autoconsistencia (que la función de onda “atrapa su propia cola con sus dientes”) en la forma\[\Delta \varphi_{\text {total }} \equiv \Delta \varphi_{\rightarrow}+\frac{\pi}{2}+\Delta \varphi_{\leftarrow}+\frac{\pi}{2} \equiv 2 \int_{x_{\mathrm{L}}}^{x_{\mathrm{R}}} k(x) d x+\pi=2 \pi n, \quad \text { with } n=1,2, \ldots\] Reescribiendo este resultado en términos del impulso de la partícula\(p(x)=\hbar k(x)\), llegamos a la llamada WilsonSommerfeld (o “Bohr-Sommerfeld”) regla de cuantificación\[\oint_{C} p(x) d x=2 \pi \hbar\left(n-\frac{1}{2}\right),\] donde el camino cerrado\(C\) significa el período completo del movimiento clásico. \({ }^{24}\)

Veamos qué da esta regla de cuantificación para el muy importante caso particular de un perfil de potencial cuadrático de un oscilador armónico de frecuencia\(\omega_{0}\). En este caso,\[U(x)=\frac{m}{2} \omega_{0}^{2} x^{2},\] y los puntos de inflexión clásicos (donde\(U(x)=E\)) son las raíces de una ecuación simple\[\frac{m}{2} \omega_{0}^{2} x_{\mathrm{c}}^{2}=E_{n}, \quad \text { so that } x_{\mathrm{R}}=\frac{1}{\omega_{0}}\left(\frac{2 E_{n}}{m}\right)^{1 / 2}>0, \quad x_{\mathrm{L}}=-x_{\mathrm{R}}<0 .\] Debido a la simetría del potencial, la integración requerida por la Ec. (110) también es simple: de\[\begin{aligned} \int_{x_{\mathrm{L}}}^{x_{\mathrm{R}}} p(x) d x &=\int_{x_{\mathrm{L}}}^{x_{\mathrm{R}}}\left\{2 m\left[E_{n}-U(x)\right]\right\}^{1 / 2} d x \equiv\left(2 m E_{n}\right)^{1 / 2} 2 \int_{0}^{x_{\mathrm{R}}}\left(1-\frac{x^{2}}{x_{\mathrm{R}}^{2}}\right)^{1 / 2} d x \\ & \equiv\left(2 m E_{n}\right)^{1 / 2} 2 x_{\mathrm{R}} \int_{0}^{1}\left(1-\xi^{2}\right)^{1 / 2} d \xi=\left(2 m E_{n}\right)^{1 / 2} 2 x_{\mathrm{R}} \frac{\pi}{4} \equiv \frac{\pi E_{n}}{\omega_{0}} \end{aligned}\] manera que la Ec. (110) rinde\[E_{n}=\hbar \omega_{0}\left(n^{\prime}+\frac{1}{2}\right), \quad \text { with } n^{\prime} \equiv n-1=0,1,2, \ldots .\] Para estimar la validez de este resultado , tenemos que verificar la condición (96) en todos los puntos de la región clásicamente permitida, y la Eq. (107) en los puntos de inflexión. El chequeo muestra que ambas condiciones son válidas sólo para\(n \gg>1\). Sin embargo, veremos en la Sec. 9 a continuación que la Ec. (114) es realmente exactamente correcta para todos los niveles de energía, gracias a las propiedades especiales del perfil potencial (111).

Ahora usemos la regla mnemotécnica (i) para examinar la penetración de partículas en la región clásicamente prohibida de un escalón potencial abrupto de una altura\(U_{0}>E\). Para este caso, la regla, es decir, la segunda de las ecuaciones (105), arroja la siguiente relación de las cuasiamplitudes en las ecuaciones (94) y (98):\(|c|=|a| / 2\). Si ahora aplicáramos ingenuamente esta relación al paso agudo esbozado en la Fig. 4, olvidando que no satisface la ecuación (107), obtendríamos la siguiente relación de las amplitudes completas, definidas por las ecuaciones (55) y (58):\[\left|\frac{C}{\kappa}\right|=\frac{1}{2}\left|\frac{A}{k}\right| . \quad \text { (WRONG!) }\] Este resultado difiere de la ecuación correcta (63), y de ahí podemos esperar que el WKB La predicción de aproximación para potenciales más complejos, lo más importante para tunelización a través de una barrera de potencial blando (Fig. 11) también debe ser diferente del resultado exacto (71) para la barrera rectangular mostrada en la Fig. 6.

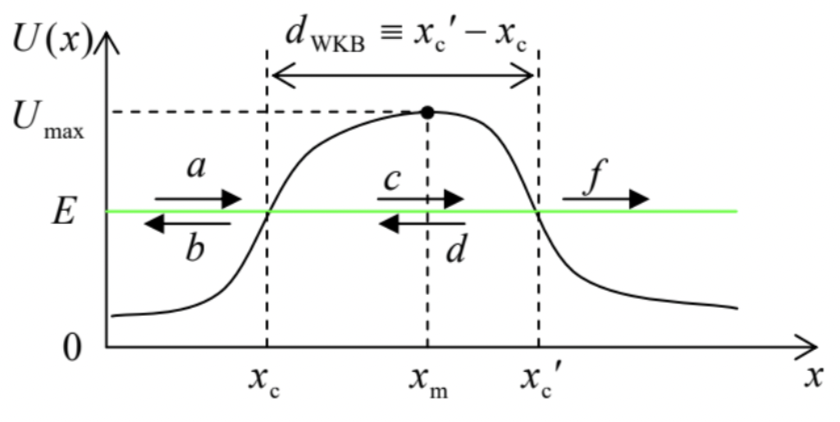Fig. 2.11. Túnel a través de una barrera de potencial 1D suave.

Para analizar la tunelización a través de una barrera tan blanda, necesitamos (al igual que en el caso de una barrera rectangular) tomar en consideración cinco ondas parciales, pero ahora deben tomarse en forma WKB:\[\psi_{\mathrm{WKB}}= \begin{cases}\frac{a}{k^{1 / 2}(x)} \exp \left\{\frac{c}{\kappa^{1 / 2}(x)} \exp \left\{-\int^{x} k\left(x^{\prime}\right) d x^{\prime}\right\}+\frac{b}{k^{1 / 2}(x)} \exp \left\{-i \int^{x} k\left(x^{\prime}\right) d x^{\prime}\right\},\right. & \text { for } x<x_{\mathrm{c}}, \\ \frac{f}{k^{1 / 2}(x)} \exp \left\{\frac{d}{i \int k\left(x^{\prime}\right) d x^{\prime}}\right\}, & \text { for } x_{\mathrm{c}}<x<x_{\mathrm{c}}^{\prime}, \\ & \text { for } x_{\mathrm{c}}^{\prime}<x,\end{cases}\] donde los límites inferiores de integrales son arbitrarios (cada una dentro del rango correspondiente de \(x\)). Ya que a la derecha del punto clásico izquierdo, tenemos dos exponentes en lugar de uno, y a la derecha del segundo punto, una onda viajera en lugar de dos, las fórmulas de conexión (105) tienen que generalizarse, utilizando fórmulas asintóticas no solo para\(\operatorname{Ai}(\zeta)\), sino también para el segundo \(\operatorname{Airy}\)función,\(\operatorname{Bi}(\zeta)\). El análisis, absolutamente similar al realizado anteriormente (aunque naturalmente un poco más voluminoso),\({ }^{25}\) da un resultado notablemente simple:\[\mathscr{T}_{\mathrm{WKB}} \equiv\left|\frac{f}{a}\right|^{2}=\exp \left\{-2 \int_{x_{\mathrm{c}}}^{x_{\mathrm{c}}^{\prime}} \kappa(x) d x\right\} \equiv \exp \left\{-\frac{2}{\hbar} \int_{x_{\mathrm{c}}}^{x_{\mathrm{c}}^{\prime}}(2 m[U(x)-E])^{1 / 2} d x\right\}\] con el factor preexponencial igual a 1, el hecho que podría esperarse fácilmente de la regla mnemónica (i) de las fórmulas de conexión.

Esta fórmula es ampliamente utilizada en la mecánica cuántica aplicada, a pesar del carácter aproximado de su coeficiente preexponencial para barreras insuficientemente blandas que no satisfacen la Ec. (107). Por ejemplo, la Ec. (80) muestra que para una barrera rectangular con espesor\(d \gg>\delta\), la aproximación WKB (117) con\(d_{\mathrm{WKB}}=d\) subestimaciones\(\mathscr{T}\) por un factor de\(\left[4 k \kappa /\left(k^{2}+\kappa^{2}\right)\right]^{2}-\) igual, por ejemplo, 4, si, es decir\(k=\kappa\), si \(U_{0}=2 E\). Sin embargo, en la escala logarítmica apropiada (ver Fig. 7b), dicho factor, menor que un orden de magnitud, es solo una pequeña corrección.

Obsérvese también que cuando se\(E\) acerca a la parte superior de la barrera\(U_{\max }\) (Fig. 11), los puntos\(x_{\mathrm{c}}\) y\(x_{\mathrm{c}}\) 'se funden, de manera que según la Ec. (117)\(\mathscr{T}_{\text {WKB }} \rightarrow 1\), es decir, la reflexión de la partícula se desvanece en\(E=U_{\text {max }}\). Entonces, la aproximación WKB no describe el efecto de la reflexión sobre barrera en\(E>U_{\max }\). (Este hecho podría notarse ya a partir de la Ec. (95): en ausencia de los puntos de inflexión clásicos, la corriente de probabilidad WKB es constante para cualquier perfil de barrera.) Esta conclusión es incorrecta incluso para barreras aparentemente suaves donde uno podría esperar ingenuamente que la aproximación WKB funcione perfectamente. De hecho, cerca del punto\(x=x_{\mathrm{m}}\) donde el potencial alcanza el máximo (i.e.\(U\left(x_{\mathrm{m}}\right)=U_{\max }\)), siempre podemos aproximar cualquier función suave\(U(x)\) con el término cuadrático de la expansión de Taylor, es decir, con una parábola invertida:\[U(x) \approx U_{\max }-\frac{m \omega_{0}^{2}\left(x-x_{\mathrm{m}}\right)^{2}}{2} .\] Calculando derivadas \(d U / d x\)y\(d^{2} U / d x^{2}\) de esta función y conectándolos a la condición\((107)\), podemos ver que la aproximación WKB sólo es válida si\(\left|U_{\max }-E\right| \gg>\hbar \omega_{0}\). Solo para la referencia del lector, un análisis exacto de la tunelización a través de la barrera (118) da la siguiente fórmula de Kemble: 26\[\mathscr{T}=\frac{1}{1+\exp \left\{-2 \pi\left(E-U_{\max }\right) / \hbar \omega_{0}\right\}},\] válida para cualquier signo de la diferencia\(\left(E-U_{\max }\right) .\) Esta fórmula describe un enfoque gradual de\(\mathscr{T}\) a 1, es decir, una reducción gradual de reflexión, al aumento de la energía de las partículas, con\(\mathscr{T}=1 / 2\) at\(E=U_{\max }\).

El último comentario de esta sección: la aproximación WKB abre un camino recto hacia una formulación alternativa de la mecánica cuántica, basada en el camino de Feynman integral. No obstante, pospondré su discusión hasta que se haya introducido una notación más compacta en el Capítulo\(4 .\)

---

\({ }^{19}\)Las condiciones cuantitativas de la “suavidad” se formularán posteriormente en esta sección.

\({ }^{20}\)Filosóficamente, este método de dominio espacial está muy cerca del método de van der Pol en el dominio del tiempo en la mecánica clásica, y la aproximación de onda giratoria (RWA) muy similar en la mecánica cuántica - véase, por ejemplo, CM Secs. \(5.2-5.5\), y también Secs. \(6.5,7.6,9.2\), y\(9.4\) de este curso.

\({ }^{21}\)Para mayor certeza, utilizaré la discrecionalidad dada por la ecuación (82) para definir\(k(x)\) como la raíz positiva de su lado derecho.

\({ }^{22}\)Una forma alternativa de resolver el problema de conexión, sin involucrar las funciones Airy pero utilizando una extensión analítica de fórmulas WKB al plano de argumentos complejos, se puede encontrar, por ejemplo, en la Sec. 47 del libro de texto de L. Landau y E. Lifshitz, Mecánica Cuántica, Teoría no Relativista, 3ª ed. Pérgamo,\(1977 .\)

\({ }^{23}\)Tenga en cuenta las siguientes fórmulas integrales (exactas),

\(\operatorname{Ai}(\zeta)=\frac{1}{\pi} \int_{0}^{\infty} \cos \left(\frac{\xi^{3}}{3}+\zeta \xi\right) d \xi, \quad \operatorname{Bi}(\zeta)=\frac{1}{\pi} \int_{0}^{\infty}\left[\exp \left\{-\frac{\xi^{3}}{3}+\zeta \xi\right\}+\sin \left(\frac{\xi^{3}}{3}+\zeta \xi\right)\right] d \xi,\)

frecuentemente más conveniente para los cálculos prácticos de las funciones Airy que la ecuación diferencial (101).

\({ }^{24}\)Tenga en cuenta que en el movimiento en más de una dimensión, una trayectoria clásica cerrada puede no tener puntos de inflexión clásicos. En este caso, la constante\(1 / 2\), que surge de los giros, debe descartarse de las ecuaciones (110) escritas para el producto\(\mathbf{p}(\mathbf{r}) \cdot d \mathbf{r}\) escalar, la llamada regla de cuantificación de Bohr. Fue sugerido por N. Bohr ya en 1913 como una interpretación de la ecuación (1.8) para el movimiento circular del electrón alrededor del protón, mientras que su modificación 1D (110) se debe a W. Wilson (1915) y A. Sommerfeld (1916).

\({ }^{25}\)Para el caso más importante\(\mathcal{T}_{\text {WKB }}<<1\), la ecuación (117) puede derivarse simplemente de las ecuaciones (105) - (106) - el ejercicio dejado para el lector.

\({ }^{26}\)Esta fórmula fue derivada (en una forma más general, válida para una barrera arbitraria de potencial blando) por E. Kemble en 1935. En algunas comunidades, se le conoce como la “fórmula Hill-Wheeler”, según el artículo de 1953 de D. Hill y J. Wheeler en que la fórmula de Kemble se detalló para el perfil cuadrático (118). Obsérvese que matemáticamente la Ec. (119) es similar a la distribución de Fermi en física estadística, con una temperatura efectiva\(T_{\text {ef }}=\hbar \omega_{0} / 2 \pi k_{\text {B }}\). Esta coincidencia tiene algunas implicaciones curiosas para las estadísticas de túnel de partículas de Fermi.