2.7:2.6. Acoplamiento de Estado Localizado y Oscilaciones Cuánticas

Ahora vamos a discutir un efecto más específico de la mecánica cuántica. Su descripción matemática puede simplificarse utilizando un potencial modelo que consiste en dos pozos de potencial muy cortos y profundos. Para ello, analicemos primero las propiedades de un solo pozo de este tipo (Fig. 18), que pueden modelarse de manera similar a la barrera de potencial corto y alto - ver Eq. (74), pero con un “peso” negativo:\[U(x)=-w \delta(x), \quad \text { with } w>0 .\]

En contraste con su contraparte de barrera de túnel (74), dicho potencial sostiene un estado estacionario con una autoenergía negativa\(E<0\), y una función propia localizada\(\psi\), con\(|\psi| \rightarrow 0\) at\(x \rightarrow \pm \infty\).

Fig. \(2.18\). Pozo de potencial delta funcional y su propio estado localizado (esquemáticamente).

En efecto, en\(x \neq 0, U(x)=0\), así la ecuación de\(1 \mathrm{D}\) Schrödinger se reduce a la ecuación de Helmholtz (1.83), cuyas soluciones localizadas con\(E<0\) son exponentes únicos, desapareciendo a grandes distancias:\({ }^{38}\)\[\psi(x)=\psi_{0}(x) \equiv\left\{\begin{array}{ll} A e^{-\kappa x}, & \text { for } x>0, \\ A e^{+\kappa x}, & \text { for } x<0, \end{array} \quad \text { with } \frac{\hbar^{2} \kappa^{2}}{2 m}=-E, \quad \kappa>0 .\right.\] (Los coeficientes ante los exponentes han sido seleccionados iguales para satisfacer la condición límite (76) de la continuidad de la función de onda en\(x=0\).) Conectando la Eq. (159) a la segunda condición de límite, dada por la Ec. (75), pero ahora con el signo negativo anterior\(w\), obtenemos\[(-\kappa A)-(+\kappa A)=-\frac{2 m w}{\hbar^{2}} A,\] en la que se\(A \neq 0\) puede cancelar el factor común. Esta ecuación\({ }^{39}\) tiene una solución para cualquiera\(w>0\):\[\kappa=\kappa_{0} \equiv \frac{m w}{\hbar^{2}},\] y por lo tanto el sistema tiene solo un estado localizado (tierra), con la siguiente energía propia: 40\[E=E_{0} \equiv-\frac{\hbar^{2} \kappa_{0}^{2}}{2 m}=-\frac{m w^{2}}{2 \hbar^{2}} .\] Ahora estamos listos para analizar estados localizados del potencial de dos pozos que se muestra en la Fig. 19: \[U(x)=-w\left[\delta\left(x-\frac{a}{2}\right)+\delta\left(x+\frac{a}{2}\right)\right], \quad \text { with } w>0 .\]Aquí todavía podemos usar las soluciones de exponente único, similares a la Ec. (159), para la función de onda fuera del intervalo\([-a / 2,+a / 2]\), pero dentro del intervalo, debemos tener en cuenta ambos exponentes posibles:\[\psi=C_{+} e^{\kappa x}+C_{-} e^{-\kappa x} \equiv C_{\mathrm{A}} \sinh \kappa x+C_{\mathrm{S}} \cosh \kappa x, \quad \text { for }-\frac{a}{2} \leq x \leq+\frac{a}{2},\] con el parámetro\(\kappa\) definido como en la Ec. ( 159). La última de estas expresiones equivalentes es más conveniente porque debido a la simetría del potencial (163) al punto central\(x=0\), las funciones propias del sistema deben ser funciones simétricas (pares) o antisimétricas (impares) de\(x\) (ver Fig. 19), para que puedan analizarse por separado, solo para la mitad del sistema, digamos\(x \geq 0\), y usando solo una de las funciones hiperbólicas (164) en cada caso.

Fig. 2.19. Un sistema de dos pozos potenciales acoplados, y sus propios estados localizados (esquemáticamente).

Para la función propia antisimétrica, las ecuaciones (159) y (164) rinden\[\psi_{\mathrm{A}} \equiv C_{\mathrm{A}} \times\left\{\begin{array}{lr} \sinh \kappa x, & \text { for } 0 \leq x \leq \frac{a}{2}, \\ \sinh \frac{\kappa a}{2} \exp \left\{-\kappa\left(x-\frac{a}{2}\right)\right\}, & \text { for } \frac{a}{2} \leq x, \end{array}\right.\] donde se ha seleccionado el coeficiente frontal en la línea inferior para satisfacer la condición (76) de continuidad de la función ondulada en\(x=+a / 2-\) y por lo tanto at\(x=-a / 2\). Lo que queda es satisfacer la condición (75), con un signo negativo antes\(w\), para el salto del derivado en ese punto. Esta condición produce la siguiente ecuación característica:\[\sinh \frac{\kappa a}{2}+\cosh \frac{\kappa a}{2}=\frac{2 m w}{\hbar^{2} \kappa} \sinh \frac{\kappa a}{2}, \quad \text { i.e. } 1+\operatorname{coth} \frac{\kappa a}{2}=2 \frac{\left(\kappa_{0} a\right)}{(\kappa a)},\] donde\(\kappa_{0}\), dada por la Ec. (161), es el valor de\(\kappa\) para un solo pozo, es decir, el ancho espacial recíproco de su función propia localizada - ver Fig. 18.

La Figura 20a muestra ambos lados de la ecuación (166) como funciones del producto adimensional\(\kappa a\), para varios valores del parámetro\(\kappa_{0} a\), es decir, de la distancia normalizada entre los dos pocillos. Las gráficas muestran, en primer lugar, que a medida que disminuye el parámetro, las gráficas LHS y RHS\(\kappa_{0} a\) se cruzan (es decir, la Ec. (166) tiene una solución) a valores menores y menores de\(\kappa a\). En\(\kappa a<<1\), el lado izquierdo de la última forma de esta ecuación puede aproximarse como\(2 / \kappa a\). Comparando esta expresión con el lado derecho de la ecuación característica, vemos que esta ecuación trascendental tiene una solución (es decir, el sistema tiene un estado localizado antisimétrico) solo si\(\kappa_{0} a>1\), es decir, si la distancia\(a\) entre los dos pozos potenciales estrechos es mayor que el siguiente valor,\[a_{\min }=\frac{1}{\kappa_{0}} \equiv \frac{\hbar^{2}}{m w},\] que es igual a la dispersión característica de la función ondulada en un solo pozo - ver Fig. 18. (At\(a \rightarrow\)\(a_{\min }, \kappa a \rightarrow 0\), lo que significa que la localización del estado se vuelve cada vez más débil.)

(a) el eigenstate antisimétrico (165), y (b) el eigenstate simétrico (171).

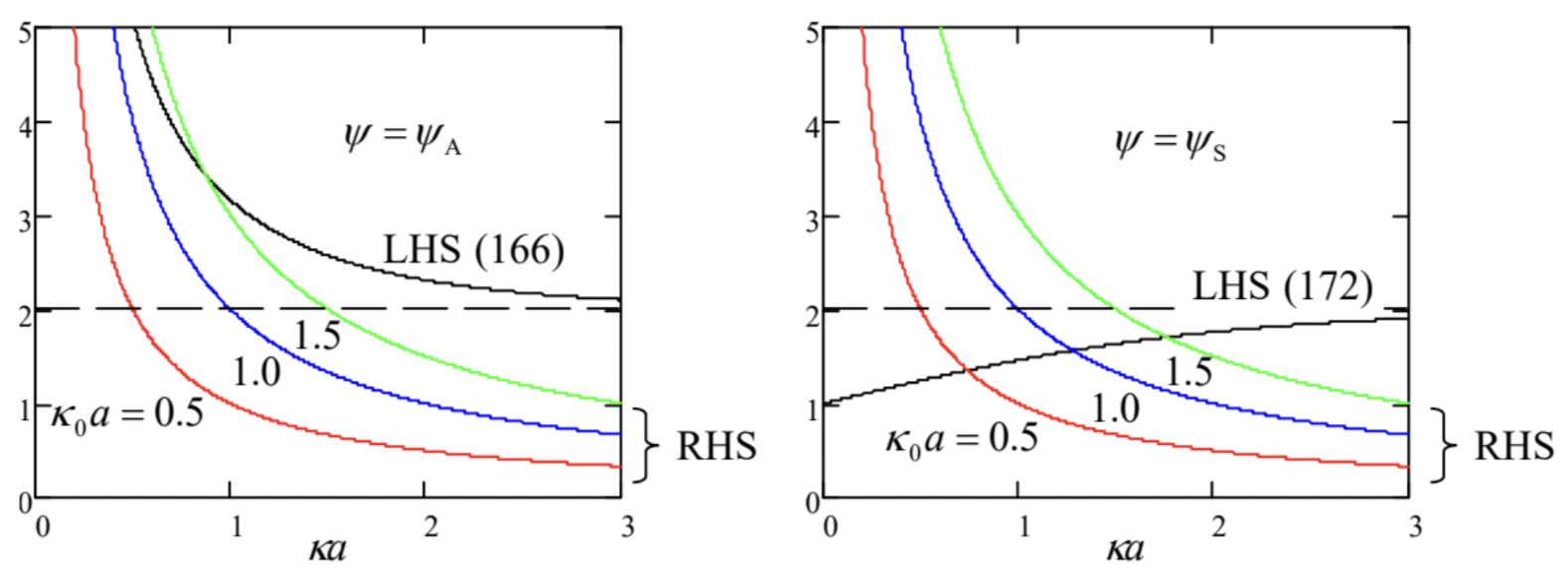
En el límite opuesto de grandes distancias entre los pozos potenciales, es decir\(\kappa_{0} a \gg 1\), la ecuación (166) muestra que\(\kappa a>>1\) también, de manera que su lado izquierdo puede aproximarse como\(2(1+\exp \{-\kappa a\})\), y la ecuación rinde\[\kappa \approx \kappa_{0}\left(1-\exp \left\{-\kappa_{0} a\right\}\right) \approx \kappa_{0} .\] Este resultado significa que la función propia es una superposición antisimétrica de dos ondas virtualmente imperturbadas (159) de cada pozo de potencial parcial:\[\psi_{\mathrm{A}}(x) \approx \frac{1}{\sqrt{2}}\left[\psi_{\mathrm{R}}(x)-\psi_{\mathrm{L}}(x)\right], \quad \text { where } \psi_{\mathrm{R}}(x) \equiv \psi_{0}\left(x-\frac{a}{2}\right), \quad \psi_{\mathrm{L}}(x) \equiv \psi_{0}\left(x+\frac{a}{2}\right),\] y el coeficiente frontal se selecciona de tal manera que si se normaliza la función\(\psi_{0}\) propia de cada pozo, así es\(\psi_{\mathrm{A}}\). Conectando la forma media (más exacta) de la Eq. (168) en la última de las ecuaciones (159), podemos ver que en este límite la energía del estado antisimétrico es solo ligeramente superior a la energía propia\(E_{0}\) de un solo pozo, dada por la ecuación (162):\[E_{\mathrm{A}} \approx E_{0}\left(1-2 \exp \left\{-\kappa_{0} a\right\}\right) \equiv E_{0}+\delta, \quad \text { where } \delta \equiv \frac{2 m w^{2}}{\hbar^{2}} \exp \left\{-\kappa_{0} a\right\}>0 .\] La función propia simétrica tiene una forma que recuerda Eq. (165), pero aún diferente de ella:\[\psi=\psi_{\mathrm{S}} \equiv C_{\mathrm{S}} \times\left\{\begin{array}{lr} \cosh \kappa x, & \text { for } 0 \leq x \leq \frac{a}{2}, \\ \cosh \frac{\kappa a}{2} \exp \left\{-\kappa\left(x-\frac{a}{2}\right)\right\}, & \text { for } \frac{a}{2} \leq x, \end{array}\right.\] dando una ecuación característica similar en estructura a la Ec. (166), pero con un lado izquierdo diferente:\[1+\tanh \frac{\kappa a}{2}=2 \frac{\left(\kappa_{0} a\right)}{(\kappa a)} \text {. }\] La figura\(20 \mathrm{~b}\) muestra ambos lados de esta ecuación para varios valores del parámetro\(\kappa_{0} a\). Es evidente que en contraste con la Ec. (166), la ecuación (172) tiene una solución única (y por lo tanto el sistema tiene un eigenstate simétrico localizado) para cualquier valor del parámetro\(\kappa_{0} a\), es decir, para cualquier distancia entre los pozos parciales. En el límite de pozos muy cercanos (es decir, su fuerte acoplamiento)\(\kappa_{0} a<<1\), obtenemos\(\kappa a<<1\),\(\tanh (\kappa a / 2) \rightarrow 0\), y Eq. (172) rendimientos\(\kappa \rightarrow 2 \kappa_{0}\), lo que lleva a un aumento cuádruple de la magnitud de la energía propia en comparación con la del pozo único: \[E_{\mathrm{S}} \approx 4 E_{0} \equiv-\frac{m(2 w)^{2}}{2 \hbar^{2}}, \quad \text { for } \kappa_{0} a<<1 .\]El significado físico de este resultado es muy simple: dos pozos potenciales muy cercanos actúan (¡solo sobre la función propia simétrica!) juntos, para que sus “pesos”\(w \equiv \int U(x) d x\) solo sumen.

\(\kappa a>>1\)Al contrario, el límite de acoplamiento débil\(\kappa_{0} a>>1\), es decir, la ecuación (172) muestra que también, de manera que su lado izquierdo puede aproximarse como\(2(1-\exp \{-\kappa a\})\), y la ecuación rinde\[\kappa \approx \kappa_{0}\left(1+\exp \left\{-\kappa_{0} a\right\}\right) \approx \kappa_{0} .\] En este límite, la función propia es una superposición simétrica de dos virtualmente ondas imperturbadas (159) de cada pozo potencial parcial:\[\psi_{\mathrm{S}}(x) \approx \frac{1}{\sqrt{2}}\left[\psi_{\mathrm{R}}(x)+\psi_{\mathrm{L}}(x)\right],\] y la energía propia también está cerca de la energía\(E_{0}\) de un pozo parcial, pero es ligeramente inferior:\[E_{\mathrm{S}} \approx E_{0}\left(1+2 \exp \left\{-\kappa_{0} a\right\}\right) \equiv E_{0}-\delta, \quad \text { so that } E_{\mathrm{A}}-E_{\mathrm{S}}=2 \delta,\] donde\(\delta\) vuelve a ser dada por la última de las Eq. (170).

Entonces, la energía propia del estado simétrico es siempre menor que la del estado antisimétrico. La física de este efecto (que permanece cualitativamente igual en sistemas de dos componentes más complejos, lo más importante en moléculas diatómicas como\(\mathrm{H}_{2}\)) es evidente a partir del boceto de las funciones de onda\(\psi_{\mathrm{A}}\) y\(\psi_{\mathrm{s}}\), dado por las ecuaciones (165) y (171), en Fig. 19. En el modo antisimétrico, la función de onda tiene que desaparecer en el centro del sistema, de manera que cada mitad se exprime a la mitad de la extensión espacial del sistema. Tal apretón aumenta el gradiente de la función, y de ahí su energía cinética (1.27), y de ahí su energía total. Por el contrario, en el modo simétrico, la función de onda se propaga efectivamente en el pozo de contraparte. Como resultado, cambia en el espacio más lento, y de ahí su energía cinética también es menor.

Aún más importante, la energía del estado simétrico disminuye a medida que disminuye la distancia\(a\), lo que corresponde a la atracción efectiva de los pozos parciales. Este es un buen modelo de juguete del tipo de cohesión atómica más fuerte (y lo más importante): la unión covalente (o “química”). \({ }^{41}\)En el caso más simple de la\(\mathrm{H}_{2}\) molécula, cada uno de los dos electrones del sistema, en su estado fundamental,\({ }^{42}\) reduce su energía cinética al extender su función de onda alrededor de ambos núcleos de hidrógeno (protones), en lugar de estar confinado cerca de uno de ellos -como tenía que estar en un solo átomo. El enlace resultante es muy fuerte: en unidades químicas, es decir\(429 \mathrm{~kJ} / \mathrm{mol}\),\(18.6 \mathrm{eV}\) por molécula. Quizás contraintuitivamente, este enlace covalente cuántico-mecánico es incluso más fuerte que el enlace clásico (iónico) más fuerte debido a la transferencia de electrones entre átomos, lo que lleva a la atracción Coulomb de los iones resultantes. (Por ejemplo, la cohesión atómica en la\(\mathrm{NaCl}\) molécula es justa\(3.28 \mathrm{eV}\).)

Ahora analicemos las propiedades dinámicas de nuestro sistema modelo (Fig. 19) porque tal par de pozos de potencial débilmente acoplados es nuestro primer ejemplo de la clase muy importante de sistemas de dos niveles. \({ }^{43}\)Es más fácil hacerlo en el límite de acoplamiento débil\(\kappa_{0} a>>1\), cuando los resultados simples (168) - (170) y (174) - (176) son cuantitativamente válidos. En particular, las ecuaciones (169) y (175) nos permiten representar los estados cuasilocalizados de la partícula en cada pozo parcial, así como combinaciones lineales de sus dos estados propios:\[\psi_{\mathrm{R}}(x)=\frac{1}{\sqrt{2}}\left[\psi_{\mathrm{S}}(x)+\psi_{\mathrm{A}}(x)\right], \quad \psi_{\mathrm{L}}(x)=\frac{1}{\sqrt{2}}\left[\psi_{\mathrm{S}}(x)-\psi_{\mathrm{A}}(x)\right] .\] Realicemos el siguiente experimento de pensamiento (“gedanken”): colocar una partícula, en\(t=0\), en uno de estos cuasi- estados localizados, digamos\(\psi_{\mathrm{R}}(x)\), y dejar el sistema solo para evolucionar, de manera que\[\Psi(x, 0)=\psi_{\mathrm{R}}(x)=\frac{1}{\sqrt{2}}\left[\psi_{\mathrm{S}}(x)+\psi_{\mathrm{A}}(x)\right] .\] De acuerdo con la solución general (1.69) de la ecuación de Schrödinger independiente del tiempo, la dinámica de tiempo de esta función de onda puede obtenerse simplemente multiplicando cada función propia por la correspondiente factor tiempo complejo-exponencial:\[\Psi(x, t)=\frac{1}{\sqrt{2}}\left[\psi_{\mathrm{S}}(x) \exp \left\{-i \frac{E_{\mathrm{S}}}{\hbar} t\right\}+\psi_{\mathrm{A}}(x) \exp \left\{-i \frac{E_{\mathrm{A}}}{\hbar} t\right\}\right] .\] A partir de aquí, usando las ecuaciones (170) y (176), y luego las ecuaciones (169) y (175) de nuevo, obtenemos\[\begin{aligned} \Psi(x, t) &=\frac{1}{\sqrt{2}}\left(\psi_{\mathrm{S}}(x) \exp \left\{\frac{i \delta t}{\hbar}\right\}+\psi_{\mathrm{A}}(x) \exp \left\{-\frac{i \delta t}{\hbar}\right\}\right) \exp \left\{-\frac{i E_{0} t}{\hbar}\right\} \\ & \equiv\left(\psi_{\mathrm{R}}(x) \cos \frac{\delta t}{\hbar}+i \psi_{\mathrm{L}}(x) \sin \frac{\delta t}{\hbar}\right) \exp \left\{-i \frac{E_{0} t}{\hbar}\right\} . \end{aligned}\] Este resultado implica, en particular, que las probabilidades\(W_{\mathrm{R}}\) y\(W_{\mathrm{L}}\) encontrar la partícula, respectivamente, en la derecha e izquierda pozos cambian con el tiempo como\[W_{\mathrm{R}}=\cos ^{2} \frac{\delta t}{\hbar}, \quad W_{\mathrm{L}}=\sin ^{2} \frac{\delta t}{\hbar},\] misericordiosamente dejando constante la probabilidad total:\(W_{\mathrm{R}}+W_{\mathrm{L}}=1\). (Si nuestro cálculo no hubiera pasado esta comprobación de cordura, estaríamos en grandes problemas).

Este es el famoso efecto de las oscilaciones cuánticas\(^{44}\) de la función de onda de la partícula entre dos subsistemas similares acoplados, con la frecuencia\[\omega=\frac{2 \delta}{\hbar} \equiv \frac{E_{\mathrm{A}}-E_{\mathrm{S}}}{\hbar} .\] En su última forma, este resultado no depende de la suposición de acoplamiento débil, aunque la forma simple (181) de las oscilaciones, con sus variaciones\(100 \%\) de probabilidad, lo hace. (De hecho, en un fuerte acoplamiento de dos subsistemas, la noción misma de los estados cuasi-localizados\(\psi_{\mathrm{R}}\) y\(\psi_{\mathrm{L}}\) es ambigua.) Cualitativamente, este efecto puede interpretarse de la siguiente manera: la partícula, colocada en uno de los pozos potenciales, intenta escapar de ella a través de túneles a través de la barrera potencial que separa los pozos. (En nuestro sistema particular, mostrado en la Fig. 17, la barrera está formada por el segmento espacial de longitud\(a\), que tiene la energía potencial,\(U=\) 0, mayor que la energía del estado propio)\(-E_{0}\). Sin embargo, en el sistema de dos pocillos, la partícula solo puede escapar al pozo adyacente. Después de la tunelización en ese pozo de contraparte, la partícula intenta escapar de ella, y de ahí regresa, etc. -mucho como un oscilador 1D clásico, inicialmente desviado de su posición de equilibrio, a una amortiguación insignificante.

Se requiere cierta atención en el uso de dicha interpretación para conclusiones cuantitativas. En particular, comparemos el periodo\(\tau \equiv 2 \pi / \omega\) de las oscilaciones (181) con la vida útil del estado metaestable discutido en la sección anterior. Para nuestro modelo particular, podemos usar el segundo de las ecuaciones (170) para escribir\[\omega=\frac{4\left|E_{0}\right|}{\hbar} \exp \left\{-\kappa_{0} a\right\}, \quad \tau=\frac{\pi \hbar}{\delta}=\frac{\pi \hbar}{2\left|E_{0}\right|} \exp \left\{\kappa_{0} a\right\} \equiv \frac{t_{\mathrm{a}}}{2} \exp \left\{\kappa_{0} a\right\}, \quad \text { for } \kappa_{0} a>>1,\] dónde\(t_{\mathrm{a}} \equiv 2 \pi / \omega_{0} \equiv 2 \pi \hbar /\left|E_{0}\right|\) está el tiempo de intento efectivo. Por otro lado, de acuerdo con la Ec. (80), la transparencia\(\mathscr{T}\) de nuestra barrera potencial, en este límite, escala de\(\exp \left\{-2 \kappa_{0} a\right\},{ }^{45}\) manera que de acuerdo a la relación general (153), la vida útil\(\tau\) es del orden de\(t_{\mathrm{a}} \exp \left\{2 \kappa_{0} a\right\} \gg T\). Este es un resultado bastante contradictorio: la velocidad de tunelización de partículas en un pozo adyacente similar es mucho mayor que eso, a través de una barrera similar, ¡al espacio libre! Para demostrar que este importante resultado no es un artefacto de nuestro modelo delta-funcional de la barrera potencial, y también comparar\(\tau\) y\(\tau\) más directamente, analicemos las oscilaciones cuánticas entre dos pozos débilmente acoplados, asumiendo ahora que el (simétrico) perfil potencial\(U(x)\) es suficientemente suave (Fig. 21), de manera que todas sus funciones propias\(\psi_{\mathrm{S}}\) y\(\psi_{\mathrm{A}}\) son al menos diferenciables en todos los puntos. \({ }^{46}\)Si la transparencia de la barrera es baja, las funciones de onda cuasilocalizadas\(\psi_{\mathrm{R}}(x)\) y\(\psi_{\mathrm{L}}(x)=\psi_{\mathrm{R}}(-x)\) y sus energías propias se pueden encontrar aproximadamente resolviendo las ecuaciones de Schrödinger en uno de los pozos, descuidando el túnel a través de la barrera, pero el cálculo de\(\delta\) requiere un poco más de cuidado. Escribamos las ecuaciones estacionarias de Schrödinger para las soluciones simétricas y antisimétricas en la forma\[\left[E_{\mathrm{A}}-U(x)\right] \psi_{\mathrm{A}}=-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{\mathrm{A}}}{d x^{2}}, \quad\left[E_{\mathrm{S}}-U(x)\right] \psi_{\mathrm{S}}=-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{\mathrm{S}}}{d x^{2}},\] multiplicar la primera ecuación por\(\psi_{\mathrm{S}}\) y la segunda por\(\psi_{\mathrm{A}}\), restarlas unas de otras, y luego integrar el resultado de 0 a \(\infty\). El resultado es\[\left(E_{\mathrm{A}}-E_{\mathrm{S}}\right) \int_{0}^{\infty} \psi_{\mathrm{S}} \psi_{\mathrm{A}} d x=\frac{\hbar^{2}}{2 m} \int_{0}^{\infty}\left(\frac{d^{2} \psi_{\mathrm{S}}}{d x^{2}} \psi_{\mathrm{A}}-\frac{d^{2} \psi_{\mathrm{A}}}{d x^{2}} \psi_{\mathrm{S}}\right) d x .\] Si\(U(x)\), y por lo tanto\(d^{2} \psi_{\mathrm{A}, \mathrm{S}} / d x^{2}\), son finitos para todos\(x\), podemos integrar el lado derecho por partes para obtener\[\left(E_{\mathrm{A}}-E_{\mathrm{S}}\right) \int_{0}^{\infty} \psi_{\mathrm{S}} \psi_{\mathrm{A}} d x=\frac{\hbar^{2}}{2 m}\left(\frac{d \psi_{\mathrm{S}}}{d x} \psi_{\mathrm{A}}-\frac{d \psi_{\mathrm{A}}}{d x} \psi_{\mathrm{S}}\right)_{0}^{\infty}\]

Fig. 2.21. Acoplamiento débil entre dos pozos similares de potencial blando.

Hasta el momento, este resultado es exacto (siempre que los derivados que participan en él sean finitos en cada punto); para pozos débilmente acoplados, puede simplificarse aún más. En efecto, en este caso, el lado izquierdo de la Ec. (186) puede aproximarse\[\left(E_{\mathrm{A}}-E_{\mathrm{S}}\right) \int_{0}^{\infty} \psi_{\mathrm{S}} \psi_{\mathrm{A}} d x \approx \frac{E_{\mathrm{A}}-E_{\mathrm{S}}}{2} \equiv \delta,\] ya que esta integral está dominada por la cercanía del punto\(x=a / 2\), donde los segundos términos en cada una de las ecuaciones (169) y (175) son despreciables, y la integral es igual a\(1 / 2\), asumiendo la normalización adecuada de la función\(\psi_{\mathrm{R}}(x)\). En el lado derecho de la Ec. (186), la sustitución en\(x=\infty\) desaparece (debido a la decadencia de la ondulación en la región clásicamente prohibida), y también lo hace el primer término en\(x=0\), porque para la solución antisimétrica,\(\psi_{\mathrm{A}}(0)=0\). Como resultado, la media división de energía\(\delta\) puede expresarse en cualquiera de las siguientes formas (equivalentes):\[\delta=\frac{\hbar^{2}}{2 m} \psi_{\mathrm{S}}(0) \frac{d \psi_{\mathrm{A}}}{d x}(0)=\frac{\hbar^{2}}{m} \psi_{\mathrm{R}}(0) \frac{d \psi_{\mathrm{R}}}{d x}(0)=-\frac{\hbar^{2}}{m} \psi_{\mathrm{L}}(0) \frac{d \psi_{\mathrm{L}}}{d x}(0) .\] Es sencillo (y por lo tanto se deja para el ejercicio del lector) mostrar que dentro de los límites de la validez de la aproximación WKB, la Ec. (188) puede reducirse a\[\delta=\frac{\hbar}{t_{\mathrm{a}}} \exp \left\{-\int_{x_{\mathrm{c}}}^{x_{\mathrm{c}}^{\prime}} \kappa\left(x^{\prime}\right) d x^{\prime}\right\}, \quad \text { so that } \tau \equiv \frac{\pi \hbar}{\delta}=\frac{t_{\mathrm{a}}}{2} \exp \left\{\int_{x_{\mathrm{c}}}^{x_{\mathrm{c}}^{\prime}} \kappa\left(x^{\prime}\right) d x^{\prime}\right\}\] donde \(t_{\mathrm{a}}\)es el periodo de tiempo del movimiento clásico de la partícula, con la energía\(E \approx E_{\mathrm{A}} \approx E_{\mathrm{S}}\), dentro de cada pozo, la función\(\kappa(x)\) se define por la ecuación (82), y\(x_{\mathrm{c}}\) y\(x_{\mathrm{c}}\) 'son los puntos de inflexión clásicos limitantes la barrera potencial a nivel\(E\) de la energía propia de la partícula - ver Fig. 21. El resultado (189) es evidentemente una generalización natural de la ecuación (183), de manera que la fuerte relación entre los tiempos de tunelización de partículas en el continuo de estados y en un autoestado discreto, en efecto no es específica para el modelo delta-funcional. Volveremos a este hecho, en su forma más general, al final del Capítulo 6.

---

\({ }^{38}\)Ver Ecuaciones. (56) - (58), con\(U_{0}=0\).

\({ }^{39}\)Tales ecuaciones algebraicas para ecuaciones diferenciales lineales se denominan frecuentemente características.

\({ }^{40}\)Obsérvese que esto\(E_{0}\) es igual, por magnitud, a la constante\(E_{0}\) que participa en la Ec. (79). Obsérvese también que este resultado en realidad ya se obtuvo, “hacia atrás”, en la solución del Problema 1.12 (ii), pero esa solución no abordó la cuestión de si el potencial calculado (158) podría sostener otros autoestados localizados.

\({ }^{41}\)Históricamente, el desarrollo de la teoría cuántica de tal unión en la\(\mathrm{H}_{2}\) molécula (por Walter Heinrich Heitler y Fritz Wolfgang Londres en 1927) fue el avance decisivo para la aceptación de la mecánica cuántica emergente por parte de la comunidad de químicos.

\({ }^{42}\)Debido a los espines opuestos de estos electrones, el principio Pauli les permite estar en el mismo estado basal orbital - ver Capítulo 8.

\({ }^{43}\)Como veremos más adelante en el Capítulo 4, estas propiedades son similares a las de las\(1 / 2\) partículas de espín; de ahí que los sistemas de dos niveles se denominan frecuentemente los sistemas de tipo spin-1/2.

\({ }^{44}\)A veces se les llama las oscilaciones Bloch, pero más comúnmente el último término se reserva para un efecto relacionado pero diferente en sistemas espacialmente periódicos, que se discutirá en la Sec. 8 a continuación.

\({ }^{45}\)Es difícil usar la Eq. (80) para una evaluación más exacta de\(\mathscr{T}\) en nuestro sistema actual, con sus pozos potenciales infinitamente profundos, porque el significado del número de onda no\(k\) está del todo claro. Sin embargo, esto no es demasiado importante, porque en el límite\(\kappa_{0} a \gg 1\), el exponente de tunelización hace la contribución dominante a la transparencia ver, nuevamente, Fig. 2.7b.

\({ }^{46}\)Un pozo tan suave puede tener más de un estado propio cuasi-localizado, de manera que el índice de estado (y energía) apropiado\(n\) está implícito en todas las fórmulas restantes de esta sección.