2.8: Sistemas periódicos: bandas de energía y brechas

Pasemos ahora a la discusión de uno de los temas más importantes de la mecánica de las olas: el movimiento de partículas a través de un sistema periódico. Como precursor de esta discusión, calculemos la transparencia del perfil potencial mostrado en la Fig. 22 (frecuentemente llamado\(\operatorname{Dirac}\) peine): una secuencia de barreras\(N\) similares equidistantes de potencial delta funcionales, separadas por barreras\((N-1)\) libres de potencial intervalos\(a\).

Fig. 2.22. Túneles a través de un peine Dirac: un sistema de barreras\(N\) similares equidistantes, es decir, pozos potenciales acoplados\((N-1)\) similares.

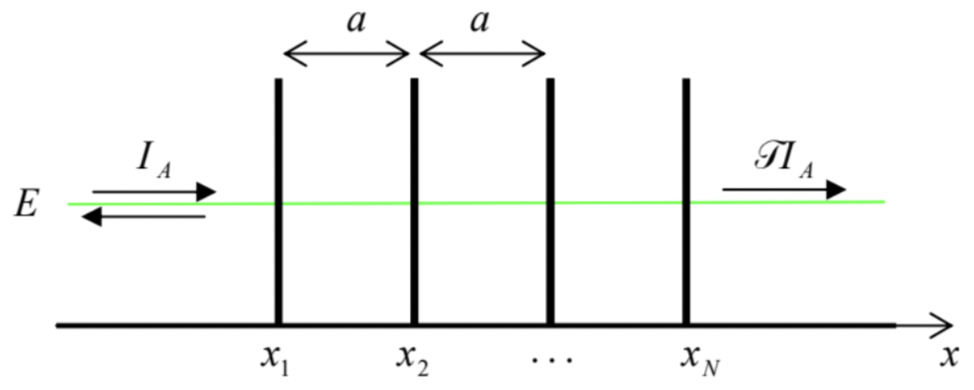
De acuerdo con la Ec. (132), su matriz de transferencia es el siguiente producto\[\mathrm{T}=\underbrace{\mathrm{T}_{\alpha} \mathrm{T}_{a} \mathrm{~T}_{\alpha} \ldots \mathrm{T}_{a} \mathrm{~T}_{\alpha}}_{(N-1)+N \text { terms }},\] con las matrices de componentes dadas por las ecuaciones (135) y (138), y el parámetro de altura de barrera\(\alpha\) definido por la última de las ecuaciones (78). Sorprendentemente, esta multiplicación se puede llevar a cabo analíticamente,\({ }^{47}\) dando\[\mathscr{T} \equiv\left|T_{11}\right|^{-2}=\left[(\cos N q a)^{2}+\left(\frac{\sin k a-\alpha \cos k a}{\sin q a} \sin N q a\right)^{2}\right]^{-1},\] donde\(q\) se encuentra un nuevo parámetro, con la dimensionalidad del número de onda, definida por la siguiente relación:\[\cos q a \equiv \cos k a+\alpha \sin k a .\] For\(N=1\), Eqs. (191) inmediatamente rendimiento nuestro viejo resultado (79), mientras\(N=2\) que para ellos pueden reducirse fácilmente a la Ec. (141) - ver Fig. 16a. La Fig. 20 muestra sus predicciones para dos números mayores\(N\), y varios valores del parámetro adimensional\(\alpha\).

Comencemos la discusión de las parcelas a partir del caso\(N=3\), cuando tres barreras limitan dos pozos potenciales acoplados entre ellas. La comparación de la Fig. 23a y la Fig. 16a muestra que los patrones de transmisión, y su dependencia del parámetro\(\alpha\), son muy similares, además de que en el sistema de pozo acoplado, cada pico de tunelización resonante se divide en dos, con la\(k a\) diferencia -entre ellos escalando como \(1 / \alpha\). De la discusión en la última sección, ahora podemos interpretar fácilmente este resultado: cada par de picos de resonancia de transparencia corresponde a la alineación de la energía de la partícula incidente\(E\) con el par de niveles de energía\(E_{\mathrm{A}}, E_{\mathrm{S}}\) de los estados simétrico y antisimétrico del sistema. Sin embargo, en contraste con el sistema mostrado en la Fig. 19, estos estados son metaestables, debido a que la partícula puede escaparse de estos estados tal como podría hacerlo en el sistema estudiado en la Sec. 5 - ver Fig. 15 y su discusión. Como resultado, cada uno de los picos resonantes tiene un ancho de energía distinto de cero\(\Delta E\), obedeciendo a la Ec. (155).

Fig. 2.23. La transparencia del peine Dirac en función del producto\(k a\) para tres valores de\(\alpha\). Dado que la función\(\mathscr{T} k a\)) es\(\pi\) -periódica (igual que lo es para\(N=2\), ver Fig. 16a), sólo se muestra un periodo.

Un aumento adicional de\(N\) (ver Fig. 23b) da como resultado el aumento del número de picos resonantes por período a\((N-1)\), y en\(N \rightarrow \infty\) los picos se funden en las llamadas bandas de energía permitidas (frecuentemente llamadas solo las “bandas de energía”) con transparencia promedio \(\mathscr{T} \sim 1\), separados de bandas similares en los periodos adyacentes de función\(\mathcal{T}(\mathrm{ka})\) por brechas de energía\(^{48}\) donde\(\mathcal{T} \rightarrow 0\). Observe las siguientes características importantes del patrón:

(i) en\(N \rightarrow \infty\), los bordes de la banda/brecha se vuelven afilados para cualquier\(\alpha\), y tienden a posiciones fijas (determinadas por\(\alpha\) pero independientes de\(N\));

(ii) cuanto más grande es el acoplamiento de pozo (cuanto menor es\(\alpha\)), más amplias son las bandas de energía permitidas y cuanto más estrechas son las brechas entre ellas.

Nuestra discusión previa sobre el túnel resonante nos da una pista para una interpretación semicuantitativa de este patrón: si los pozos\((N-1)\) potenciales se acoplan débilmente mediante túneles a través de las barreras potenciales que los separan, el espectro de energía del sistema consiste en grupos de \((N-1)\)niveles de energía metaestables, estando cada grupo cerca de una de las energías propias imperturbables del pozo. (De acuerdo con la Ec. (1.84), para nuestro ejemplo actual mostrado en la Fig. 22, con sus pozos de potencial rectangulares, estas energías propias corresponden a\(k_{n} a=\pi n\).)

Ahora recordemos que en el caso\(N=2\), analizado en el apartado anterior, las funciones propias (169) y (175) diferían sólo por el desplazamiento de fase\(\Delta \varphi\) entre sus componentes localizados\(\psi_{\mathrm{R}}(x)\) y\(\psi_{\mathrm{L}}(x)\), con\(\Delta \varphi=0\) para uno de ellos\((\psi \mathrm{s})\) y\(\Delta \varphi=\pi\) para su contraparte. De ahí que sea natural esperar que para otros\(N\) también, cada nivel de energía metaestable corresponda a una función propia que es una superposición de funciones localizadas similares en cada pozo potencial, pero con ciertos cambios de fase\(\Delta \varphi\) entre ellas.

Además, podemos esperar que en\(N \rightarrow \infty\), es decir, para estructuras periódicas\({ }^{49}\) con\[U(x+a)=U(x),\] cuando el sistema no tiene los extremos que podrían afectar sus propiedades, los desplazamientos de fase\(\Delta \varphi\) entre las funciones de onda localizadas en todas las parejas de potencial adyacente pozos deben ser iguales, es decir,\[\psi(x+a)=\psi(x) e^{i \Delta \varphi}\] para todos\(x .{ }^{50}\) Esta igualdad es la (versión 1D del) tan célebre teorema de Bloch. \({ }^{51}\)El rigor matemático a un lado,\({ }^{52}\) es un hecho prácticamente evidente porque la densidad de la partícula\(w(x)=\psi^{*}(x) \psi(x)\), que tiene que ser periódica en este sistema\(a\) -periódico, puede ser así solo\(\Delta \varphi\) es constante. Para lo que sigue, es más conveniente representar la constante real\(\Delta \varphi\) en la forma\(q a\), de manera que el teorema de Bloch tome la forma\[\psi(x+a)=\psi(x) e^{i q a} .\] El sentido físico del parámetro se\(q\) discutirá en detalle a continuación, pero podemos inmediatamente observe que de acuerdo con la Ec. (193b), una adición de\((2 \pi / a)\) a este parámetro produce la misma función de onda; por lo tanto, todos los observables tienen que ser funciones\((2 \pi / a)\) -periódicas de\(q .{ }^{53}\)

Ahora usemos el teorema de Bloch para calcular las funciones propias y las energías propias para la versión infinita del sistema que se muestra en la Fig. 22, es decir, para un conjunto infinito de barreras potenciales delta-funcionales - ver Fig. \(24 .\)

Fig. 2.24. El potencial periódico más simple: un peine Dirac infinito.

Para comenzar, consideremos dos puntos separados por un periodo\(a\): uno de ellos,\(x_{j}\), justo a la izquierda de la posición de una de las barreras, y otro,\(x_{j+1}\), justo a la izquierda de la siguiente barrera-ver nuevamente la Fig. 24. Las funciones propias en cada uno de los puntos pueden representarse como superposiciones lineales de dos ondas simples\(\exp \{\pm i k x\}\), y las amplitudes de sus componentes deben estar relacionadas por una matriz\(\mathrm{T}\) de\(2 \times 2\) transferencia del fragmento potencial que las separa. De acuerdo con la Ec. (132), esta matriz se puede encontrar como el producto de la matriz (135) de una barrera delta-funcional por la matriz (138) de un intervalo de potencial cero\(a\):\[\left(\begin{array}{l} A_{j+1} \\ B_{j+1} \end{array}\right)=\mathrm{T}_{\mathbf{a}} \mathrm{T}_{\alpha}\left(\begin{array}{l} A_{j} \\ B_{j} \end{array}\right)=\left(\begin{array}{cc} e^{i k a} & 0 \\ 0 & e^{-i k a} \end{array}\right)\left(\begin{array}{cc} 1-i \alpha & -i \alpha \\ i \alpha & 1+i \alpha \end{array}\right)\left(\begin{array}{l} A_{j} \\ B_{j} \end{array}\right) .\] Sin embargo, según el teorema de Bloch (193b), las amplitudes de los componentes también deben estar relacionadas como \[\left(\begin{array}{l} A_{j+1} \\ B_{j+1} \end{array}\right)=e^{i q a}\left(\begin{array}{l} A_{j} \\ B_{j} \end{array}\right) \equiv\left(\begin{array}{cc} e^{i q a} & 0 \\ 0 & e^{i q a} \end{array}\right)\left(\begin{array}{l} A_{j} \\ B_{j} \end{array}\right) .\]La condición de autoconsistencia de estas dos ecuaciones da la siguiente ecuación característica:\[\left|\left(\begin{array}{cc} e^{i k a} & 0 \\ 0 & e^{-i k a} \end{array}\right)\left(\begin{array}{cc} 1-i \alpha & -i \alpha \\ i \alpha & 1+i \alpha \end{array}\right)-\left(\begin{array}{cc} e^{i q a} & 0 \\ 0 & e^{i q a} \end{array}\right)\right|=0 .\] En la Sec. 5, ya hemos calculado el producto matricial que participa en esta ecuación - ver el segundo operando en la Ec. (140). Al usarlo, vemos que la Eq. (196) se reduce a la misma ecuación simple (191b) que nos ha saltado de la solución del problema algo diferente (tunelización resonante). Exploremos ese simple resultado en detalle. En primer lugar, el lado izquierdo de la Ec. (191b) es una función sinusoidal del producto\(q a\) con amplitud unitaria, mientras que su lado derecho es una función sinusoidal del producto\(k a\), con amplitud\(\left(1+\alpha^{2}\right)^{1 / 2}>1\) - ver Fig. 25,

Fig. 2.25. La representación gráfica de la ecuación característica (191b) para un valor fijo del parámetro\(\alpha\). Los rangos de\(k a\) ese rendimiento\(|\cos q a|<1\), corresponden a bandas de energía permitidas, mientras que aquellos con\(|\cos q a|>1\), corresponden a brechas de energía entre ellas.

Como resultado, dentro de cada medio periodo\(\Delta(k a)=\pi\) del lado derecho, existe un intervalo donde la magnitud del lado derecho es mayor que 1, de manera que la ecuación característica no tiene una solución real para\(q\). Estos intervalos corresponden a los huecos de energía (ver Fig. 23 nuevamente), mientras que los intervalos complementarios de\(k a\), donde\(q\) existe una solución real para, corresponden a las bandas de energía permitidas. En contraste, el parámetro\(q\) puede tomar cualquier valor real, por lo que es más conveniente trazar la energía\(E=\hbar^{2} k^{2} / 2 m\) propia como función del cuasimomentum\(\hbar q\) (o, aún más convenientemente, del parámetro adimensional\(q a\)) más bien que\(k a .^{54}\) Antes de hacer eso, debemos recordar que el parámetro\(\alpha\), definido por la última de las ecuaciones (78), también depende del vector\(k\) de onda, de modo que si variamos\(q\) (y por lo tanto\(k\)), es mejor caracterizar la estructura por otro parámetro adimensional\(k\) independiente, por ejemplo para\[\beta \equiv(k a) \alpha \equiv \frac{w}{\hbar^{2} / m a},\] que nuestra ecuación característica (191b) se convierta en la\[\cos q a \equiv \cos k a+\beta \frac{\sin k a}{k a} .\] Fig. 26 muestra las gráficas de\(k\) y\(E\), siguiendo de la Ec. (198), como funciones de\(q a\), para un valor particular, moderado del parámetro\(\beta\). La primera característica evidente del patrón es la\(2 \pi\) -periodicidad del patrón en el argumento\(q a\), que ya hemos predicho a partir de los argumentos generales del teorema de Bloch. (Debido a esta periodicidad, se puede estudiar el patrón completo de banda/brecha, por ejemplo, en un solo intervalo\(-\pi \leq q a \leq+\pi\), llamado zona\(1^{\text {st }}\) Brillouin, la llamada imagen de zona reducida. Para algunas aplicaciones, sin embargo, es más conveniente usar la imagen de zona extendida con\(-\infty \leq q a \leq+\infty-\) ver, por ejemplo, la siguiente sección.)

Fig. 2.26. (a) El impulso “genuino”\(k\) de una partícula en un peine Dirac infinito (Fig. 24), y (b) su energía\(E=\hbar^{2} k^{2} / 2 m\) (en las unidades de\(E_{0} \equiv \hbar^{2} / 2 m a^{2}\)), como funciones de cuasimomentum normalizado, para un valor particular\((\beta=3)\) del parámetro adimensional definido por la Ec. (197). Las flechas en la esquina inferior derecha del panel (b) ilustran la definición de\(\left(\Delta_{n}\right)\) ancho de banda de energía\(\left(\Delta E_{n}\right)\) y brecha de energía.

Sin embargo, quizás el hecho más importante, claramente visible en la Fig. 26, es que hay un número infinito de bandas de energía, con diferentes energías\(E_{n}(q)\) para el mismo valor de\(q\). Matemáticamente, es evidente a partir de la Ec. (198) - o alternativamente de la Fig. 25. En efecto, para cada valor de\(q a\), hay una solución\(k a\) a esta ecuación en cada medio periodo\(\Delta(k a)=\pi\). Cada una de esas soluciones (ver Fig. 26a) da un valor específico de la energía de las partículas\(E=\hbar^{2} k^{2} / 2 m\). Un conjunto continuo de soluciones similares para diversas\(q a\) formas de una banda de energía particular.

Dado que la imagen de la banda de energía es uno de los resultados prácticamente más importantes de la mecánica cuántica, es imperativo comprender su física. Es natural describir esta física de dos maneras diferentes en dos límites de fuerza potencial opuestos. Paralelamente, utilizaremos esta discusión para obtener expresiones más simples para la estructura de banda/brecha de energía en cada límite. Una ventaja importante de este enfoque es que ambos análisis pueden realizarse para un potencial periódico arbitrario y\(U(x)\) no para el modelo particular mostrado en la Fig. 24.

i) Aproximación de unión estrecha. Esta aproximación funciona bien cuando la energía propia\(E_{n}\) de los estados cuasilocalizados en los mínimos del perfil energético es mucho menor que la altura de las barreras potenciales que los separan - ver Fig. 27. Como debería quedar claro a partir de nuestra discusión en la Sec. 6, esencialmente el único papel del acoplamiento entre estos estados (a través de túneles a través de las barreras potenciales que separan los mínimos) es establecer un cierto desplazamiento de fase\(\Delta \varphi \equiv q a\) entre las funciones de onda cuasilocalizadas adyacentes\(u_{n}\left(x-x_{j}\right)\) y\(u_{n}\left(x-x_{j+1}\right)\).

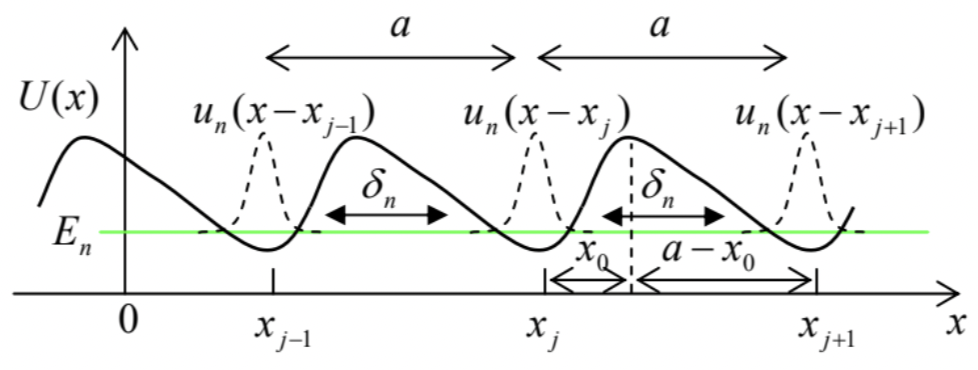Fig. 2. 27. La aproximación de unión estrecha (esquemáticamente).

Para describir este efecto cuantitativamente, volvamos primero al problema de dos pozos acoplados considerados en la Sec. 6, y refundir el resultado\((180)\), con índice de autoestado restaurado\(n\), como\[\Psi_{n}(x, t)=\left[a_{\mathrm{R}}(t) \psi_{\mathrm{R}}(x)+a_{\mathrm{L}}(t) \psi_{\mathrm{L}}(x)\right] \exp \left\{-i \frac{E_{n}}{\hbar} t\right\},\] donde las amplitudes de probabilidad\(a_{\mathrm{R}}\) y \(a_{\mathrm{L}}\)oscilar sinusoidalmente en el tiempo:\[a_{\mathrm{R}}(t)=\cos \frac{\delta_{n}}{\hbar} t, \quad a_{\mathrm{L}}(t)=i \sin \frac{\delta_{n}}{\hbar} t .\] Esta evolución satisface el siguiente sistema de dos ecuaciones cuya estructura es similar a la Ec. (1.61a): La\[i \hbar \dot{a}_{\mathrm{R}}=-\delta_{n} a_{\mathrm{L}}, \quad i \hbar \dot{a}_{\mathrm{L}}=-\delta_{n} a_{\mathrm{R}} .\] ecuación (199) puede generalizarse fácilmente al caso de muchos pozos acoplados similares:\[\Psi_{n}(x, t)=\left[\sum_{j} a_{j}(t) u_{n}\left(x-x_{j}\right)\right] \exp \left\{-i \frac{E_{n}}{\hbar} t\right\},\] ¿dónde\(E_{n}\) están los energías propias y\(u_{n}\) las funciones propias de cada pozo. En el límite de unión estrecha, solo se acoplan los pozos adyacentes, de manera que en lugar de la ecuación (201) debemos escribir un sistema infinito de ecuaciones similares\[i \hbar \dot{a}_{j}=-\delta_{n} a_{j-1}-\delta_{n} a_{j+1},\] para cada número de pozo\(j\), donde los parámetros\(\delta_{n}\) describen el acoplamiento entre dos pozos potenciales adyacentes. Repitiendo el cálculo esbozado al final de la última sección para nuestra nueva situación, para un potencial suave podemos obtener una expresión esencialmente similar a la última forma de la ecuación (188):\[\delta_{n}=\frac{\hbar^{2}}{m} u_{n}\left(x_{0}\right) \frac{d u_{n}}{d x}\left(a-x_{0}\right)\] donde\(x_{0}\) está la distancia entre el fondo del pozo y el medio de la barrera potencial a la derecha del mismo - ver Fig. 27. La única característica sustancial nueva de esta expresión en comparación con la ecuación (188) es que el signo de\(\delta_{n}\) alterna con el número de nivel\(n: \delta_{1}>0, \delta_{2}<0, \delta_{3}>0\), etc. De hecho, el número de ceros (y por lo tanto, “menea”) de las funciones propias\(u_{n}(x)\) de cualquier pozo potencial aumenta como se\(n-\) ve, por ejemplo, la Fig. \(1.8{ }^{55}\)de manera que la diferencia de las colas exponenciales de las funciones, escabullirse bajo las barreras izquierda y derecha limitando el pozo también alterna con\(n\).

El sistema infinito de ecuaciones diferenciales ordinarias (203) permite resolver muchos problemas importantes (como la propagación de la función ondulada que inicialmente se localizó en un pozo, etc.), pero nuestra tarea en este momento es solo encontrar sus estados estacionarios, es decir, las soluciones proporcionales a \(\exp \left\{-i\left(\varepsilon_{n} / \hbar\right) t\right\}\), donde\(\varepsilon_{n}\) es una suma aún desconocida,\(q\) dependiente de la energía\(E_{n}\) de fondo del nivel de\(n^{\text {th }}\) energía. Para satisfacer también el teorema de Bloch (193), tal solución debe tener la siguiente forma:\[a_{j}(t)=a \exp \left\{i q x_{j}-i \frac{\varepsilon_{n}}{\hbar} t+\text { const }\right\} .\] Conectando esta solución a la ecuación (203) y cancelando el exponente común, obtenemos de\[E=E_{n}+\varepsilon_{n}=E_{n}-\delta_{n}\left(e^{-i q a}+e^{i q a}\right) \equiv E_{n}-2 \delta_{n} \cos q a\] manera que en esta aproximación, el ancho de banda de energía\(\Delta E_{n}\) (ver Fig. 26b) es igual a \(4\left|\delta_{n}\right|\).

La relación (206), cuya validez está restringida\(\left|\delta_{n}\right|<<E_{n}\), describe razonablemente bien las bandas de energía más bajas trazadas en la Fig. 26b. (Para mayores\(\beta\), el acuerdo sería aún mejor.) Entonces, este cálculo explica cuáles son realmente las bandas de energía: en el límite de unión estrecha se interpretan mejor como niveles de energía de pozos aislados\(E_{n}\), ampliados en bandas por la interacción interwell. Además, este resultado da una clara prueba de que los extremos de la banda de energía corresponden a\(q a=2 \pi l\) y\(q a=2 \pi(l+1 / 2)\), con entero l. Finalmente, la alteración del signo del coeficiente de acoplamiento\(\delta_{n}(204)\) explica por qué se alinean los máximos de energía de una banda, en el \(q a\)eje, con mínimos de energía de las bandas adyacentes - ver Fig. 26.

ii) Límite de potencial débil. Sorprendentemente, la estructura de banda de energía también es compatible con una imagen física completamente diferente que puede desarrollarse en el límite opuesto. Que la energía de la partícula\(E\) sea tan alta que el potencial periódico\(U(x)\) pueda ser tratado como una pequeña perturbación. Ingenuamente, en este límite podríamos esperar una relación de dispersión parabólica ligeramente y suavemente deformada\(E=\hbar^{2} k^{2} / 2 m\). Sin embargo, si estamos trazando la energía del estado estacionario como una función de más\(q\) bien que\(k\), necesitamos agregar\(2 \pi l / a\), con un entero arbitrario\(l\), al argumento. Demostremos esto expandiendo todas las variables a la serie 1D-espacial de Fourier. Para la energía potencial\(U(x)\) que obedece a la Ec. (192), tal expansión es sencilla: 56\[U(x)=\sum_{l^{\prime \prime}} U_{l^{\prime}} \exp \left\{-i \frac{2 \pi x}{a} l^{\prime \prime}\right\}\] donde la suma es sobre todos los enteros\(l\) “, de\(-\infty\) a\(+\infty\). Sin embargo, para la función de onda debemos mostrar el debido respeto al teorema de Bloch (193), que demuestra que estrictamente hablando, no\(\psi(x)\) es periódico.

Para superar esta dificultad, definamos otra función:\[u(x) \equiv \psi(x) e^{-i q x},\] y estudiemos su periodicidad:\[u(x+a)=\psi(x+a) e^{-i q(x+a)}=\psi(x) e^{-i q x}=u(x)\] Vemos que la nueva función es\(a\) -periódica, y de ahí podemos usar las ecuaciones (208) - (209) para reescribir el teorema de Bloch de una forma diferente:\[\psi(x)=u(x) e^{i q x}, \text { with } u(x+a)=u(x) .\] Ahora es seguro expandir el función periódica\(u(x)\) exactamente como\(U(x)\): de\[u(x)=\sum_{l^{\prime}} u_{l} \exp \left\{-i \frac{2 \pi x}{a} l^{\prime}\right\},\] manera que, según la Eq. (210),\[\psi(x)=e^{i q x} \sum_{l^{\prime}} u_{l^{\prime}} \exp \left\{-i \frac{2 \pi x}{a} l^{\prime}\right\}=\sum_{l^{\prime}} u_{l^{\prime}} \exp \left\{i\left(q-\frac{2 \pi}{a} l^{\prime}\right) x\right\} .\] La única parte no trivial de enchufar las ecuaciones (207) y (212) en la ecuación estacionaria de Schrödinger (53) es cómo manejar el término del producto,\[U(x) \psi=\sum_{l^{\prime}, l^{\prime \prime}} U_{l^{\prime} u} u_{l^{\prime}} \exp \left\{\left[i\left[q-\frac{2 \pi}{a}\left(l^{\prime}+l^{\prime \prime}\right)\right] x\right\} .\right.\] At fijo \(l^{\prime}\), podemos cambiar la suma sobre\(l\) "a eso sobre\(l \equiv l^{\prime}+l^{\prime \prime}\) (para que\(l^{\prime \prime} \equiv l-l^{\prime}\)), y escriba:\[U(x) \psi=\sum_{l} \exp \left\{i\left(q-\frac{2 \pi}{a} l\right) x\right\} \sum_{l^{\prime}} u_{l^{\prime}} U_{l-l^{\prime}} .\] Ahora conectando la Ec. (212) (con el índice de suma\(l\) 'reemplazado por\(l\)) y la Ec. (214) en la ecuación estacionaria de Schrödinger (53), y requiriendo que los coeficientes de cada exponente espacial coincidan, obtenemos un sistema infinito de ecuaciones lineales para\(u_{l}\):

\[\sum_{l^{\prime}} U_{l-l^{\prime}} u_{l^{\prime}}=\left[E-\frac{\hbar^{2}}{2 m}\left(q-\frac{2 \pi}{a} l\right)^{2}\right] u_{l} .\](Obsérvese que mediante este cálculo hemos demostrado esencialmente que la función de onda Bloch (210) es de hecho la\(a\) solución de la ecuación de Schrödinger, siempre que el cuasimomentum\(q\) se seleccione de manera que el sistema de ecuación lineal (215) sea compatible, i.e. es una solución de su ecuación característica.)

Hasta el momento, el sistema de ecuaciones (215) es una alternativa equivalente a la ecuación inicial de Schrödinger, para la fuerza de cualquier potencial. \({ }^{57}\)En el límite de potencial débil, es decir, si todos los coeficientes de Fourier\(U_{n}\) son pequeños\({ }^{58}\) podemos completar todos los cálculos analíticamente. \({ }^{59}\)En efecto, en la llamada\(0^{\text {th }}\) aproximación podemos ignorar todos\(U_{n}\), de manera que para tener al menos uno\(u_{l}\) diferente de 0, la Ec. (215) requiere que\[E \rightarrow E_{l} \equiv \frac{\hbar^{2}}{2 m}\left(q-\frac{2 \pi l}{a}\right)^{2} .\] (\(u_{l}\)sí mismo se obtenga de la condición de normalización). Este resultado significa que en esta aproximación, la relación de dispersión\(E(q)\) tiene un número infinito de ramas cuadráticas similares numeradas por entero\(l\) - ver Fig. 28.

Fig. 2.28. El cuadro de banda/brecha energética en el límite de potencial débil\(\left(\Delta_{n}\right.\)\(<<E^{(n)}\)), con el sombreado mostrando la zona\(1^{\text {st }}\) Brillouin.

En cada rama, dicha función propia tiene solo un coeficiente de Fourier, es decir, es una onda viajera monocromática\[\psi_{l} \rightarrow u_{l} e^{i k x}=u_{l} \exp \left\{i\left(q-\frac{2 \pi l}{a}\right) x\right\} .\] A continuación, la definición anterior de nos\(E_{l}\) permite reescribir la Eq. (215) en una forma más transparente\[\sum_{l^{\prime} \neq l} U_{l-l^{\prime}} u_{l^{\prime}}=\left(E-E_{l}\right) u_{l},\] que puede resolverse formalmente para\(u_{l}\): \[u_{l}=\frac{1}{E-E_{l}} \sum_{l^{\prime} \neq l} U_{l-l^{\prime}} u_{l^{\prime}}\]Esta fórmula muestra que si los coeficientes de Fourier\(U_{n}\) son distintos de cero pero pequeños, las ondas sí adquieren otros componentes de Fourier (además del principal, con el índice correspondiente al número de rama), pero estas adiciones son todas pequeñas, además de regiones estrechas cercanas a los puntos \(E_{l}=E_{l}\), donde dos ramas (216) de la relación de dispersión\(E(q)\), con algunos números específicos\(l\) y\(l^{\prime}\), cruzan. De acuerdo con la Ec. (216), esto sucede cuando\[\left(q-\frac{2 \pi}{a} l\right) \approx-\left(q-\frac{2 \pi}{a} l^{\prime}\right),\] es decir, at\(q \approx q_{m} \equiv \pi m / a\) (con el entero\(m \equiv l+l^{\prime}\))\({ }^{60}\) correspondiente a\[E_{l} \approx E_{l} \approx \frac{\hbar^{2}}{2 m a^{2}}\left[\pi\left(l+l^{\prime}\right)-2 \pi l\right]^{2}=\frac{\pi^{2} \hbar^{2}}{2 m a^{2}} n^{2} \equiv E^{(n)},\] con entero\(n \equiv l-l^{\prime}\). (Según sus definiciones, el índice\(n\) es solo el número del cruce de ramas en la escala de energía, mientras que el índice\(m\) numera la posición de los puntos de cruce en el\(q\) eje -ver Fig. 28.) En tal región,\(E\) tiene que estar cerca de ambos\(E_{l}\) y\(E_{l}\), de manera que el denominador en sólo uno del número infinito de términos en la ecuación (219) es muy pequeño, haciendo que el término sea sustancial a pesar de la pequeñez de\(U_{n}\). De ahí que podamos tener en cuenta solo un término en cada una de las sumas (escritas para\(l\) y\(l^{\prime}\)):\[\begin{aligned} &U_{n} u_{l^{\prime}}=\left(E-E_{l}\right) u_{l}, \\ &U_{-n} u_{l}=\left(E-E_{l^{\prime}}\right) u_{l^{\prime}} . \end{aligned}\] Teniendo en cuenta que para cualquier función real\(U(x)\), los coeficientes de Fourier en su expansión de Fourier (207) tienen que relacionarse como \(U_{-n}=U_{n}{ }^{*}\), la Ec. (222) produce la siguiente ecuación característica simple\[\left|\begin{array}{cc} E-E_{l} & -U_{n} \\ -U_{n}^{*} & E-E_{l^{\prime}} \end{array}\right|=0,\] con la siguiente solución:\[E_{\pm}=E_{\text {ave }} \pm\left[\left(\frac{E_{l}-E_{l}}{2}\right)^{2}+U_{n} U_{n}^{*}\right]^{1 / 2}, \quad \text { with } E_{\text {ave }} \equiv \frac{E_{l}+E_{l^{\prime}}}{2}=E^{(n)}\] De acuerdo con la Ec. (216), cerca del punto de cruce de ramificación\(q_{m}=\pi\left(l+l^{\prime}\right) / a\), la fracción que participa en este resultado puede aproximarse como \({ }^{61}\)\[\frac{E_{l}-E_{l^{\prime}}}{2} \approx \gamma \widetilde{q}, \quad \text { with }\left.\gamma \equiv \frac{d E_{l}}{d q}\right|_{q=q_{m}}=\frac{\pi \hbar^{2} n}{m a}=\frac{2 a E^{(n)}}{\pi n}, \quad \text { and } \widetilde{q} \equiv q-q_{m},\]mientras que los parámetros\(E_{\text {ave }}=E^{(n)}\) y\(U_{n} U_{n}{ }^{*}=\left|U_{n}\right|^{2}\) no dependen de\(\widetilde{q}\), es decir, de la distancia desde el punto central\(q_{m}\). Es por ello que la ecuación (224) se puede trazar como el famoso diagrama anticrosante de nivel (también llamado “cruce evitado”, o “cruce previsto”, o “no cruce”) (Fig. 29), con el ancho de brecha de energía\(\Delta_{n}\) igual a\(2\left|U_{n}\right|\), es decir, solo el doble de la magnitud del \(n\)-ésimo armónico de Fourier del potencial periódico\(U(x)\). Dichos anticrosamientos también son claramente visibles en la Fig. 28, que muestra el resultado de la solución exacta de la Ec. (198) para el caso particular\(\beta=0.5 .62\)

Fig. 2.29. El diagrama anticrosante de niveles.

Nos encontraremos con el diagrama anticrosante una y otra vez en el curso, notablemente en la discusión de sistemas de giro\(-\frac{2}{2}\) y otros sistemas de dos niveles. También se cumple repetidamente en la mecánica clásica, por ejemplo en el cálculo de frecuencias de osciladores acoplados. \({ }^{63} \cdot 64{ }^{4}\)En nuestro caso actual del límite de potencial débil de la teoría de bandas, el diagrama describe la interacción de dos ondas viajeras de Broglie (217), con vectores de onda dirigidos opuestamente,\(l\) y\(-l^{\prime}\), a través de la\(\left(l-l^{\prime}\right)^{\text {th }}\) (es decir, \(n^{\text {th }}\)) Armónico de Fourier del perfil potencial\(U(x){ }^{65}\) Este efecto existe también en la teoría clásica de ondas y se conoce como la reflexión de Bragg, describiendo, por ejemplo, el modelo 1D de la reflexión de la onda X por una red cristalina (véase, por ejemplo, la Fig. 1.5) en el límite de débil interacción entre la onda incidente y cada átomo.

El diagrama anticrosante muestra que de manera bastante contraintuitiva, incluso un potencial periódico débil cambia radicalmente la topología de la relación de dispersión inicialmente parabólica, conectando sus diferentes ramas, y creando así las brechas de energía. Permítanme esperar que el lector haya disfrutado de la elegante descripción de este efecto, comentado anteriormente, así como de una ilustración más de la maravillosa capacidad de la física para dar interpretaciones completamente diferentes (y diferentes enfoques aproximados) al mismo efecto en límites opuestos.

Entonces, hemos explicado analíticamente (aunque sólo en dos límites) la estructura de banda particular mostrada en la Fig. 26. Ahora podemos preguntarnos qué tan general es esta estructura, es decir, cuánto de ella es independiente del modelo de peine Dirac (Fig. 24). Para ello, representemos el patrón de bandas, como el que se muestra en la Fig. \(26 \mathrm{~b}\)(trazado para un valor particular del parámetro\(\beta\), caracterizando la resistencia potencial de barrera) en una forma más condensada, lo que nos permitiría colocar los resultados para un rango de\(\beta\) valores en una sola parcela comprensible. La forma de hacerlo debería quedar clara a partir de la Fig. 26b: dado que la dependencia de la energía del cuasimomentum en cada banda de energía no es demasiado agitada, podemos trazar solo los valores más altos y más pequeños de la energía de la partícula\(E=\hbar^{2} k^{2} / 2 m\) como funciones de\(\beta \equiv\) maw/ \(\hbar^{2}\)- ver Fig. 30, que puede obtenerse de la Ec. (198) con\(q a=0\) y\(q a=\pi\).

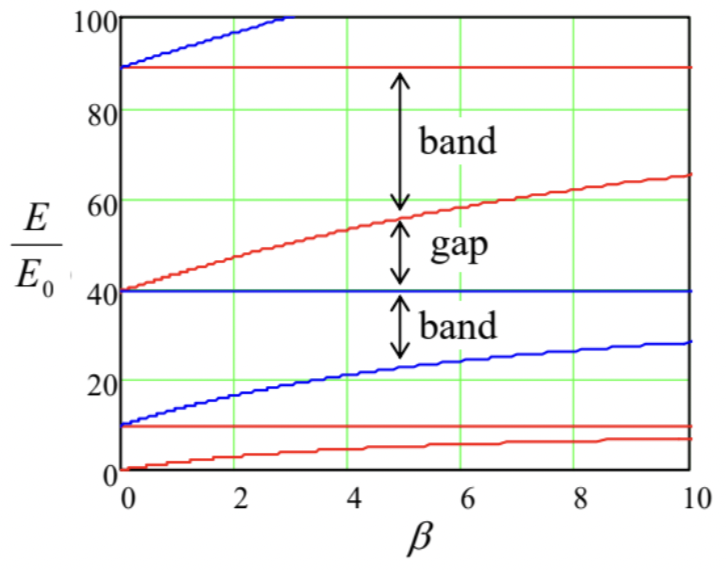Fig. 2.30. Curvas características de la ecuación de Schrödinger para el peine Dirac infinito (Fig. 24).

Estas gráficas (en matemáticas, comúnmente llamadas curvas características, mientras que en la física aplicada, diagramas de borde de banda) muestran, en primer lugar, que en pequeño\(\beta\), todos los anchos de brecha de energía son iguales y proporcionales a este parámetro, y por lo tanto a\(w\). Esta característica está en plena concordancia con la conclusión principal (224) de nuestro análisis general del límite de potencial débil, ya que para el potencial peine Dirac (Fig. 24),\[U(x)=w \sum_{j=-\infty}^{+\infty} \delta(x-j a+\text { const })\] todas las amplitudes armónicas de Fourier, definidas por la Ec. (207), son iguales por magnitud:\(\left|U_{l}\right|=W / a\). A medida\(\beta\) que se incrementa aún más, las brechas crecen y las bandas de energía permitidas se contraen, pero más bien lentamente. Esto también es natural, ya que, como muestra la Ec. (79), la transparencia\(\mathscr{T}\) de las barreras delta-funcionales que separan los estados cuasilocalizados (y por lo tanto los parámetros de acoplamiento\(\delta_{n} \propto \mathscr{T}^{/ 2}\) que participan en la teoría del límite general de unión estrecha) disminuye con \(w \propto \beta\)muy poco a poco.

Estas características pueden compararse con las de funciones periódicas más realistas y relativamente simples\(U(x)\), por ejemplo el potencial sinusoidal\(U(x)=A \cos (2 \pi x / a)-\) ver Fig. 31a. Para este potencial, la ecuación estacionaria de Schrödinger (53) toma la siguiente forma:\[-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+A \cos \frac{2 \pi x}{a} \psi=E \psi .\] Mediante la introducción de variables adimensionales\({ }^{66}\)\[\xi \equiv \frac{\pi x}{a}, \quad \alpha \equiv \frac{E}{E^{(1)}}, \quad 2 \beta \equiv \frac{A}{E^{(1)}},\] donde\(E^{(1)}\) se define por la Ec. (221) con\(n=1\), la Ec. (227) se reduce a la forma canónica del bien estudiada ecuación de Mathieu\(^{67}\)

Fig. 2.31. Otros dos perfiles simples de potencial periódico: (a) el potencial sinusoidal (“Mathieu”) y (b) el potencial de Kronig-Penney.

Fig. 2.31. Otros dos perfiles simples de potencial periódico: (a) el potencial sinusoidal (“Mathieu”) y (b) el potencial de Kronig-Penney.

La Figura 32 muestra las curvas características de esta ecuación. Vemos que ahora en pequeño\(\beta\) la primera brecha energética crece mucho más rápido que las más altas:\(\Delta_{n} \propto \beta^{n}\). Esta característica está de acuerdo con el resultado de acoplamiento débil\(\Delta_{1}=2\left|U_{1}\right|\), que es válido sólo en la aproximación lineal en\(U_{n}\), porque para el potencial Mathieu,\(U_{l}=A\left(\delta_{l,+1}+\delta_{l,-1}\right) / 2\). Otra característica claramente visible es la contracción exponencialmente rápida de las bandas de energía permitidas en\(2 \beta>\alpha\) (en la Fig. 32, a la derecha desde la línea discontinua), es decir, at\(E<A\). Puede explicarse fácilmente por nuestro resultado de aproximación de unión estrecha\((206)\): tan pronto como la energía propia cae significativamente por debajo del máximo potencial\(U_{\max }=A\) (ver Fig. 31a), los estados cuánticos en los pozos potenciales adyacentes se conectan solo mediante túneles a través de barreras potenciales relativamente altas que separan estos pozos, de manera que las amplitudes de acoplamiento\(\delta_{n}\) se vuelven exponencialmente pequeñas - véase, por ejemplo, la Ec. (189).

Fig. 2.32. Curvas características de la ecuación de Mathieu. La línea discontinua corresponde a la igualdad\(\alpha=2 \beta\), es decir\(E\)\(=A \equiv U_{\max }\), que separa las regiones de tunelización bajo barrera y movimiento sobre barrera. Adaptado de la Fig. 28.2.1 en http://dlmf.nist.gov. (Contribución del Gobierno de Estados Unidos, no sujeta a derechos de autor).

Otro perfil periódico simple es el potencial de Kronig-Penney, mostrado en la Fig. 31b, que da expresiones analíticas relativamente simples para las curvas características. Su ventaja es una ley más realista de la disminución de los armónicos de Fourier\(U_{l}\) en\(l \gg>1\), y por lo tanto de las brechas de energía en el límite de potencial débil:

\[\Delta_{n} \approx 2\left|U_{n}\right| \propto \frac{U_{0}}{n}, \text { at } E \sim E^{(n)} \gg U_{0} .\]Dejando un análisis detallado del potencial de Kronig-Penney para el ejercicio del lector, permítanme concluir esta sección abordando el efecto de la modulación potencial sobre el número de autoestados en sistemas 1D de una longitud grande pero finita\(l \gg a, k^{-1}\). Sorprendentemente, el teorema de Bloch hace elemental el análisis de este problema, por arbitrario\(U(x)\). En efecto, supongamos que\(l\) se compone de un número entero de periodos\(a\), y sus extremos son descritos por condiciones de límite similares - ambos supuestos evidentemente intrascendentes para\(l \gg>a\). Entonces, según la Ec. (210), las condiciones límite imponen, sobre el cuasimomentum\(q\), exactamente la misma condición de cuantificación que tuvimos\(k\) para un movimiento 1D libre. De ahí que en lugar de la Ec. (1.100), podamos escribir\[d N=\frac{l}{2 \pi} d q,\] con el cambio correspondiente de la regla de suma:\[\sum_{q} f(q) \rightarrow \frac{l}{2 \pi} \int f(q) d k .\] Como resultado, la densidad de estados en el\(1 \mathrm{D}\) espacio q\(d N / d q=l / 2 \pi\),, ¡no depende en absoluto del perfil potencial! Obsérvese, sin embargo, que el perfil sí afecta la densidad de estados en la escala energética,\(d N / d E\). Como ejemplo extremo, en la parte inferior y en la parte superior de cada banda de energía tenemos\(d E / d q\)\(\rightarrow 0\), y por lo tanto\[\frac{d N}{d E}=\frac{d N}{d q} / \frac{d E}{d q}=\frac{l}{2 \pi} / \frac{d E}{d q} \rightarrow \infty\] este efecto de concentración de estado en los bordes de banda/brecha (que sobrevive también en dimensionalidades espaciales más altas) tiene implicaciones importantes para la operación de varios dispositivos electrónicos y ópticos importantes, en particular láseres semiconductores y diodos emisores de luz.

---

\({ }^{47}\)Esta fórmula será más fácil de probar después de que hayamos discutido las propiedades de las matrices Pauli en el Capítulo\(4 .\)

\({ }^{48}\)En la física y electrónica de estado sólido (especialmente semiconductores), el término bandgaps es más común.

\({ }^{49}\)Este es un modelo 1D razonable, por ejemplo, para cristales en estado sólido, cuyas muestras pueden presentar hasta átomos o moléculas\(\sim 10^{9}\) similares en cada dirección de la red cristalina.

\({ }^{50}\)Una imagen clásica razonablemente justa\(\Delta \varphi\) es el ángulo geométrico entre objetos similares, por ejemplo, clips similares, unidos a distancias iguales a una banda elástica larga y uniforme. Si los extremos de la banda están retorcidos, el giro se distribuye equitativamente entre los períodos de la estructura, lo que representa la constancia de\(\Delta \varphi\). (Tengo que confesar que, por la falta de tiempo, esta fue la única “demostración de conferencias” en mis cursos de QM de Stony Brook).

\({ }^{51}\)Nombrado así por F. Bloch quien aplicó este concepto a la mecánica de las olas en 1929, es decir, muy poco después de su formulación. Tenga en cuenta, sin embargo, que una afirmación equivalente en matemáticas, llamada teorema de Floquet, se conoce desde al menos 1883.

\({ }^{52}\)Voy a recuperar este rigor en dos pasos. Más adelante en esta sección, veremos que la función obedeciendo a la ecuación (193) es efectivamente\(a\) solución a la ecuación de Schrödinger. No obstante, para ahorrar tiempo/espacio, será mejor para nosotros posponer hasta el Capítulo 4 la prueba de que cualquier función propia de la ecuación, con condiciones de límite periódicas, obedece al teorema de Bloch. Como recompensa parcial por este retraso, esa prueba será válida para una dimensionalidad espacial arbitraria.

\({ }^{53}\)El producto\(\hbar q\), que tiene la dimensionalidad del momento lineal, se llama cuasimomentum o (especialmente en la física de estado sólido) el “momentum cristalino” de la partícula. Informalmente, es muy conveniente (y común) usar el nombre “cuasimomentum” también para\(q\) lo desnudo, a pesar de su dimensionalidad evidentemente diferente.

\({ }^{54}\)Una razón más importante para tomar\(q\) como argumento es que para un potencial periódico general\(U(x)\), el impulso de la partícula no\(\hbar k\) está relacionado únicamente con\(E\), mientras que (según el teorema de Bloch) el cuasimomentum\(\hbar q\) es.

\({ }^{55}\)A continuación, veremos varios otros ejemplos de este comportamiento. Esta regla de alternancia también es descrita por la condición de cuantificación de Wilson-Sommerfeld (110).

\({ }^{56}\)Los beneficios de una notación tan inusual del índice de suma (\(l\)"en lugar de, digamos,\(l\)) quedarán claros en unas pocas líneas.

\({ }^{57}\)Por cierto, el sistema es muy eficiente para la solución numérica rápida de la ecuación estacionaria de Schrödinger para cualquier perfil periódico\(U(x)\), aunque para describir potenciales con grandes\(U_{n}\), este enfoque puede requerir tomar en cuenta un correspondientemente gran número de amplitudes de Fourier\(u_{l}\).

\({ }^{58}\)Además, posiblemente, un potencial constante\(U_{0}\), que como se discutió en el Capítulo 1, siempre puede tomarse para la referencia energética. En consecuencia, en los siguientes cálculos, tomaré\(U_{0}=0\) para simplificar las fórmulas.

\({ }^{59}\)Este método es tan poderoso que su versión multidimensional no es mucho más compleja que la versión 1D descrita aquí - véase, por ejemplo, la Sec. \(3.2\)en el libro de texto clásico de J. Ziman, Principles of the Theory of Solids,\(2^{\text {nd }}\) ed., Cambridge U. Press,\(1979 .\)

\({ }^{60}\)Permítanme esperar que la diferencia entre este nuevo entero y la masa de la partícula, ambas llamadas\(m\), quede absolutamente clara desde el contexto.

\({ }^{61}\)Físicamente,\(\gamma \hbar \equiv \hbar(\pi n / a) / m=\hbar k^{(n)} / m\) es solo la velocidad de una partícula clásica libre con energía\(E^{(n)}\).

\({ }^{62}\)A partir de esa cifra, también queda claro que en el límite de potencial débil, el ancho\(\Delta E_{n}\) de la banda de\(n^{\text {th }}\) energía es solo\(E^{(n)}\)\(-E^{(n-1)}-\) ver la Ec. (221). Tenga en cuenta que esta es exactamente la distancia entre los niveles de energía adyacentes del pozo potencial 1D más simple de profundidad infinita\(-\) cf. Ec. (1.85).

\({ }^{63}\)Véase, por ejemplo, CM Sec. \(6.1\)y en particular la Fig. \(6.2\).

\({ }^{64}\)En realidad, podríamos obtener fácilmente este diagrama en la sección anterior, para el sistema de dos pozos de potencial débilmente acoplados (Fig. 21), si asumimos que los pozos son ligeramente diferentes.

\({ }^{65}\)En el lenguaje de la dispersión de ondas de Broglie, que se discutirá en la Sec. 3.3, la Ec. (220) puede interpretarse como la condición de que cada una de estas ondas, dispersas en el armónico de\(n^{\text {th }}\) Fourier del perfil potencial, interfiera constructivamente con su contraparte, lo que lleva a una fuerte mejora de su interacción.

\({ }^{66}\)Obsérvese que esta definición de\(\beta\) es cuantitativamente diferente a la del peine Dirac (226), pero en ambos casos, este parámetro es proporcional a la amplitud de la modulación potencial.

\({ }^{67}\)Esta ecuación, estudiada por primera vez en la década de 1860 por É. Mathieu en el contexto de un problema bastante práctico de vibrar cabezas de tambor elípticas (!) , tiene muchas otras aplicaciones importantes en física e ingeniería, en particular, la excitación paramétrica de oscilaciones - véase, por ejemplo, CM Sec. 5.5.