6.5: Perturbaciones dependientes del tiempo

Ahora pasemos al caso cuando la perturbación\(\hat{H}^{(1)}\) en la ecuación (1) es una función del tiempo, mientras que\(\hat{H}^{(0)}\) es independiente del tiempo. El adecuado enfoque perturbador de este problema, y sus resultados, dependen críticamente de la relación entre la frecuencia característica\(\omega\) de la perturbación y la distancia entre los niveles de energía del sistema inicial:\[\hbar \omega \leftrightarrow\left|E_{n}-E_{n^{\prime}}\right| .\] En el caso de que todas las frecuencias esenciales de un perturbación son muy pequeñas en el sentido de la Ec. (74), nos encontramos ante el llamado cambio adiabático de parámetros, que pueden tratarse esencialmente como una perturbación independiente del tiempo - ver las secciones anteriores de este capítulo). La observación más interesante aquí es que la perturbación adiabática no permite ninguna transferencia significativa de la probabilidad del sistema de un estado propio a otro. Por ejemplo, en el límite WKB del movimiento orbital, la regla de cuantificación de Bohr y su modificación Wilson-Sommerfeld (2.110) garantizan que la integral\[\oint_{C} \mathbf{p} \cdot d \mathbf{r},\] tomada a lo largo de la trayectoria clásica de la partícula, es una invariante adiabática, es decir, no cambia a un cambio lento de los parámetros del sistema. (Es curioso que la mecánica clásica también garantice la invarianza de la integral (75), pero su prueba ahí\({ }^{23}\) es mucho más dura que la derivación cuántico-mecánica de este hecho, realizada en la Sec. 2.4.) Es por ello que incluso si la perturbación se agranda con el tiempo (mientras cambia lo suficientemente lento), podemos esperar que persista la clasificación de los autoestados y los valores propios.

Pasemos al caso más difícil cuando ambos lados de la Ec. (74) son comparables, utilizando para esta discusión el cuadro Schrödinger de la dinámica cuántica, dado por la Ec. (4.158). Combinándolo con la Ec. (1), obtenemos la ecuación de Schrödinger en la forma\[i \hbar \frac{\partial}{\partial t}|\alpha(t)\rangle=\left(\hat{H}^{(0)}+H^{(1)}(t)\right)|\alpha(t)\rangle .\] Muy en el espíritu de nuestro tratamiento del caso independiente del tiempo en la Sec. 1, representemos el vector ket-dependiente del tiempo del sistema con su expansión,\[|\alpha(t)\rangle=\sum_{n}|n\rangle\langle n \mid \alpha(t)\rangle,\] sobre el conjunto completo y ortonormal de lo imperturbable, vectores cet-estacionarios definidos por ecuación\[\hat{H}^{(0)}|n\rangle=E_{n}|n\rangle\] (Tenga en cuenta que estos kets\(|n\rangle\) son exactamente lo que se llamó\(\left|n^{(0)}\right\rangle\) en la Sec. 1; podemos permitirnos una notación menos voluminosa en esta sección, porque solo se discutirán los órdenes más bajos de la teoría de la perturbación.) Tapando la expansión (77), con\(n\) reemplazada por\(n\) ', en ambos lados de la ecuación (76), y luego multiplicando internamente ambos lados por el bra-vector\(\langle n|\) de otro estado no perturbado (y por lo tanto independiente del tiempo) del sistema, obtenemos el siguiente conjunto de ecuaciones diferenciales lineales y ordinarias para los coeficientes de expansión:\[i \hbar \frac{d}{d t}\langle n \mid \alpha(t)\rangle=E_{n}\langle n \mid \alpha(t)\rangle+\sum_{n^{\prime}} H_{n n^{\prime}}^{(1)}(t)\left\langle n^{\prime} \mid \alpha(t)\right\rangle,\] donde los elementos de la matriz de la perturbación, en la base de estado imperturbable, definidos de manera similar a la Ec. (8), son ahora funciones del tiempo:\[H_{n n^{\prime}}^{(1)}(t) \equiv\left\langle n\left|\hat{H}^{(1)}(t)\right| n^{\prime}\right\rangle .\] El conjunto de ecuaciones diferenciales (79), que siguen siendo exactas, puede ser útil para cálculos numéricos. \({ }^{24}\)Sin embargo, tiene un cierto inconveniente técnico, que queda claro si consideramos su solución (evidente) en ausencia de perturbación:\({ }^{25}\)

\[\langle n \mid \alpha(t)\rangle=\langle n \mid \alpha(0)\rangle \exp \left\{-i \frac{E_{n}}{\hbar} t\right\} .\]Vemos que estas soluciones oscilan muy rápido, y su modelado numérico puede representar un desafío incluso para las computadoras más rápidas. Estas oscilaciones espurias (cuya frecuencia, en particular, depende del nivel de referencia de energía) pueden ser domesticadas en parte buscando la solución general de las ecuaciones (79) en una forma inspirada en la ecuación (81):\[\langle n \mid \alpha(t)\rangle \equiv a_{n}(t) \exp \left\{-i \frac{E_{n}}{\hbar} t\right\} .\] Aquí\(a_{n}(t)\) hay nuevas funciones del tiempo (esencialmente, los estados estacionarios amplitudes de probabilidad), que pueden utilizarse, en particular, para calcular las ocupaciones de nivel dependientes del tiempo, es decir, las probabilidades\(W_{n}\) de encontrar el sistema perturbado en los niveles de energía correspondientes del sistema no perturbado:\[W_{n}(t)=|\langle n \mid \alpha(t)\rangle|^{2}=\left|a_{n}(t)\right|^{2} .\]

Enchufando la Ec. (82) a la Ec. (79), para estas funciones obtenemos fácilmente un sistema de ecuaciones ligeramente modificado:\[i \hbar \dot{a}_{n}=\sum_{n^{\prime}} a_{n^{\prime}} H_{n n^{\prime}}^{(1)}(t) e^{i \omega_{n n^{\prime}} t},\] donde los factores\(\omega_{n n}\), definidos por la relación\[\hbar \omega_{n n^{\prime}} \equiv E_{n}-E_{n^{\prime}},\] tienen el sentido físico de frecuencias de transiciones cuánticas potenciales entre las\(n^{\text {th }}\) y \(n^{, \text {th }}\)niveles de energía del sistema imperturbable. (Pronto quedarán claras las condiciones en las que efectivamente se lleven a cabo tales transiciones). Las ventajas de la Ec. (84) sobre la Ec. (79), tanto para los cálculos analíticos como numéricos, es su independencia de la referencia de energía, y frecuencias más bajas de oscilaciones de los términos del lado derecho, especialmente cuando los niveles de energía de interés están cerca uno del otro. \({ }^{26}\)

Para continuar con nuestro tratamiento analítico, centrémonos en un problema particular pero muy importante de una perturbación sinusoidal encendida en algún momento\(-\) que puede ser tomada por\(t=0\):\[\hat{H}^{(1)}(t)= \begin{cases}0, & \text { for } t<0, \\ \hat{A} e^{-i \omega t}+\hat{A}^{\dagger} e^{+i \omega t}, & \text { for } t \geq 0,\end{cases}\]

donde los operadores de amplitud de perturbación\(\ \hat{A}\) y\(\ \hat{A}^{\dagger}\), ²⁷ y por lo tanto sus elementos de matriz,

\[\ \left\langle n|\hat{A}| n^{\prime}\right\rangle \equiv A_{n n^{\prime}}, \quad\left\langle n\left|\hat{A}^{\dagger}\right| n^{\prime}\right\rangle=A_{n^{\prime} n}^{*},\]

son independientes del tiempo después del momento de encendido. En este caso, la Ec. (84) rinde

\[\ i \hbar \dot{a}_{n}=\sum_{n^{\prime}} a_{n^{\prime}}\left[A_{n n^{\prime}} e^{i\left(\omega_{n n^{\prime}}-\omega\right) t}+A_{n^{\prime} n}^{*} e^{i\left(\omega_{n n^{\prime}}+\omega\right) t}\right], \quad \text { for } t>0 .\]

Esto es, generalmente, todavía un sistema no trivial de ecuaciones diferenciales acopladas; sin embargo, permite soluciones simples y explícitas en dos límites muy importantes. Primero, supongamos que nuestro sistema inicialmente estaba definitivamente en un estado propio\(\ n^{\prime}\) (generalmente, aunque no necesariamente, en el estado base), y que las ocupaciones\(\ W_{n}\) de todos los demás niveles permanecen muy bajas todo el tiempo. (Encontraremos la condición cuando el segundo supuesto sea válido a posteriori — a partir de la solución.) Con estos supuestos,

\[\ a_{n^{\prime}}=1 ; \quad\left|a_{n}\right|<<1, \quad \text { for } n \neq n^{\prime},\]

La ecuación (88) puede integrarse fácilmente, dando

\[\ a_{n}=-\frac{A_{n n^{\prime}}}{\hbar\left(\omega_{n n^{\prime}}-\omega\right)}\left[e^{i\left(\omega_{n n^{\prime}}-\omega\right) t}-1\right]-\frac{A_{n^{\prime} n}^{*}}{\hbar\left(\omega_{n n^{\prime}}+\omega\right)}\left[e^{i\left(\omega_{n n^{\prime}}+\omega\right) t}-1\right], \quad \text { for } n \neq n^{\prime} .\]

Esta expresión describe lo que coloquialmente se llama la excitación ac de (otros) niveles de energía. Cualitativamente, muestra que la probabilidad\(\ W_{n}\) (83) de encontrar el sistema en cada estado (“en cada nivel de energía”) del sistema no tiende a ningún valor constante sino que oscila en el tiempo. También muestra que la transferencia inducida por campo ac del sistema de un estado a otro tiene un carácter claramente resonante: la ocupación máxima\(\ W_{n}\) de un número de nivel\(\ n \neq n^{\prime}\) crece infinitamente cuando la correspondiente desafinación ²⁸

\[\ \Delta_{n n^{\prime}} \equiv \omega-\omega_{n n^{\prime}},\]

tiende a cero. Esta conclusión es claramente poco realista, y es un artefacto de nuestra suposición inicial (89); de acuerdo con la Ec. (90), solo se satisface si ²⁹

\[\ \left|A_{n n^{\prime}}\right|<<\hbar\left|\omega \pm \omega_{n n^{\prime}}\right|,\]

y de ahí que no permita un análisis más profundo de la excitación resonante.

Para superar esta limitación, podemos realizar el siguiente truco, muy similar al que usamos para la transferencia al caso degenerado en la Sec. 1. Supongamos que para cierto nivel\(n\),\[\left|\Delta_{n n^{\prime}}\right|<<\omega,\left|\omega \pm \omega_{n^{\prime \prime} n}\right|,\left|\omega \pm \omega_{n^{\prime \prime} n^{\prime}}\right|, \quad \text { for all } n^{\prime \prime} \neq n, n^{\prime}\]

• la condición ilustrada en la Fig. 8. Entonces, según la ecuación (90), podemos ignorar la ocupación de todos menos dos niveles,\(n\) y\(n^{\prime}\), y también el segundo, término no resonante con frecuencia\(\omega_{n n^{\prime}}+\omega \approx 2 \omega>>\left|\Delta_{n n}\right|\) en ecuaciones (88),\({ }^{30}\) ahora escrito para dos amplitudes de probabilidad, \(a_{n}\)y\(a_{n}\).

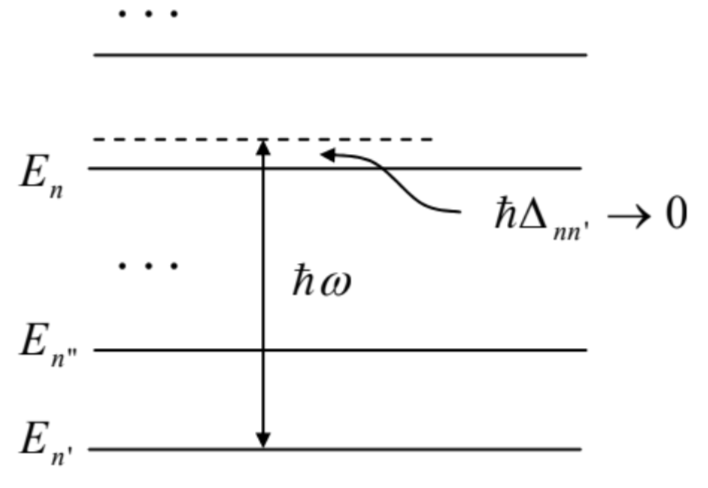Fig. 6.8. La excitación resonante de un nivel de energía.

El resultado es el siguiente sistema de dos ecuaciones lineales:\[i \hbar \dot{a}_{n}=a_{n^{\prime}} A e^{-i \Delta t}, \quad i \hbar \dot{a}_{n^{\prime}}=a_{n} A^{*} e^{i \Delta t},\] que utiliza la notación taquigráfica\(A \equiv A_{n n}\) 'y\(\Delta \equiv \Delta_{n n}\). (Voy a usar esta notación por un tiempo -hasta que otros niveles de energía se involucren, al inicio de la siguiente sección). Este sistema puede reducirse fácilmente a una forma sin dependencia explícita del tiempo de las partes de la derecha, por ejemplo, introduciendo las siguientes nuevas amplitudes de probabilidad, con los mismos módulos: de\[b_{n} \equiv a_{n} e^{i \Delta t / 2}, \quad b_{n^{\prime}} \equiv a_{n^{\prime}} e^{-i \Delta t / 2},\] modo que\[a_{n}=b_{n} e^{-i \Delta t / 2}, \quad a_{n^{\prime}}=b_{n^{\prime}} e^{i \Delta t / 2} .\] Tapando estas relaciones en la Eq. (94), obtenemos dos habituales lineales de primer orden ecuaciones diferenciales:\[i \hbar \dot{b}_{n}=-\frac{\hbar \Delta}{2} b_{n}+A b_{n^{\prime}}, \quad i \hbar \dot{b}_{n^{\prime}}=A^{*} b_{n}+\frac{\hbar \Delta}{2} b_{n^{\prime}} .\] Como ya sabe muy bien el lector, la solución general de dicho sistema es una combinación lineal de dos funciones exponenciales\(\exp \left\{\lambda_{\pm} t\right\}\), con los exponentes\(\lambda_{\pm}\) que se pueden encontrar al enchufar cualquiera de estas funciones en la Ec. (97), y requiriendo la consistencia de las dos ecuaciones algebraicas lineales resultantes. En nuestro caso, la condición de consistencia (es decir, la ecuación característica del sistema) es\[\left|\begin{array}{cc} -\hbar \Delta / 2-i \hbar \lambda & A \\ A^{*} & \hbar \Delta / 2-i \hbar \lambda \end{array}\right|=0,\] y tiene dos soluciones\(\lambda_{\pm}=\pm i \Omega\), donde\[\Omega \equiv\left(\frac{\Delta^{2}}{4}+\frac{|A|^{2}}{\hbar^{2}}\right)^{1 / 2}, \quad \text { i.e. } 2 \Omega=\left(\Delta^{2}+4 \frac{|A|^{2}}{\hbar^{2}}\right)^{1 / 2}\] Los coeficientes en los exponentes están determinados por condiciones iniciales. Si, como se suponía antes, el sistema estaba completamente en el nivel\(n^{\prime}\) inicialmente (at\(t=0\)), es decir\(a_{n^{\prime}}(0)=1, a_{n}(0)=0\), si, para que\(b_{n^{\prime}}(0)=\)\(1, b_{n}(0)=0\) también, entonces las ecuaciones (97) rinden, en particular:\[b_{n}(t)=-i \frac{A}{\hbar \Omega} \sin \Omega t,\] para que el \(n^{\text {th }}\)nivel de ocupación es\[W_{n}=\left|b_{n}\right|^{2}=\frac{|A|^{2}}{\hbar^{2} \Omega^{2}} \sin ^{2} \Omega t \equiv \frac{|A|^{2}}{|A|^{2}+(\hbar \Delta / 2)^{2}} \sin ^{2} \Omega t .\] Esta es la famosa fórmula de oscilación de Rabi\({ }^{31}\) Si la desafinación es grande en comparación con\(|A| / \hbar\), aunque todavía pequeña en el sentido de la ecuación (93), la frecuencia\(2 \Omega\) de las oscilaciones de Rabi es completamente determinado por la desafinación, y su amplitud es pequeña:\[W_{n}(t)=4 \frac{|A|^{2}}{\hbar^{2} \Delta^{2}} \sin ^{2} \frac{\Delta t}{2}<<1, \quad \text { for }|A|^{2}<<(\hbar \Delta)^{2},\]

• el resultado que podría obtenerse directamente de la Ec. (90), simplemente descuidando el segundo término en su lado derecho. Sin embargo, ahora también podemos analizar los resultados de un aumento de la amplitud de perturbación: conduce no sólo a un aumento de la amplitud de las oscilaciones de probabilidad, sino también de su frecuencia - ver Fig. 9. En última instancia, en\(|A| \gg>\hbar|\Delta|\) (por ejemplo, en la resonancia exacta,\(\Delta=0\)., es decir\(\omega_{n n}{ }^{\prime}=\omega\), para que\(\left.E_{n}=E_{n^{\prime}}+\hbar \omega\right)\), las ecuaciones (101) - (102) dan\(\Omega=|A| / \hbar\) y\(\left(W_{n}\right)_{\max }=1\), es decir, describan un periódico, completo “repumping” del sistema a partir de uno nivel a otro y atrás, con una frecuencia proporcional a la amplitud de perturbación. \({ }^{32}\)

Fig. 6.9. Las oscilaciones de Rabi para varios valores de la amplitud normalizada de perturbación ac.

Este efecto es un análogo cercano de las oscilaciones cuánticas en sistemas de dos niveles con hamiltonianos independientes del tiempo, las cuales fueron discutidas en Secs. \(2.6\)y 5.1. En efecto, volvamos a examinar, por un momento, su discusión comenzó al final de la Sec.1 de este capítulo, prestando ahora más atención a la evolución temporal del sistema bajo la perturbación. Como se argumentó en esa sección, la perturbación más general hamiltoniana levantando la doble degeneración de un nivel de energía, de manera arbitraria, tiene la matriz (28). Describamos la dinámica del sistema utilizando, nuevamente, la imagen de Schrödinger, que representa el vector ket-vector de un estado arbitrario del sistema en la forma (5.1), donde\(\uparrow\) y\(\downarrow\) son los estados independientes del tiempo de la base en que se escribe la Ec. (28) (ahora sin ninguna obligación de asociar estos estados con la\(z\) -base de cualquier giro-\(1 / 2 .\)) Entonces, la ecuación de Schrödinger (4.158) rinde\[i \hbar\left(\begin{array}{l} \dot{\alpha}_{\uparrow} \\ \dot{\alpha}_{\downarrow} \end{array}\right)=\mathrm{H}^{(1)}\left(\begin{array}{l} \alpha_{\uparrow} \\ \alpha_{\downarrow} \end{array}\right) \equiv\left(\begin{array}{ll} H_{11} & H_{12} \\ H_{21} & H_{22} \end{array}\right)\left(\begin{array}{l} \alpha_{\uparrow} \\ \alpha_{\downarrow} \end{array}\right) \equiv\left(\begin{array}{l} H_{11} \alpha_{\uparrow}+H_{12} \alpha_{\downarrow} \\ H_{21} \alpha_{\uparrow}+H_{22} \alpha_{\downarrow} \end{array}\right) .\] Como sabemos (por ejemplo, de la discusión en la Sec. 5.1), el promedio de los elementos diagonales de la matriz da solo un desplazamiento común de la energía del sistema; para el propósito del análisis dinámico, puede ser absorbida en el nivel de referencia de energía. Además, el operador hamiltoniano tiene que ser hermitiano, de manera que los elementos fuera de la diagonal de su matriz tienen que ser complejo-conjugados. Con esto, las ecuaciones (103) se reducen a la forma,\[i \hbar \dot{\alpha}_{\uparrow}=-\frac{\xi}{2} \alpha_{\uparrow}+H_{12} \alpha_{\downarrow}, \quad i \hbar \dot{\alpha}_{\downarrow}=H_{12}^{*} \alpha_{\uparrow}+\frac{\xi}{2} \alpha_{\downarrow}, \quad \text { with } \hbar \xi \equiv H_{22}-H_{11},\] que es absolutamente similar a las ecuaciones (97). En particular, estas ecuaciones describen las oscilaciones cuánticas de las probabilidades\(W_{\uparrow}=|\alpha \uparrow|^{2}\) y\(W_{\downarrow}=|\alpha \downarrow|^{2}\) con la frecuencia\(^{33}\)\[2 \Omega=\left(\xi^{2}+4 \frac{\left|H_{12}\right|^{2}}{\hbar^{2}}\right)^{1 / 2} .\] La similitud de las ecuaciones (97) y (104), y por lo tanto de las ecuaciones (99) y (105), muestra que el cuántico “habitual” las oscilaciones y las oscilaciones de Rabi tienen esencialmente la misma naturaleza física, además de que en este último caso la señal externa de CA\(\hbar \omega\) cuanta los niveles de energía separados, reduciendo efectivamente su diferencia\(\left(E_{n}-E_{n}^{\prime}\right)\) a una diferencia mucho menor \(-\Delta \equiv\left(E_{n}-E_{n}^{\prime}\right)-\hbar \omega\). Además, dado que el hamiltoniano (28) es similar a la dada por la ecuación (5.2), la dinámica de dicho sistema con dos niveles de energía acoplados, dentro de los límites (93) de la teoría de la perturbación, es completamente similar a la de un sistema de dos niveles independiente del tiempo. En particular, su estado puede ser representado de manera similar por un punto en la esfera Bloch mostrado en la Fig. 5.3, con su dinámica descrita, en la imagen de Heisenberg, por la Ec. (5.19). Este hecho es muy conveniente para la implementación experimental de sistemas de información cuántica (para ser discutido con más detalle en la Sec. 8.5), ya que permite manipulaciones de qubit en una amplia variedad de sistemas físicos con niveles de energía bien separados, utilizando ac externo (generalmente microondas u óptico) fuentes.

Obsérvese, sin embargo, que de acuerdo con la Ec. (90), si el sistema tiene niveles de energía distintos a\(n\) y\(n\) ', también quedan ocupados en cierta medida. Dado que la suma de todas las ocupaciones es igual a 1, esto significa que\(\left(W_{n}\right)_{\max }\) puede acercarse a 1 solo si la otra amplitud de excitación es muy pequeña, y por lo tanto la escala de tiempo de manipulación del estado\(\tau=2 \pi / \Omega=2 \pi \hbar /|A|\) es muy larga. El límite último en este sentido lo proporciona el oscilador armónico donde todos los niveles de energía son equidistantes, y la probabilidad de repupado entre todos ellos ocurre a tasas comparables. En particular, en este sistema la implementación de las oscilaciones completas de Rabi es imposible incluso a la resonancia exacta. \({ }^{34}\)

Sin embargo, no me gustaría que estos los detalles cuantitativos ocultaran del lector la conclusión cualitativa más importante (OK, tal vez semicuantitativa: -) del análisis de esta sección: un aumento resonante de la intensidad de transición entre niveles a\(\omega \rightarrow \omega_{n n}\). Como se mostrará más adelante en el curso, en un sistema cuántico acoplado a su entorno al menos ligeramente (de ahí en realidad, en cualquier sistema cuántico), dicho incremento va acompañado de un fuerte incremento de la absorción del campo externo, que puede medirse. Este efecto tiene numerosas aplicaciones prácticas, incluidas las espectroscopias basadas en la resonancia paramagnética electrónica (EPR) y la resonancia magnética nuclear (RMN), que se utilizan ampliamente en la ciencia de los materiales, la química y la medicina. Desafortunadamente, no voy a tener tiempo para discutir en detalle los temas y métodos técnicos relacionados (en particular, interesantes técnicas de pulsación ac, incluida la llamada interferometría de Ramsey), y tengo que referir al lector a literatura especial. \({ }^{35}\)

---

\({ }^{23}\)Véase, por ejemplo, CM Sec. 10.2.

\({ }^{24}\)Incluso si el problema analizado puede ser descrito por la ecuación de Schrödinger de mecánica ondulada (1.25), una integración numérica directa de esa ecuación diferencial parcial suele ser menos conveniente que la de las ecuaciones diferenciales ordinarias (79).

\({ }^{25}\)Esta es, por supuesto, solo una forma más general de la ecuación (1.62) de la mecánica de olas de los sistemas independientes del tiempo.

\({ }^{26}\)Obsérvese que la relación de la Ec. (84) con la ecuación inicial (79) es muy cercana a la relación del cuadro de interacción de la dinámica cuántica, discutido al final de la Sec. 4.6, con su imagen de Schrödinger, con la perturbación hamiltoniana jugando el papel de la interacción uno - comparar las ecuaciones (1 ) y la Ec. (4.206). De hecho, la ecuación (84) podría obtenerse fácilmente de la imagen de interacción, y no hice esto solo para evitar usar esta artillería pesada de bra-ket para nuestro problema actual (relativamente) simple, y por lo tanto para mantener su física más transparente.

\({ }_{27}\)La notación de los operadores de amplitud en la Ec. (86) se justifica por el hecho de que la perturbación hamiltoniana tiene que ser autounida (hermitiana), y de ahí que cada término en el lado derecho de esa relación tiene que ser un conjugado hermitiano de su contraparte, lo que evidentemente es cierto solo si los operadores de amplitud también son los conjugados hermitianos entre sí. Tenga en cuenta, sin embargo, que cada uno de estos operadores de amplitud generalmente no es hermitiano.

\({ }^{28}\)La noción de desafinación también es muy útil en la teoría clásica de las oscilaciones (véase, por ejemplo, CM Capítulo 5), donde el papel de\(\omega_{n n}\) lo juega la propia frecuencia\(\omega_{0}\) del oscilador.

\({ }^{29}\)Estrictamente hablando, una condición más es que el número de niveles de “resonancia” tampoco sea demasiado alto - ver Sec. 6.

\({ }^{30}\)El segundo supuesto, es decir, la omisión de términos no resonantes en las ecuaciones para amplitudes se llama la Aproximación de Ondas Rotativas (RWA); la misma idea en la teoría clásica de las oscilaciones es la base de lo que se suele llamar el método van der Pol, y su resultado, el reducido ecuaciones - véase, por ejemplo, CM Secs. 5.3-5.5.

\({ }^{31}\)Fue derivado en 1952 por Isaac Rabi, en el contexto de los experimentos pioneros de su grupo con la excitación ac (prácticamente, microondas) de estados cuánticos, utilizando haces moleculares en vacío.

\({ }^{32}\)Como muestran las ecuaciones (82), (96) y (99), la frecuencia más baja en el sistema es\(\omega_{1}=\omega_{n^{\prime}}-\Delta / 2+\Omega\), de manera que en\(A \rightarrow 0\),\(\hbar \omega_{1} \approx \omega_{n^{\prime}}+2|A|^{2} / \hbar \Delta\). Este desplazamiento efectivo del nivel de energía más bajo (que puede ser medido por otro campo “sonda” de una frecuencia diferente) es un caso particular del efecto ac Stark, que ya se mencionó en la Sec. 2.

\({ }^{33}\)Por cierto, la Ec. (105) da una generalización natural de las relaciones obtenidas para la frecuencia de tales oscilaciones en la Sec. 2.6, donde se asumió que los pozos de potencial acoplados eran exactamente similares, por lo que\(\xi=0\). Además, las ecuaciones (104) dan una prueba largamente prometida de las ecuaciones (2.201), y de ahí una mejor justificación de las ecuaciones (2.203).

\({ }^{34}\)A partir de la Sec. 5.5, ya sabemos lo que sucede con el estado fundamental de un oscilador en su excitación sinusoidal externa (o cualquier otra): se convierte en un estado Glauber, es decir, una superposición de todos los estados de Fock - ver Ec. (5.134).

\({ }^{35}\)Para las introducciones véase, por ejemplo, J. Wertz y J. Bolton, Electron Spin Resonance,\(2^{\text {nd }}\) ed., Wiley, 2007; J. Keeler, Understanding NMR Spectroscopy,\(2^{\text {nd }}\) ed., Wiley,\(2010 .\)