19.4: Variaciones

En las Secciones 19.1,2,3, imaginamos que el cicloide fue generado por un círculo que rodaba en sentido antihorario a lo largo de la línea$y = 2a$. También podemos imaginar variaciones como el círculo rodando en el sentido de las agujas del reloj$y = 0$, o podemos comenzar con P en la parte superior del círculo en lugar de en la parte inferior. Resumo en esta sección cuatro variaciones. La distinción entre$\psi$ y$\theta$ es la siguiente. El ángulo que hace la tangente al cicloide con el$x$ eje dirigido de manera positiva es$\psi$; es decir,$dx/dy = tan \psi$ .El círculo rueda a través de un ángulo$2 \theta$. Existe una relación simple entre$\psi$ y$\theta$, que es diferente para cada caso.

En cada figura,$x$ y$y$ se trazan en unidades de$a$. La altura vertical entre vértices y cúspides es$2a$, la distancia horizontal entre una cúspide y el siguiente vértice es$\pi a$, y la longitud del arco entre una cúspide y el siguiente vértice es$4a$.

I. Círculo rueda en sentido antihorario a lo largo$y = 2a$. P comienza en la parte inferior. Las cúspides están arriba. Un vértice está en el origen.

$$\begin{align*} x &= a(2 \theta + \sin 2 \theta ) \\[4pt] y &= 2 a \sin^2 \theta \label{19.4.2}\tag{19.4.2} \\[4pt] s &= 4a \sin \theta \label{19.4.3}\tag{19.4.3} \\[4pt] ^2 &= 8 ay \label{19.4.4}\tag{19.4.4} \\[4pt] \psi &= \theta . \label{19.4.5}\tag{19.4.5} \end{align*}$$

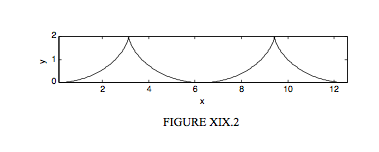
II. Círculo rueda hacia la derecha a lo largo$y = 0$. P comienza en la parte inferior. Las cúspides están abajo. Una cúspide está en el origen.

$$x = a(2\theta - sin 2\theta ) \label{19.4.6}\tag{19.4.6}$$

$$y = 2a sin^2 \theta \label{19.4.7}\tag{19.4.7}$$

$$s = 4a(1-cos \theta) \label{19.4.8}\tag{19.4.8}$$

$$s^2 = 8a(y-s) \label{19.4.9}\tag{19.4.9}$$

$$\psi = 90 \circ - \theta. \label{19.4.10}\tag{19.4.10}$$

III. Círculo rueda hacia la derecha a lo largo$y = 0$. P comienza en la parte superior. Las cúspides están abajo. Un vértice está en$x = 0$.

$$x = a( 2 \theta + \sin 2 \theta \label{19.4.11}\tag{19.4.11}$$

$$y = 2 a \cos^2 \theta \label{19.4.12}\tag{19.4.12}$$

$$s = 4 a \sin \theta \label{19.4.13}\tag{19.4.13}$$

$$s^2 = 8a(2a-y) \label{19.4.14}\tag{19.4.14}$$

$$\psi = 180 \circ - \theta . \label{19.4.15}\tag{19.4.15}$$

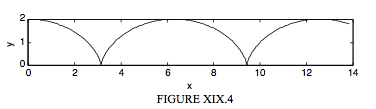
IV. Círculo rueda en sentido antihorario a lo largo$y = 2a$. P comienza en la parte superior. Las cúspides están arriba. Una cúspide está en$x = 0$.

$$x = a (2 \theta - \sin 2 \theta) \label{19.4.16}\tag{19.4.16}$$

$$y = 2a \cos^2 \theta \label{19.4.17}\tag{19.4.17}$$

$$s = 4a (1-\cos \theta) \label{19.4.18}\tag{19.4.18}$$

$$s^2 - 8as + 8a(2a - y) = 0 \label{19.4.19}\tag{19.4.19}$$

$$\psi = 90 \circ + \theta \label{19.4.20}\tag{19.4.20}$$