5.4: Extremos Libres

Elaboremos un ejemplo de oscilación forzada con un tipo diferente de condición límite. Considera las oscilaciones transversales de una cuerda con cuentas. Por definición, tomaremos cuatro cuentas para que este sea un sistema de cuatro osciladores acoplados. Sin embargo, en lugar de acoplar las cuerdas en los extremos a paredes fijas, las uniremos a anillos sin masa que son libres de deslizarse en dirección transversal sobre varillas sin fricción. Entonces se dice que la cuerda tiene sus extremos libres (al menos para movimiento transversal). Entonces el sistema se parece al diagrama de la Figura\( 5.11\), donde los osciladores se mueven hacia arriba y hacia abajo en el plano del papel: Encontremos sus modos normales.

Figura 5.11: Una cuerda con cuentas con extremos libres.

Modos normales para extremos libres

5-3
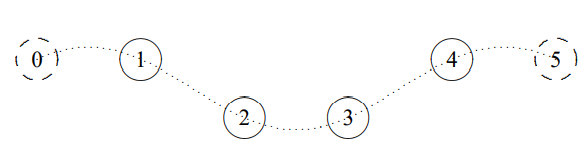
Como antes, imaginamos que esto es parte de un sistema infinito de cuentas con invarianza de traslación espacial. Esto se muestra en la Figura\( 5.12\). Aquí, los anillos sin masa que se deslizan sobre varillas sin fricción han sido reemplazados por las cuentas imaginarias (discontinuas), 0 y 5. La relación de dispersión es igual que para cualquier otra cadena infinita de cuentas, (5.39). La pregunta es, entonces, ¿qué tipo de condición límite en el sistema infinito corresponde a la condición de límite físico, que las cuentas finales estén libres por un lado? La respuesta es que debemos tener la primera cuenta imaginaria a cada lado que se mueva hacia arriba y hacia abajo con la última perla real, de modo que la cuerda de acoplamiento de la cuenta 0 sea horizontal y no ejerza ninguna fuerza de restauración transversal sobre la cuenta 1 y la cuerda de acoplamiento de la perla 5 sea horizontal y no ejerza ninguna fuerza de restauración transversal sobre Cuenta 4:\[A_{0}=A_{1} ,\]

\[A_{4}=A_{5} ;\]

Figura\( 5.12\): Satisfacer las condiciones límite en el sistema finito.

Trabajaremos en la notación en la que las cuentas están etiquetadas por sus posiciones de equilibrio. Los modos normales del sistema infinito son entonces\(e^{\pm i k x}\). Pero aún no hemos tenido que decidir dónde pondremos el origen. ¿Cómo formamos una combinación lineal de los modos exponenciales complejos\(e^{\pm i k x}\), y elegimos\(k\) ser consistentes con esta condición límite? Empecemos por (5.42). Podemos escribir la combinación lineal, sea cual sea, en la forma\[\cos (k x-\theta) .\]

Cualquier combinación lineal real de\(e^{\pm i k x}\) puede escribirse de esta manera hasta una constante multiplicativa general (ver (1.96)). Ahora si\[\cos \left(k x_{0}-\theta\right)=\cos \left(k x_{1}-\theta\right) ,\]

donde\(x_{j}\) está la posición del bloque\(j\) th, entonces

1. \(\cos (k x-\theta)\)tiene un máximo o mínimo en\(\frac{x_{0}+x_{1}}{2}\), o
2. \(k x_{1}-k x_{0}\)es un múltiplo de\(2 \pi\).

Consideremos el caso 1. Veremos que el caso 2 no da ningún modo adicional. \(\frac{x_{0}+x_{1}}{2}\)Escogeremos nuestras coordenadas para que el punto, a medio camino entre\(x_{0}\) y\(x_{1}\), sea\(x = 0\). No nos importa la normalización general, así que si la función tiene un mínimo ahí, la multiplicaremos por −1, para hacerla máxima. Así, en el caso 1, la función\(\cos (k x-\theta)\) tiene un máximo at\(x = 0\), lo que implica que podemos tomar\(\theta = 0\). Así la función es simplemente\(\cos kx\). El sistema con este etiquetado se muestra en la Figura\( 5.13\). El desplazamiento de la cuenta\(j\) th es entonces\[A_{j}=\cos [k a(j-1 / 2)] .\]

Figura\( 5.13\): El mismo sistema de osciladores etiquetados con más astucia.

Ahora debería quedar claro cómo imponer la condición límite, (5.43), en el otro extremo. Queremos tener un máximo o mínimo a medio camino entre la cuenta 4 y la cuenta 5, a\(x = 4a\). Obtenemos un máximo o mínimo cada vez que el argumento del coseno es un múltiplo integral de\(\pi\). El argumento del coseno en\(x = 4a\) es\(4ka\), donde\(k\) está el número de onda angular. Por lo tanto, la condición de límite se cumplirá si el modo tiene\(4ka = n \pi\) para entero\(n\). Entonces\[\cos [k a(4-1 / 2)]=\cos [k a(5-1 / 2)] \Rightarrow k a=\frac{n \pi}{4} .\]

Así los modos son\[A_{j}=\cos [k a(j-1 / 2)] \text { with } k=\frac{n \pi}{4 a} \text { for } n=0 \text { to } 3 .\]

Para\(n > 3\), los modos solo repiten, porque\(k \geq \pi / a\).

En (5.48),\(n = 0\) está el modo trivial en el que todas las cuentas se mueven hacia arriba y hacia abajo juntas. Esto es posible porque no hay fuerza restauradora en absoluto cuando todas las cuentas se mueven juntas. Como se discutió anteriormente (ver (5.40)) las cuentas pueden moverse todas con una velocidad constante porque\(\omega = 0\) para este modo. Tenga en cuenta que el caso 2, arriba, da el mismo modo, y nada más, porque si\(k x_{1}-k x_{0}=2 n \pi\), entonces (5.44) tiene el mismo valor para todos\(x_{j}\). Los modos restantes se muestran en\(Figures \text { } 5.14 \text{-} 5.16\). Este sistema se ilustra en el programa 5-3 en el disco del programa.

Figura\( 5.14\):\(n = 1\),\(A_{j}=\cos [(j-1 / 2) \pi / 4]\).

Figura\( 5.15\):\(n = 2\),\(A_{j}=\cos [(j-1 / 2) 2 \pi / 4]\).