6.3: Lista de verificación del capítulo

Objetivos de aprendizaje

Ahora deberías ser capaz de:

1. Tomar el límite de un sistema discreto invariante de traslación espacial a medida que la distancia entre las partes va a cero, interpretar la física del sistema continuo resultante y encontrar su relación de dispersión;
2. Utilice la serie de Fourier para configurar y resolver el problema de valor inicial para una cadena masiva con varias condiciones de límite.

Problemas

6.1. Considere la cadena continua de (6.7) - (6.10) como el límite continuo de una cadena de cuentas con\(W\) cuentas como\(W \rightarrow \infty\). Escribe el análogo de (6.8) y (6.10) para finito\(W\). Mostrar que el límite como\(W \rightarrow \infty\) rendimientos (6.10). Pista: Este es un ejercicio en la definición de una integral como límite de una suma. Pero para hacer la primera parte, necesitarás usar coordenadas normales, X o probar la identidad

\ [\ comenzar {alineado}
\ suma_ {k=1} ^ {W}\ sin\ frac {n k\ pi} {W+1}\ sin\ frac {n^ {\ prime} k\ pi} {W+1} =\ comenzar {casos} b &\ texto {si} n=n^ {\ prime}\ neq 0\\ 0 &\ texto {si} n\ neq n^ {prime}\ text {y} n, n^ {\ prime} >0\ end {cases}
\ end {alineado}\]

para una constante\(b\) y encontrar\(b\).

6.2. Hacer las integrales en (6.20). Consejo: Utilice la integración por partes y observe las cancelaciones milagrosas.

6.3. Encuentra los modos normales de la cuerda con dos extremos libres, mostrados en la Figura\( 6.7\).

6.4. Diversión con las series y fractales de Fourier

En este problema explorarás la serie de Fourier para un interesante conjunto de funciones. Considere una función de la siguiente forma, definida en el intervalo [0,1]:\[f(t)=\sum_{j=0}^{\infty} h^{j} g\left(\operatorname{frac}\left(2^{j} t\right)\right) .\]

Figura\( 6.7\): Una cuerda continua con ambos extremos libres para oscilar en la dirección transversal.

donde\ [g (t) =\ left\ {\ begin {array} {c}
1\ text {for} 0\ leq t\ leq w\\
0\ text {for} w<t<1-w\\
1\ text {for} 1-w\ leq t\ leq t\ leq 1
\ end {array}\ right.\]

y\(\operatorname{frac}(x)\) denota la parte fraccional, i.e\(\operatorname{frac}(4.39)=0.39\). \(f(t)\)así depende de los dos parámetros\(h\) y\(w\), dónde\(0 < h < 1\) y\(0 < w < 1 / 2\). Por ejemplo, para\(h = 1 / 2\) y\(w = 1 / 4\), el\(h^{0}\) término se muestra en la Figura\ (6.8.

Figura\( 6.8\): El\(h^{0}\) término en\(f(t)\) para\(h = 1 / 2\) y\(w = 1 / 4\).

Si agregamos en el\(h^{1}\) término obtenemos la imagen en Figura\( 6.9\).

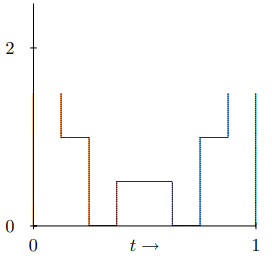
Figura\( 6.9\): Los dos primeros términos en\(f(t)\) para\(h = 1 / 2\) y\(w = 1 / 4\).

Agregar el\(h^{2}\) término da la imagen en Figura\( 6.10\), y así sucesivamente.

El resultado final es una función muy accidentada, llamada “fractal”. No se puede calcular esta función exactamente, pero puede incluir términos suficientes para llegar a cualquier precisión deseada. Porque

Figura\( 6.10\): Los tres primeros términos en\((f(t)\) para\(h = 1 / 2\) y\(w = 1 / 4\).

la función es simétrica sobre\(t = 1 / 2\), realmente solo es necesario trazarla de\(0\) a\(1 / 2\). También por la simetría, se puede expresar en términos de una serie de cosenos de Fourier,\[f(t)=\sum_{k=0}^{\infty} b_{k} \cos 2 \pi k t .\]

Mostrar que los coeficientes de Fourier están dados por\[b_{k}=\frac{2}{\pi k} \sum_{j=0}^{\xi(k)}(2 h)^{j} \sin \left(2 \pi k w / 2^{j}\right)\]

para\(k \neq 0\), y\[b_{0}=\frac{2 w}{1-h}\]

donde la función,\(\xi(k)\) es el número de veces 2 aparece como factor de\(k\). Así\(\xi(0)=\xi(1)=\xi(3)=0, \xi(2)=1, \xi(4)=2,\) etc.

Escribir un programa para mostrar e imprimir el fractal para algún conjunto de parámetros,\(h\) y\(w\). Además, mostrar la serie truncada de Fourier,\[f_{m}(t)=\sum_{k=0}^{m-1} b_{k} \cos 2 \pi k t\]

con m términos, para\(m = 5\)\(10\), y\(20\) (o más si tienes una computadora rápida).