9.3: Matrices de Transferencia

Masas en una cuerda

A continuación considere la reflexión y transmisión de dos masas sobre una cuerda, como en la Figura\( 9.5\). Ahora la invarianza de la traducción y la condición límite en\(x = \infty\) implican que\[\psi(x, t)=A e^{i k x} e^{-i \omega t}+R A e^{-i k x} e^{-i \omega t} \text { for } x \leq 0 ,\]

Figura\( 9.5\): Dos masas en una cuerda.

\[\psi(x, t)=T_{I} A e^{i k x} e^{-i \omega t}+R_{I} A e^{-i k x} e^{-i \omega t} \text { for } 0 \leq x \leq L ,\]

\[\psi(x, t)=\tau A e^{i k x} e^{-i \omega t} \text { for } x \geq L .\]

Figura\( 9.6\): El problema general de dispersión de una masa en una cuerda.

Podríamos resolver este problema de la misma manera, simplemente imponiendo condiciones de límite dos veces\(x = L\), en\(x = 0\) y en, pero hay una manera sistemática de hacerlo que es muy útil. Considere primero el problema general de dispersión de una sola masa en\(x = \ell\), con ambas ondas entrantes y salientes en ambos lados, como se muestra en la Figura\( 9.6\). Esto es lo más general posible que puede suceder en la dispersión de una sola masa, y podremos usar el resultado para hacer problemas mucho más complicados sin ningún trabajo adicional. La solución general tiene la forma\[\psi(x, t)=T_{I} A e^{i k x} e^{-i \omega t}+R_{I} A e^{-i k x} e^{-i \omega t} \text { for } x \leq \ell ,\]

\[\psi(x, t)=T_{I I} A e^{i k x} e^{-i \omega t}+R_{I I} A e^{-i k x} e^{-i \omega t} \text { for } x \geq \ell .\]

Las condiciones de contorno son continuidad,\[T_{I} e^{i k \ell}+R_{I} e^{-i k \ell}=T_{I I} e^{i k \ell}+R_{I I} e^{-i k \ell}\]

y\(F = ma\) —\ [\ begin {reunió}
T\ left (\ left. \ frac {\ parcial} {\ parcial x}\ psi (x, t)\ derecha|_ {x=\ ell^ {+}} -\ izquierda. \ frac {\ parcial} {\ parcial x}\ psi (x, t)\ derecha|_ {x=\ ell^ {-}}\ derecha)\\
= m\ frac {\ parcial^ {2}} {\ parcial t^ {2}}\ psi (\ ell, t)
\ final {reunido}\]

o\ [\ comenzar {alineado}
&i k T\ izquierda (\ izquierda (T_ {I I} -T_ {I}\ derecha) e^ {i k\ ell} +\ izquierda (R_ {I} -R_ {I}\ derecha) e^ {-i k\ ell}\ derecha)\\
&=-m\ omega^ {2}\ izquierda (T_ {yo e} ^ {i k\ ell} +R_ {I I} e^ {-i k\ ell}\ derecho).
\ end {alineado}\]

Resolviendo para\(T_{I}\) y\(R_{I}\) da\ [\ begin {aligned}
&T_ {I} =\ frac {1} {2}\ left [(2-i\ epsilon) T_ {I} -i\ épsilon R_ {I} e^ {-2 i k\ ell}\ derecha],\\
&R_ {I} =\ frac {1} {2}\ left [(2+epi\ silon) R_ {I I} +i\ epsilon T_ {I I} e^ {2 i k\ ell}\ derecho].
\ end {alineado}\]

El punto importante es que debido a la linealidad, el resultado (9.69) se puede escribir en forma de matriz:\ [\ left (\ begin {array} {l}
T_ {I}\\
R_ {I}
\ end {array}\ right) =d (\ ell)\ left (\ begin {array} {l}
T_ {I}\\
R_ {I}
\ end {array}\ derecha )\]

donde la matriz\(d(\ell)\)\ [d (\ ell) =\ frac {1} {2}\ left (\ begin {array} {cc}
(2-i\ epsilon) & -i\ epsilon e^ {-2 i k\ ell}\\
i\ epsilon e^ {2 i k\ ell} & (2+i\ épsilon)
\ end {array}\ derecha).\]

La matriz,\(d(\ell)\), es una “matriz de transferencia”. Nos permite pasar de las amplitudes en una región a las de la siguiente simplemente haciendo una multiplicación matricial. Podemos usar esto para resolver el problema de dos masas sin ningún cálculo adicional excepto una multiplicación matricial. Comparando el resultado general, (9.70), con el problema de dos masas\( 9.5\), Figura, vemos inmediatamente que\ [\ left (\ begin {array} {l}
1\\
R
\ end {array}\ right) =d (0)\ left (\ begin {array} {l}
T_ {I}\\
R_ {I}
\ end {array}\ right),\]

y\ [\ left (\ begin {array} {c}
T_ {I}\\
R_ {I}
\ end {array}\ right) =d (L)\ left (\ begin {array} {l}
\ tau\\
0
\ end {array}\ right).\]

Así\ [\ left (\ begin {array} {l}
1\\
R
\ end {array}\ right) =d (0) d (L)\ left (\ begin {array} {l}
\ tau\
0
\ end {array}\ right).\]

Haciendo la multiplicación matricial,\ [\ begin {reunió}
d (0) d (L) =\ frac {1} {4}\\
\ left (\ begin {array} {cc}
(2-i\ épsilon) ^ {2} +\ épsilon^ {2} e^ {2 i k L} & -i\ épsilon\ left ((2-i\ épsilon) e^ {-2 i k L} + (2+i\ épsilon)\ derecha)\\
i\ épsilon\ izquierda ((2-i\ épsilon) + (2 +i\ épsilon) e^ {2 i k L}\ derecha) & (2+i\ épsilon) ^ {2} +\ épsilon^ {2} e^ {-2 i k L}
\ end {array}\ right).
\ end {reunido}\]

Así\ [\ begin {reunió}
\ tau=\ frac {4} {(2-i\ épsilon) ^ {2} +\ épsilon^ {2} e^ {2 i k L}},\\
r=I\ épsilon\ izquierda ((2-i\ épsilon) + (2+i\ épsilon) e^ {2 i k L}\ derecha)\ frac\ tau} {4}.
\ end {reunido}\]

Obsérvese que la reflexión y transmisión muestra interesante estructura de resonancia. Por ejemplo, la reflexión se desvanece por\[e^{2 i k L}=-\frac{2-i \epsilon}{2+i \epsilon} .\]

En la Figura\( 9.7\),\(|\tau|\) y\(|R|\) se trazan versus\(\epsilon\) para\(k L=0.5\).

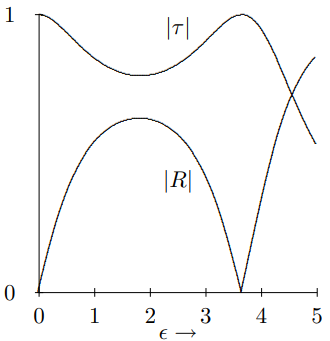
Figura\( 9.7\):\(|\tau|\) y\(|R|\) trazado versus\(\epsilon\) para dos masas en una cuerda.

\(k\)Cambios Región

Figura\( 9.8\): El problema general de dispersión para un cambio de\(k\).

Volvamos al ejemplo sencillo al inicio del capítulo de un límite entre dos regiones de cadena con diferentes valores de\(k\). Este es un ejemplo muy importante porque sus rasgos generales son característicos de muchos sistemas físicos importantes. Por ejemplo, cuando una onda de luz se encuentra con un medio transparente, el\(k\) valor cambia. Esa situación es algo más complicada por la naturaleza tridimensional de las ondas de luz y por la polarización. Sin embargo, la analogía entre (9.59) y (9.9) y (9.10) significa que podemos asumir la discusión de la cuerda directamente a ondas electromagnéticas que reflejan desde un límite dieléctrico perpendicular a la dirección de la onda. En esta sección, aplicamos el método general de matrices de transferencia discutido en la sección anterior a este importante ejemplo. Así consideramos la situación que se muestra en la Figura\( 9.8\). donde las olas tienen la forma\[\psi(x, t)=A e^{-i \omega t}\left(T_{I} e^{i k_{1} x}+R_{I} e^{-i k_{1} x}\right) \text { in } I ,\]

\[\psi(x, t)=A e^{-i \omega t}\left(T_{I I} e^{i k_{2} x}+R_{I I} e^{-i k_{2} x}\right) \text { in } I I .\]

Entonces como en (9.9) y (9.10), las condiciones límite son que\(\psi\) es continua en\(x = \ell\), lo que implica\[T_{I} e^{i k_{1} \ell}+R_{I} e^{-i k_{1} \ell}=T_{I I} e^{i k_{2} \ell}+R_{I I} e^{-i k_{2} \ell} ,\]

y que la pendiente,\(\partial \psi / \partial x\) es continua en\(x = \ell\), lo que implica\[i k_{1}\left(T_{I} e^{i k_{1} \ell}-R_{I} e^{-i k_{1} \ell}\right)=i k_{2}\left(T_{I I} e^{i k_{2} \ell}-R_{I I} e^{-i k_{2} \ell}\right) .\]

Resolviendo las ecuaciones lineales simultáneas, (9.80) y (9.81), para\(T_{I}\)\(R_{I}\) y y expresando el resultado en forma de matriz, encontramos\ [\ left (\ begin {array} {c}
T_ {I}\\
R_ {I}
\ end {array}\ right) =d\ left (k_ {1}, k_ {2},\ ell\ right)\ left (\ begin {array} {c}
T_ {I I}\\
R_ {I I}
\ end {array}\ derecho),\]

donde\ [d\ left (k_ {1}, k_ {2},\ ell\ right) =\ frac {1} {2}\ left (\ begin {array} {ll}
\ left (1+\ frac {k_ {2}} {k_ {1}}\ right) & e^ {i k_ {2}\ ell-i k_ {1}\ ell} &\ left (1-\ frac {k_ {2}} {k_ {1}}\ derecha) e^ {-i k_ {2}\ ell-i k_ {1}\ ell}\
\ izquierda (1-\ frac {k_ {2}} {k_ {1}}\ derecha) & e^ {i k_ {2}\ ell+i k_ { 1}\ ell} &\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha) e^ {-i k_ {2}\ ell+i k_ {1}\ ell}
\ end {array}\ derecha).\]

(9.82) es un resultado muy general porque\(k_{1}\),\(k_{2}\) y\(\ell\) puede ser cualquier cosa. Note que la relación es simétrica:\ [\ left (\ begin {array} {c}
\ bar {T} _ {I I}\\
R_ {I I}
\ end {array}\ right) =d\ left (k_ {2}, k_ {1},\ ell\ right)\ left (\ begin {array} {c}
T_ {I}\
R_ {I}
\ end array}\ derecho).\]

En lenguaje matricial, eso implica que\[d\left(k_{2}, k_{1}, \ell\right) d\left(k_{1}, k_{2}, \ell\right)=I .\]

También es útil usar las propiedades de multiplicación matricial para reescribir (9.83) en la siguiente forma:\[d\left(k_{1}, k_{2}, \ell\right)=b\left(k_{1}, \ell\right)^{-1} \tau\left(k_{1}, k_{2}\right) b\left(k_{2}, \ell\right) ,\]

donde\ [b (k,\ ell) =\ left (\ begin {array} {cc}
e^ {i k\ ell} & 0\\
0 & e^ {-i k\ ell}
\ end {array}\ derecha),\]

y\ [\ tau\ izquierda (k_ {1}, k_ {2}\ derecha) =d\ izquierda (k_ {1}, k_ {2}, 0\ derecha) =\ frac {1} {2}\ izquierda (\ begin {array} {ll}
\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha) &\ izquierda (1-\ frac {k_ {2}} {k_ {1}}\ derecha)\
\ izquierda (1-\ frac {k_ {2}} {k_ {1}}\ derecha) &\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha)
\ end {array}\ derecha).\]

Verá la utilidad de esto en el problema informático, (9.6).

Reflejo de una película delgada

Figura\( 9.9\): Reflejo a partir de una película delgada.

Considera la situación que se muestra en la Figura\( 9.9\). donde los números de onda son\(k_{1}\) para\(x \leq 0\),\(k_{2}\) para\(0 \leq x \leq L\) y\(k_{3}\) para\(x \geq L\). Como de costumbre, la invarianza de traducción más la condición límite en el infinito (que la onda entrante\(I\) tiene amplitud\(A\),, y que solo hay una onda saliente adentro\(III\)) implica\ [\ begin {reunió}
\ psi (x, t) =A e^ {-i\ omega t}\ left (e^ {i k_ {1} x} +R e^ {-i k_ {1} x}\ right)\ quad\ text {para} x\ leq 0\\
\ psi (x, t) =A e^ {-i\ omega t}\ left (T_ {I I} e^ {i k_ {2} x} +R_ {I I} e^ {-i k_ {2} x}\ derecha)\ text {for} 0\ leq x\ leq L,\
\ psi (x, t) =\ tau A e^ {-i\ omega t} e^ {i k_ {3} x}\ texto {para} L\ leq x.
\ end {reunido}\]

Entonces sabemos por los resultados de la sección anterior que\ [\ left (\ begin {array} {l}
1\\
R
\ end {array}\ right) =d\ left (k_ {1}, k_ {2}, 0\ right)\ left (\ begin {array} {l}
T_ {I}\\
R_ {I}
\ end {array}\ right)\]

y\ [\ left (\ begin {array} {c}
T_ {I I}\\
R_ {I I}
\ end {array}\ right) =d\ left (k_ {2}, k_ {3}, L\ derecha)\ left (\ begin {array} {l}
\ tau\\
0
\ end {array}\ right)\]

y por lo tanto\ [\ begin {reunió}
\ left (\ begin {array} {c}
1\
\
R\ end {array}\ right) =d\ left (k_ {1}, k_ {2}, 0\ right) d\ left (k_ {2}, k_ {3}, L\ right)\ left (\ begin {array} {c}
\ tau\
0
\ end {array}\ derecha). \\
d\ izquierda (k_ {1}, k_ {2}, 0\ derecha) d\ izquierda (k_ {2}, k_ {3}, L\ derecha)\\
=b\ izquierda (k_ {1}, 0\ derecha) ^ {-1}\ tau\ izquierda (k_ {1}, k_ {2}\ derecha) b\ izquierda (k_ {2}, 0\ derecha) b\ izquierda (k_ {2}, L\ derecha) ^ {-1}\ tau\ izquierda (k_ {2}, k_ {3}\ derecha) b\ izquierda (k_ {3}, L\ derecha)
\ final {reunidos}\]

A menudo nos interesa la situación\(k_{3} = k_{1}\), que describe una película (en una dimensión, una película es solo una región en\(x\)) en un medio por lo demás homogéneo. Este es entonces un análogo unidimensional del reflejo de la luz de una burbuja de jabón. Entonces la matriz de transferencia parece\ [\ begin {reunió}
\ frac {1} {4}\ left (\ begin {array} {ll}\ left (1+
\ frac {k_ {2}} {k_ {1}}\ right) &\ left (1-\ frac {k_ {2}} {k_ {1}}\ right)\\ left (1-\ frac {k_ {2}} {k_ {1}
\ right)\\ left (1-\ frac {k_ {2}} {k_ {2}} {k_ {1}}\ derecha) &\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha)
\ end { array}\ derecha)\ left (\ begin {array} {cc}
e^ {-i k_ {2} L} & 0\\
0 & e^ {i k_ {2} L}
\ end {array}\ right)\
\ left (\ begin {array} {ll}
\ left (1+\ frac {k_ {1}} {k_ {2}}\ right) &\ left (1-\ frac {k_ {1}} {k_ {2}}\ derecha)\\
\ izquierda (1-\ frac {k_ {1}} {k_ {2}}\ derecha) &\ izquierda (1+\ frac {k_ {1}} {k_ {2}}\ derecha)
\ end {array}\ derecha)\ izquierda (\ begin {array} {cc}
e^ {i k_ {1} L} & 0\\
0 & e^ {-i k_ {1} L}
\ end array}\ derecha)
\ end {reunido}\]

Por lo tanto\[1=\left(\cos k_{2} L-i \frac{k_{1}^{2}+k_{2}^{2}}{2 k_{1} k_{2}} \sin k_{2} L\right) e^{i k_{1} L} \tau\]

y\[R=-\left(i \frac{k_{1}^{2}-k_{2}^{2}}{2 k_{1} k_{2}} \sin k_{2} L\right) e^{i k_{1} L} \tau\]

o\[\tau=\left(\cos k_{2} L-i \frac{k_{1}^{2}+k_{2}^{2}}{2 k_{1} k_{2}} \sin k_{2} L\right)^{-1} e^{-i k_{1} L}\]

y\[R=-\left(i \frac{k_{1}^{2}-k_{2}^{2}}{2 k_{1} k_{2}} \sin k_{2} L\right)\left(\cos k_{2} L-i \frac{k_{1}^{2}+k_{2}^{2}}{2 k_{1} k_{2}} \sin k_{2} L\right)^{-1} .\]

Aquí vemos el fenómeno de la transmisión resonante. La onda no se refleja en absoluto si el grosor de la película es un número integral o semiintegral de longitudes de onda. Obsérvese, también\(k_{2} \rightarrow k_{1}\), que cuando,\(\tau \rightarrow 1\) y\(R \rightarrow 0\) como deberían, porque en este límite no hay límite.

La reflexión en (9.98) varía rápidamente con\(k_{2}\), como se muestra en la Figura\( 9.10\), donde se grafica la intensidad de la onda reflejada versus\(k_{2}\) para relación fija\(k_{1} / k_{2} = 3\). Es esta rápida variación de la intensidad de la luz reflejada en función de la longitud de onda la que es responsable de los patrones de color familiares en películas delgadas como pompas de jabón y manchas de aceite.

Figura\( 9.10\): Gráfica de\(|R|^{2}\) versus\(k_{2}\) para\(k_{1} / k_{2} = 3\).

Recubrimiento No Reflectante

No vamos a resolver el caso general de\(k_{1} \neq k_{3}\), simplemente porque el álgebra es un desastre. No obstante, cabe destacar un caso especial importante. Supongamos que tienes un límite entre medios en el que el número de onda de tu onda viajera son\(k_{1}\) y\(k_{3}\). Normalmente, encuentras reflexión en el límite. La pregunta es, ¿se puede agregar una capa de película intermedia con número de onda\(k_{2}\), que elimine toda reflexión? La respuesta es sí. Primero debes ajustar el número de onda en la película para que sea la media geométrica de\(k_{1}\) y\(k_{3}\), de manera que\[\frac{k_{2}}{k_{1}}=\frac{k_{3}}{k_{2}} .\]

Entonces la matriz de transferencia se convierte en\ [\ begin {alineada}
&\ frac {1} {4}\ left (\ begin {array} {ll}
\ left (1+\ frac {k_ {2}} {k_ {1}}\ right) &\ left (1-\ frac {k_ {2}} {k_ {1}}\ right)\\ left (1-\ frac {k_ {2}} {k_ {1}\ right)\\ left (1-\ frac {2}} k_ {2}} {k_ {1}}\ derecha) &\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha)
\ end {
array}\ derecha)\ left (\ begin {array} {cc}
e^ {-i k_ {2} L} & 0\\
0 & e^ {i k_ {2} L}
\ end {array}\ right)\\
&\ left (\ begin {array} {cc}
\ left (1+\ frac {k_ {2}} {k_ {1}}\ right) &\ left (1-\ frac {k_ {2}} {k_ {1}}\ derecha)\\
\ izquierda (1- \ frac {k_ {2}} {k_ {1}}\ derecha) &\ izquierda (1+\ frac {k_ {2}} {k_ {1}}\ derecha)
\ end {array}\ derecha)\ izquierda (\ begin {array} {cc}
e^ {i k_ {3} L} & 0\\
0 & e^ {-i k_ {3} L}
\ end {array}\ derecha).
\ end {alineado}\]

Es fácil verificar que la reflexión se desvanece cuando hay un número integral medio impar de longitudes de onda en la región intermedia,\[k_{2} L=(2 n+1) \frac{\pi}{2} .\]

En términos cualitativos, la reflexión desaparece debido a una interferencia destructiva entre las ondas reflejadas de los dos límites. Esto tiene aplicaciones prácticas para recubrimientos no reflectantes para componentes ópticos.