11.2: Límites de plano

Las olas viajeras más fáciles de discutir en dos y tres dimensiones son las “ondas planas”, soluciones en el sistema infinito de la forma\[\psi(r, t)=A e^{i(\vec{k} \cdot \vec{r}-\omega t)} .\]

Esto describe una onda que viaja en la dirección del vector onde-número,\(\vec{k}\), con la velocidad de fase en el medio. El desplazamiento (o lo que sea) es constante en planos de constante\(\vec{k} \cdot \vec{r}\), que son perpendiculares a la dirección del movimiento,\(\vec{k}\). Pronto estudiaremos olas viajeras más complicadas, cuando discutamos la difracción. Después aprenderemos a describir “haces” de luz o sonido u otras ondas que son las ondas viajeras con las que solemos trabajar. Veremos cómo describirlos como superposiciones de ondas planas. Por ahora, se puede pensar en una onda plana como algo así como la onda viajera que encontraría dentro de un haz amplio y coherente, o muy lejos de una pequeña fuente de luz casi monocromática, luz con una frecuencia definida. Eso debería ser suficiente para darte una imagen física de los fenómenos que discutimos en esta sección.

Estamos más interesados en las ondas como la luz y el sonido. Sin embargo, es mucho más fácil discutir las oscilaciones transversales de una membrana bidimensional, y muchos de nuestros ejemplos estarán en ese sistema. Hay dos razones. Una es que una membrana bidimensional es más fácil de visualizar en papel bidimensional. La otra razón es que la física es muy sencilla, por lo que podemos concentrarnos en las propiedades de la onda. Intentaremos señalar dónde se complican las cosas para otro tipo de fenómenos de olas.

Considera dos membranas bidimensionales estiradas en el\(z = 0\) plano, como se muestra en la Figura\( 11.5\). Pues\(x < 0\), supongamos que la densidad de masa superficial es\(\rho_{s}\) y la tensión superficial\(T_{s}\). Pues\(x > 0\), supongamos que la densidad de masa superficial es\(\rho_{s}^{\prime}\) y la tensión superficial\(T_{s}^{\prime}\). Este es un análogo bidimensional del sistema de cuerdas que discutimos extensamente en el capítulo 9. El límite entre las dos membranas debe suministrar una fuerza (en este caso, una fuerza constante por unidad de longitud) en la\(x\) dirección para soportar la diferencia entre las tensiones, como en el sistema de la Figura\( 9.2\). No obstante, asumiremos que sea cual sea el mecanismo que suministre esta fuerza, es sin masa, sin fricción e infinitamente flexible.

Figura\( 11.5\): Línea de fase constante en una onda plana que se aproxima a un límite.

Ahora de nuevo, podemos considerar el reflejo de las olas viajeras. Así, supongamos que hay, en esta membrana, una onda plana con amplitud\(A\) y número de onda\(\vec{k}\) para\(x < 0\), viajando hacia el límite en\(x = 0\). La condición de que la onda está viajando hacia el límite se puede escribir en términos de los componentes de\(\vec{k}\) como\[k_{x}>0 .\]

Nos gustaría saber qué ondas son producidas por esta onda entrante debido a la reflexión y transmisión en el límite,\(x = 0\). Por razones generales de invarianza de traducción espacial, esperamos que la solución tenga la forma\ [\ begin {alineada}
\ psi (r, t) =A e^ {i (\ vec {k}\ cdot\ vec {r} -\ omega t)} +\ sum_ {\ alpha} R_ {\ alpha} A e^ {i\ left (\ vec {k} _ {\ alpha}\ cpunto\ vec {r} -\ omega t\ derecha)} &\ texto {para} x\ leq 0\\
\ psi (r, t) =\ suma_ {\ beta}\ tau_ {\ beta} A e^ {i\ izquierda (\ vec {k} _ _ {\ beta}\ cdot\ vec {r} -\ omega t\ derecha)} &\ texto {para} x\ geq 0
\ end {alineado}\]

\[\vec{k}_{\alpha}^{2}=\omega^{2} \frac{\rho_{s}}{T_{s}} ; \quad \vec{k}_{\beta}^{2}=\omega^{2} \frac{\rho_{s}^{\prime}}{T_{s}^{\prime}} ,\]

y\[k_{\alpha x}<0 \text { and } k_{\beta_{x}}>0 \text { for all } \alpha \text { and } \beta .\]

El\(\alpha\) y\(\beta\) en (11.30) recorre todas las ondas transmitidas y reflejadas. Mostraremos en breve que solo uno de cada uno contribuye para una condición de límite plano en\(x = 0\), pero (11.30) es completamente general, siguiendo solo de la invarianza de la traducción espacial. Tenga en cuenta que hemos puesto en condiciones de límite\(\pm \infty\) al exigir (11.29) y (11.32). A excepción de la onda entrante con amplitud\(A\), todas las otras ondas se están alejando del límite. Pero aún no hemos puesto en la condición límite en\(x = 0\).

Ley de Snell — el límite invariante de la traducción

11-2 Por
lo que sabemos por consideraciones de la física en\(\pm \infty\), las ondas reflejadas y transmitidas podrían ser una superposición complicada de un número infinito de ondas planas que van en varias direcciones alejadas del límite. De hecho, si el límite tuviera forma irregular, eso es exactamente lo que esperaríamos. Es el hecho de que el límite,\(x = 0\), es en sí mismo invariante bajo las traducciones espaciales en las\(y\) direcciones que nos permite reducir el número infinito de parámetros en (11.30) a sólo dos. Debido a que las traducciones en la\(y\) dirección dejan invariante todo el sistema, incluyendo el límite, podemos encontrar soluciones en las que todos los componentes tienen la misma\(y\) dependencia irreducible. Si la onda entrante es proporcional a\[e^{i k_{y} y} ,\]

entonces todos los componentes de (11.30) también deben ser proporcionales a\(e^{i k_{y} y}\). De lo contrario no hay manera de satisfacer la condición de límite en\(x = 0\) absoluto\(y\). Eso significa que\[k_{\alpha y}=k_{y}, \quad k_{\beta_{y}}=k_{y} .\]

Pero (11.34), junto con (11.31) y (11.32), determina completamente los vectores de onda\(\vec{k}_{\alpha}\) y\(\vec{k}_{\beta}\). Entonces (11.30) se convierte en ²\ [\ begin {alineado}
\ psi (r, t) =A e^ {i\ vec {k}\ cdot\ vec {r} -i\ omega t} +R A e^ {i\ vec {k}\ cdot\ vec {r} -i\ omega t}\ equiv\ psi_ {-} (r, t) &\ text para} x\ leq 0\\
\ psi (r, t) =\ tau A e^ {i\ vec {k} ^ {\ prime}\ cdot\ vec {r} -i\ omega t}\ equiv\ psi_ {+} (r, t) & &\ texto {para} x\ geq 0
\ end {alineado}\]

donde\[\tilde{k}_{y}=k_{y}, \quad k_{y}^{\prime}=k_{y} ,\]

y\[\tilde{k}_{x}=-\sqrt{\omega^{2} / v^{2}-k_{y}^{2}}=-k_{x}, \quad k_{x}^{\prime}=\sqrt{\omega^{2} / v^{\prime 2}-k_{y}^{2}} ,\]

con\[v=\sqrt{\frac{T_{s}}{\rho_{s}}}, \quad v^{\prime}=\sqrt{\frac{T_{s}^{\prime}}{\rho_{s}^{\prime}}} .\]

Lo entretenido de (11.35) - (11.37) es que sabemos todo sobre las direcciones de las ondas reflejadas y transmitidas, aunque ni siquiera hemos mencionado los detalles de la física en el límite. Para obtener las indicaciones, solo necesitábamos la invarianza bajo las traducciones en la\(y\) dirección. Los detalles de la física del límite entran sólo cuando queremos calcular\(R\) y\(\tau\). Las direcciones de las ondas reflejadas y transmitidas son las mismas para cualquier sistema con un límite de traslación invariante. Obviamente, este argumento funciona también en tres dimensiones. De hecho, si simplemente elegimos nuestras coordenadas para que el límite sea el\(x = 0\) plano y la onda esté viajando en el\(y\) plano\(x\) -, entonces nada depende de la\(z\) coordenada y el análisis es exactamente el mismo que el anterior. Por ejemplo, podemos aplicar estos argumentos directamente a las ondas electromagnéticas. Para las ondas electromagnéticas en un medio transparente, debido a que la velocidad de fase es\(v_{\phi}=\omega / k\), el índice de refracción\(n\),, es proporcional a\(k\),\[n=\frac{c}{v_{\varphi}}=k \frac{c}{\omega} .\]

(11.36) - (11.37) muestra que la onda reflejada sale en el mismo ángulo que la onda entrante porque la única diferencia entre los\(k\) vectores de las ondas entrante y reflejada es un cambio del signo del\(x\) componente. Así, el ángulo de incidencia es igual al ángulo de reflexión. Esta es la regla de la “reflexión especular”. De (11.36), también podemos derivar la ley de refracción de Snell para el ángulo de la onda refractada. Si\(\theta\) es el ángulo que hace la onda incidente con la perpendicular al límite, y\(\theta^{\prime}\) es el ángulo correspondiente para la onda transmitida, entonces (11.36) implica\[k \sin \theta=k^{\prime} \sin \theta^{\prime} .\]

Para las ondas electromagnéticas, podemos reescribir esto como\[n \sin \theta=n^{\prime} \sin \theta^{\prime} .\]

Por ejemplo, cuando una onda electromagnética en el aire se encuentra con una superficie plana de vidrio en ángulo\(\theta\),\(n^{\prime}>n\) en (11.41). La onda se refracta hacia la perpendicular a la superficie. Esto se ilustra en la Figura\( 11.6\) para\(n^{\prime}>n\).

Figura\( 11.6\): Reflexión y transmisión desde un límite.

Ahora terminemos la solución para el problema de la membrana resolviendo para\(R\) y\(\tau\) en (11.35). Para ello, por fin debemos discutir con más detalle las condiciones de los límites. Una es que la membrana es continua, lo que a partir de la forma, (11.35), implica\[\left.\psi_{-}(r, t)\right|_{x=0}=\left.\psi_{+}(r, t)\right|_{x=0} ,\]

o\[1+R=\tau .\]

La otra es que la fuerza vertical sobre cualquier longitud pequeña de la membrana es cero. La fuerza sobre una pequeña longitud,\(d \ell\), del límite en el punto,\((0, y, 0)\), de la membrana para\(x < 0\) viene dada por\[-\left.T_{s} d \ell \frac{\partial \psi_{-}(r, t)}{\partial x}\right|_{x=0} .\]

Esto es análogo al ejemplo unidimensional ilustrado en la Figura\( 8.6\). La fuerza de tensión superficial es perpendicular al límite, por lo que para pequeños desplazamientos, solo importa la pendiente del desplazamiento en la\(x\) dirección. La pendiente en la\(y\) dirección no aporta ninguna contribución a la fuerza vertical a primer orden en el desplazamiento. Asimismo, la fuerza sobre una pequeña longitud,\(d \ell\), del límite en el punto,\((0, y, 0)\), desde la membrana para\(x > 0\) viene dada por\[\left.T_{s}^{\prime} d \ell \frac{\partial \psi_{+}(r, t)}{\partial x}\right|_{x=0} .\]

Por lo tanto, la otra condición límite es\[\left.T_{s}^{\prime} d \ell \frac{\partial \psi_{+}(r, t)}{\partial x}\right|_{x=0}=\left.T_{s} d \ell \frac{\partial \psi_{-}(r, t)}{\partial x}\right|_{x=0} ,\]

o\[T_{s}^{\prime} k_{x}^{\prime} \tau=T_{s} k_{x}(1-R) .\]

Así la solución es\[\tau=\frac{2}{1+r}, \quad R=\frac{1-r}{1+r},\]

donde\[r=\frac{T_{s}^{\prime} k_{x}^{\prime}}{T_{s} k_{x}} .\]

Se puede ver en (11.48) y (11.49) que podemos ajustar la tensión superficial para hacer que la onda reflejada desaparezca incluso cuando haya un cambio en la longitud del\(\vec{k}\) vector de un lado del límite al otro. Es útil pensar en la refracción en este límite, porque nos permitirá visualizarla de una manera sencilla. Si\(r = 1\) en (11.48), entonces\(R = 0\) y\(\tau=1\). No hay onda reflejada y la onda transmitida tiene la misma amplitud que la onda entrante. Así, en cada región, hay una sola onda plana. Recuerde que una onda plana consiste en líneas infinitas de fase constante perpendiculares al\(\vec{k}\) vector, moviéndose en la dirección del\(k\) vector con la velocidad de fase,\(v_{\varphi}=\omega /|\vec{k}|\). En particular, supongamos que miramos líneas en las que la fase es cero, así que eso\(\psi=A\). La distancia perpendicular entre dos de tales líneas es la longitud de onda\(2 \pi /|\vec{k}|\), debido a que la diferencia de fase entre líneas vecinas es\(2 \pi\). Pero aquí está el punto. Las líneas en las dos regiones deben reunirse en el límite,\(x = 0\), para satisfacer la condición límite, (11.43). Si la amplitud de onda entrante es 1 at\(x = 0\), la amplitud de onda saliente también es 1. Las líneas donde\(\psi=A\) son continuas a través del límite,\(x = 0\). Esta situación se ilustra en la Figura\( 11.7\). Se muestran los\(\vec{k}\) vectores en las dos regiones. Observe que el ángulo de las líneas debe cambiar cuando la distancia entre ellas cambia para mantener la continuidad en el límite. En el programa 11-2, el mismo sistema se muestra en movimiento.

Figura\( 11.7\): Líneas de constante\(\psi=1\) para un sistema con refracción pero sin reflexión.

Prismas

El índice no trivial de refracción del vidrio es el bloque de construcción de muchos elementos ópticos. Hablemos del prisma. De hecho, para hacer el problema de la dispersión de las ondas de luz por prismas de manera totalmente correcta requeriría técnicas mucho más sofisticadas de las que tenemos a nuestra disposición en este momento. La razón es que el prisma no es una superficie infinita, plana con invarianza de traslación espacial. En general, tendríamos que preocuparnos por el límite. No obstante, podemos decir cosas interesantes aunque ignoremos esta complicación. La idea es pensar no en una onda plana infinita, sino en un amplio haz de luz incidente sobre una cara del prisma. Un haz ancho se comporta muy parecido a una onda plana, e ignoraremos la diferencia en este capítulo. Veremos cuáles son las diferencias en el Capítulo 13 cuando discutamos la difracción.

Figura\( 11.8\): La geometría de un prisma.

Así consideramos la siguiente situación, en la que un amplio haz de luz entra en una cara de un prisma con índice de refracción\(n\) y sale por la otra cara. La geometría se muestra en la Figura\( 11.8\) (las direcciones de las vigas están indicadas por las líneas gruesas). La cantidad interesante es\(\delta\). Esto describe cuánto ha sido desviada la dirección del haz saliente de la dirección del haz entrante por el prisma. Podemos calcularlo usando geometría simple y la ley de Snell, (11.40). De la ley de Snell\[\sin \theta_{\text {in }}=n \sin \theta_{1}\]

y\[\sin \theta_{\text {out }}=n \sin \theta_{2} .\]

Ahora para algo de geometría. \[\theta_{2}+\theta_{1}=\phi^{\prime}\]

— porque el complemento de\(\phi^{\prime}\),\(\pi-\phi^{\prime}\), junto con\(\theta^{1}\) y\(\theta^{2}\) son los ángulos de un triángulo, y así se suman a\(\pi\). \[\phi=\phi^{\prime}\]

— porque\(\phi\) y\(\phi^{\prime}\) son ángulos correspondientes de los dos triángulos rectos similares con otro ángulo agudo\(\gamma\). Así\[\delta=\xi_{1}+\xi_{2}=\theta_{\mathrm{in}}+\theta_{\mathrm{out}}-\theta_{1}-\theta_{2}=\theta_{\mathrm{in}}+\theta_{\mathrm{out}}-\phi\]

donde hemos utilizado (11.52) y (11.53). Pero para ángulos pequeños, desde (11.50) y (11.51),\[\theta_{\mathrm{in}} \approx n \theta_{1}, \quad \theta_{\mathrm{out}} \approx n \theta_{2} .\]

Así\[\delta \approx n\left(\theta_{1}+\theta_{2}\right)-\phi \approx(n-1) \phi .\]

El resultado, (11.56), es ciertamente razonable. Debe desaparecer cuando\(n \rightarrow 1\), porque no hay límite para\(n = 1\). Si las cosas son pequeñas y la respuesta es lineal, debe ser proporcional a\(\phi\).

Una de las características más familiares de un prisma resulta de la dependencia del índice de refracción,\(n\), de la frecuencia. Esto provoca que un haz de luz blanca se descomponga en colores. Para la mayoría de los materiales, el índice de refracción aumenta con la frecuencia, por lo que la luz azul es desviada más que la luz roja por el prisma. La física de la dependencia de frecuencia\(n\) es la de oscilación forzada. El índice de refracción de un material está relacionado con la constante dieléctrica (ver (9.53)), que a su vez se relaciona con la distorsión de la estructura electrónica del material causada por el campo eléctrico. Para un campo variable, esto depende de la amplitud del movimiento de las cargas ligadas dentro del material en un campo eléctrico. Debido a que estas cargas están ligadas, responden a los campos oscilantes en una onda electromagnética como una masa en un resorte sujeto a una fuerza oscilante. Sabemos por nuestros estudios de oscilación forzada que esta amplitud tiene la forma\[\sum_{\underset{\alpha}{ }^{\text {resonances }}} \frac{C_{\alpha}}{\omega_{\alpha}^{2}-\omega^{2}} ,\]

donde\(\omega_{\alpha}\) están las frecuencias resonantes del sistema y las\(C_{\alpha}\) son constantes dependiendo de los detalles de cómo actúa la fuerza sobre los grados de libertad. Podemos estimar el orden de magnitud de estas frecuencias resonantes con análisis dimensional, si recordamos que cualquier material consiste en electrones y núcleos mantenidos unidos por fuerzas eléctricas (y mecánica cuántica, por supuesto, pero no\(\hbar\) entrará en nuestra estimación excepto implícitamente, en la típica distancia atómica). Las cantidades relevantes son ³\ [\ begin {aligned}
&\ text {La carga del protón} e\ approx 1.6\ times 10^ {-19}\ mathrm {C}\\
&\ text {La masa del electrón} m_ {e}\ approx 9.11\ times 10^ {-31}\ mathrm {~kg}\\\
&\ text {Típico atómico distancia}\ quad a\ aprox 10^ {-10}\ mathrm {~m} =1\ AA\\
&\ text {La velocidad de la luz}\ quad c=299,792,458\ mathrm {~m}/\ mathrm {s}
\ end {alineado}\]

En términos de estos parámetros, adivinaríamos que la fuerza típica dentro de los materiales es de\(\frac{e^{2}}{4 \pi \epsilon 0 a^{2}}\) (de la ley de Coulomb), y así que la constante elástica es de orden\(\frac{e^{2}}{4 \pi \epsilon_{0} a^{3}}\) (la fuerza típica sobre la distancia típica). Así esperamos\[\omega_{\alpha}^{2} \approx \sqrt{\frac{e^{2}}{4 \pi \epsilon_{0} a^{3} m_{e}}}\]

y\[\lambda_{\alpha} \approx \frac{2 \pi c}{\omega_{\alpha}} \approx 2 \pi c \sqrt{\frac{4 \pi \epsilon_{0} a^{3} m_{e}}{e^{2}}} \approx 10^{-7} \mathrm{~m}=1000 \AA .\]

Esta es una longitud de onda en la región ultravioleta del espectro electromagnético, más corta que la de la luz visible. Eso significa que para la luz visible\(\omega<\omega_{\alpha}\), y por lo tanto el desplazamiento, (11.57), aumenta a medida que\(\omega\) aumenta para la luz visible. La distorsión de la estructura electrónica del material causada por un campo eléctrico variable aumenta a medida que aumenta la frecuencia en el espectro visible. Así la constante dieléctrica del material aumenta con la frecuencia. Así se desvía más la luz azul.

Por cierto, esta es la misma razón por la que el cielo es azul. La luz azul se dispersa más que la luz roja porque su frecuencia está más cerca de las resonancias importantes de las moléculas de aire.

Reflexión interna total

La situación en la que la ola viene de una región de grandes\(|\vec{k}|\) a una región de menor tamaño\(|\vec{k}|\) tiene otra característica que resulta sorprendente y muy útil. Esta situación se representa en la Figura\( 11.9\) para un sistema sin reflexión. Para pequeños,\(\theta\), como se muestra en la Figura\( 11.9\), esto se ve más bien

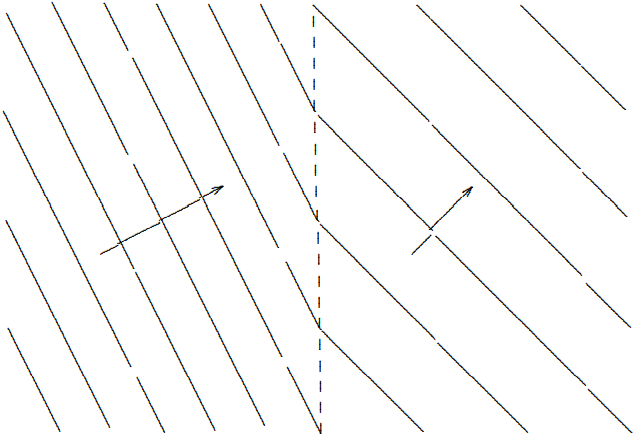
Figura\( 11.9\): Líneas de constante\(\psi=1\) para\(n^{\prime} < n\).

como Figura\( 11.7\), excepto que la onda se refracta alejándose de la perpendicular a la superficie en lugar de hacia ella. Pero supongamos que el ángulo\(\theta\) es grande, satisfactorio\[n \sin \theta / n^{\prime}>1 .\]

Entonces no hay solución de verdad\(\theta^{\prime}\) en (11.41). Por lo tanto, no puede haber onda viajera transmitida. La onda entrante debe ser totalmente reflejada por el límite. Esta es una reflexión interna total. Ocurre cuando una onda plana intenta escapar de una región de alta\(|\vec{k}|\) a una región de menor\(|\vec{k}|\) en un ángulo de pastoreo. Es ampliamente utilizado en equipos ópticos y muchas otras cosas. Investiguemos con más detalle este peculiar fenómeno.

Supongamos que partimos\(\theta = 0\) y aumentamos\(\theta\). A\(\theta\) medida que aumenta,\(k_{y}\) aumenta y\(k_{x}\) disminuye. Esto continúa hasta llegar al límite de la reflexión interna total, llamada ángulo crítico,\[\sin \theta=\sin \theta_{c} \equiv \frac{n^{\prime}}{n} .\]

Las amplitudes tanto para las ondas reflejadas como transmitidas en (11.48) también aumentan. En el ángulo crítico, se\(k_{x}\) desvanece. La amplitud para la onda reflejada es 1 y la amplitud para la onda transmitida es 2. Sin embargo, a pesar de que la onda transmitida es distinta de cero, ninguna energía se aleja del límite porque el\(\vec{k}\) vector apunta en la\(y\) dirección. A\(\theta\) medida que aumenta más allá del ángulo crítico,\(k_{y}\) continúa aumentando. Para satisfacer la relación de dispersión,\[\omega^{2}=v^{\prime 2}\left(k_{x}^{2}+k_{y}^{2}\right) ,\]

\(k_{x}\)debe ser puro imaginario! La dependencia x es entonces proporcional a\[e^{-\kappa x} \text { where } \kappa=\operatorname{Im} k_{x} .\]

Ahora la naturaleza de la condición límite en el infinito cambia. Ya no podemos exigir simplemente eso\(k_{x} > 0\). En cambio, debemos exigir\[\operatorname{Im} k_{x}>0 .\]

El signo es importante. Si\(\operatorname{Im} k_{x}\) fueran negativos, la amplitud de la onda para\(x > 0\) aumentaría con\(x\), yendo exponencialmente al infinito como\(x \rightarrow \infty\). Esto no tiene mucho sentido físico porque corresponde a una causa finita (la onda entrante para\(x < 0\)) produciendo un efecto infinito. Como veremos a continuación, también podemos llegar a esta conclusión yendo a este sistema infinito como límite de un sistema finito.

En realidad tenemos tres condiciones de límite diferentes en el infinito para esta situación:\ [\ begin {reunió}
\ operatorname {Re} k_ {x} >0\ text {for}\ theta<\ theta_ {c},\\
k_ {x} =0\ text {for}\ theta=\ theta_ {c},\\
\ operatorname {Im} k_ {x} >0\ texto {para}\ theta>\ theta_ {c}.
\ end {reunido}\]

Estos tres se pueden combinar en una condición compuesta que es válida en todas las regiones:\[\operatorname{Re} k_{x} \geq 0, \quad \operatorname{Im} k_{x} \geq 0 .\]

La condición, (11.67), es en realidad la declaración más general de la condición de límite de onda viajera saliente en el infinito. También es correcto en situaciones en las que hay amortiguación y tanto la parte real como la imaginaria de\(k_{x}\) son distintas de cero. Esta es la afirmación matemática del hecho físico de que la onda para\(x > 0\), cualquiera que sea su forma, es producida en el límite por la onda entrante.

De (11.48) y (11.49), se ve que para\(\theta>\theta_{c}\), la amplitud de la onda reflejada se vuelve compleja. No obstante, su valor absoluto sigue siendo 1. Toda la energía de la onda entrante se refleja.

Hemos visto que en las reflexiones internas totales, la onda sí penetra en la región prohibida, pero la\(x\) dependencia es en forma de una onda estacionaria exponencial, no una onda viajera. La\(y\) dependencia es la de una ola viajera. Esta es una de las muchas situaciones en las que la física obliga a la naturaleza de la solución bidimensional o tridimensional a tener diferentes propiedades en diferentes direcciones.

Es fácil ver la reflexión interna total en una pecera, un bloque de vidrio o algún otro objeto transparente rectangular con un índice de refracción significativamente mayor que 1. Se puede mirar a través de una cara del rectángulo y ver el reflejo plateado de una cara adyacente, como se ilustra en la Figura\( 11.10\).

Figura\( 11.10\): Reflejo interno total en vidrio con índice de refracción 2.

Túnel

Considere la dispersión de una onda plana en el sistema ilustrado en la Figura\( 11.11\). Esta es la misma configuración que en la Figura\( 11.10\), excepto que se ha agregado otro bloque de vidrio a una pequeña distancia,\(d\), por debajo del límite desde el cual hubo reflexión interna total. Hemos definido la\(x\) dirección positiva para estar a la baja para coherencia con la discusión de la ley de Snell, arriba. Ahora bien, ¿alguna de las luces llega al observador de abajo, o la luz todavía se refleja totalmente en el límite, como en la Figura\( 11.10\)? La respuesta es que pasa algo de luz. Como veremos en detalle en un ejemplo a continuación, la presencia del otro bloque de vidrio significa que en lugar de una condición límite en el infinito, tenemos una condición de límite a la distancia finita,\(d\).

Los detalles de este fenómeno para las ondas electromagnéticas son algo complicados por la polarización, que discutiremos en detalle en el próximo capítulo. Sin embargo, existe un proceso precisamente análogo en la oscilación transversal de membranas que podemos analizar fácilmente

Figura\( 11.11\): Un experimento sencillo para demostrar la tunelización.

De hecho, encontraremos que ya lo hemos analizado en el capítulo 9. Considere el problema de dispersión ilustrado en la Figura\( 11.12\). La región no sombreada es una membrana con menor densidad. Las flechas indican las direcciones de los\(\vec{k}\) vectores de las ondas planas. Las regiones sombreadas

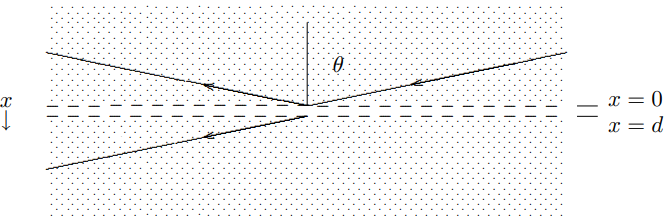
Figura\( 11.12\): Túnel en una membrana infinita.

tienen densidad de masa superficial\(\rho_{s}\) y tensión superficial\(T_{s}\). La región no sombreada, que se extiende de\(x = 0\) a\(x = d\), tiene la misma tensión superficial pero densidad de masa superficial\(\rho_{s} / 4\). Así, la relación de velocidades de fase en las dos regiones es de dos, lo mismo que la relación de aire a vidrio en la Figura\( 11.11\). Las líneas discontinuas son límites sin masa entre las diferentes membranas.

Ahora podemos preguntarnos cuáles son los coeficientes,\(R\) y\(\tau\), para la reflexión y la transmisión. Nosotros hemos hecho este problema para un solo límite anterior en este capítulo en (11.42) - (11.49). Podríamos resolver esta uniendo dos de estas soluciones utilizando las técnicas de matriz de transferencia del capítulo 9. De hecho, ni siquiera tenemos que hacer eso, porque podemos leer el resultado de (9.97) y (9.98) en la discusión de películas delgadas en el capítulo 9. El punto es que todos los términos en nuestra solución deben tener la misma\(y\) dependencia irreducible,\(e^{i k_{y} y}\), debido a la invarianza de traslación espacial de todo el sistema incluyendo el límite en la\(y\) dirección. Este factor común no juega ningún papel en las condiciones de contorno. Si lo factorizamos, lo que queda parece un problema de dispersión unidimensional. Comparando (11.47) para\(T_{s}=T_{s}^{\prime}\) (9.10), puedes ver que los análisis se vuelven iguales si hacemos los reemplazos\ [\ begin {aligned}
k_ {1} &\ rightarrow k_ {x}\\
k_ {2} &\ rightarrow k_ {x} ^ {\ prime}\\
L &\ rightarrow d
\ end {alineado}\]

donde\(k_{x}\) es el\(x\) componente del\(\vec{k}\) vector de la onda entrante en la región sombreada y\(k_{x}^{\prime}\) es el\(x\) componente del\(\vec{k}\) vector de la onda transmitida en la región no sombreada. El resultado es\[\tau=\left(\cos k_{x}^{\prime} d-i \frac{k_{x}^{2}+k_{x}^{\prime 2}}{2 k_{x} k_{x}^{\prime}} \sin k_{x}^{\prime} d\right)^{-1} e^{-i k_{x} d}\]

y\[R=\left(i \frac{k_{x}^{2}-k_{x}^{\prime 2}}{2 k_{x} k_{x}^{\prime}} \sin k_{x}^{\prime} d\right)\left(\cos k_{x}^{\prime} d-i \frac{k_{x}^{2}+k_{x}^{\prime 2}}{2 k_{x} k_{x}^{\prime}} \sin k_{x}^{\prime} d\right)^{-1} .\]

Puede ser un poco más fácil observar la intensidad de la onda transmitida, que es proporcional a\[|\tau|^{2}=\frac{2 k_{x}^{2} k_{x}^{2}}{\left(k_{x}^{4}+k_{x}^{\prime 4}\right) \sin ^{2} k_{x}^{\prime} d+2 k_{x}^{2} k_{x}^{\prime 2}} .\]

Tenga en cuenta que no hemos mencionado el ángulo crítico ni la reflexión interna total ni nada por el estilo. El motivo es que nuestro análisis en el capítulo 9 fue perfectamente general. Sigue siendo correcto incluso si el número de onda angular en la región media se vuelve imaginario. Todo lo que sucede para\(\theta\) mayor que el ángulo crítico,\(\theta_{c}\), es que\(k_{x}^{\prime}\) se vuelve imaginario. Pero esto tiene un efecto espectacular en (11.71). Si\(k_{x}^{\prime} \rightarrow i \kappa\), donde\(\kappa\) es real, entonces se deduce de la identidad de Euler, (1.57) x y (1.62), que\[\sin k_{x}^{\prime} d \rightarrow i \sinh \kappa d ,\]

donde\(\sinh\) está el “seno hiperbólico”, definido por\[\sinh x \equiv \frac{e^{x}-e^{-x}}{2} .\]

Así, para ángulos por encima del ángulo crítico, el denominador de (11.71) es una función exponencialmente creciente de\(d\) (el\(e^{\kappa d}\) término en (11.73) domina para grandes\(\kappa d\)). Por lo tanto, la intensidad de la onda transmitida disminuye exponencialmente con\(d\). En el límite de grandes\(d\), recuperamos rápidamente la reflexión interna total.

Podemos obtener una idea de lo que está sucediendo observando las condiciones de contorno en ángulos\(x = d\) por encima del ángulo crítico. Para\(x > d\), la onda tiene la forma (suprimiendo los factores comunes de\(e^{i k_{y} y}\) y\(A e^{-i \omega t}\))\[\tau e^{i k_{x} x} .\]

Porque\(0 \leq x \leq d\), la ola tiene la forma\[T_{I I} e^{-\kappa x}+R_{I I} e^{\kappa x} ,\]

donde he llamado a los coeficientes\(T_{I I}\) y\(R_{I I}\) por analogía con las ondas transmitidas y reflejadas, aunque éstas no sean ondas viajeras. Las condiciones límite en\(x = d\) son\ [\ begin {reunió}
\ tau e^ {i k_ {x} d} =T_ {I I} e^ {-\ kappa d} +R_ {I I} e^ {\ kappa d},\\
i k_ {x}\ tau e^ {i k_ {x} d} =\ kappa\ left (-T_ {I} e^ {-\ kappa d} +R_ {I I} e^ {\ kappa d}\ derecha).
\ end {reunido}\]

Esto parece más complicado de lo que realmente es. Si resolvemos para\(T_{I I} e^{-\kappa d}\) y\(R_{I I} e^{\kappa d}\) en términos de\(\tau e^{i k_{x} d}\), el resultado es\[T_{I I} c^{-\kappa d}=\frac{2 \kappa}{\kappa-i k_{x}} \tau c^{i k_{x} d}, \quad R_{I I} e^{\kappa d}=\frac{2 \kappa}{\kappa+i k_{x}} \tau c^{i k_{x} d} .\]

El punto importante es que los valores de los dos componentes de la onda, (11.75), at\(x = d\),\(T_{I I} e^{-\kappa d}\) y\(R_{I I} e^{-\kappa d}\), son más o menos del mismo tamaño. Estas dos cantidades no tienen ninguna dependencia exponencial de\(d\). Este hecho cualitativo no depende de los detalles de (11.76). Será cierto para cualquier condición límite razonable en\(x = d\).

Así, el coeficiente,\(R_{I I}\) de la onda “reflejada” (entre comillas porque es una onda exponencial real, no una onda viajera) debe ser menor que la onda “transmitida” por un factor de aproximadamente\(e^{2 \kappa d}\). Observe que esto justifica la afirmación, (11.67), de la condición límite al infinito. Como\(d \rightarrow \infty\), para cualquier física razonable en\(d\), la onda se convierte en un exponencial negativo puro.

En\(x = 0\), en general\(\kappa d\), el\(R_{I I}\) término en onda será completamente despreciable, y el\(T_{I I}\) término se producirá con algún coeficiente de orden 1, así como en el límite de reflexión interna total.

Así, lo que está sucediendo en las condiciones de límite para la tunelización se puede describir cualitativamente de la siguiente manera. La onda entrante para\(x < 0\) produce el\(e^{-\kappa x}\) término en la región\(0 \leq x \leq d\), con una mezcla exponencialmente pequeña de\(e^{\kappa x}\). Pero en\(x = d\), las dos partes de la onda exponencial son del mismo tamaño (ambas exponencialmente pequeñas), y pueden producir la onda transmitida.

La rápida dependencia exponencial de la onda transmitida\(d\) tiene algunas consecuencias interesantes. Implica, por ejemplo, que la onda reflejada también es muy sensible al valor de\(d\), para pequeños\(d\) (implica la conservación de energía\(|R|^{2}+|\tau|^{2}=1\)). Se puede ver esta rápida dependencia en el ejemplo de (11.10) poniendo el dedo en la superficie inferior del bloque de vidrio o pecera, donde se está reflejando la ola. ¡Verás una huella fantasmal! La razón es que las diminutas hendiduras en tu dedo están lo suficientemente alejadas del vaso que\(\kappa d\) es grande y la onda se refleja casi en su totalidad. Pero donde la carne se presiona fuertemente contra el vidrio, la onda se absorbe. Esta es una versión simple de un microscopio de tunelización.

Por último, antes de dejar el tema del túnel, consideremos qué sucede cuando bajamos la intensidad de la onda de luz en Figura\( 11.11\) para que veamos la dispersión de fotones individuales. Lo primero a tener en cuenta es que cada fotón es transmitido o reflejado. El significado de\(R\) y\(\tau\) en este caso es que el\(|R|^{2}\) y\(|\tau|^{2}\) son las probabilidades de reflexión y transmisión. No se puede predecir si algún fotón en particular va a pasar. En el mundo de la mecánica cuántica, solo se pueden predecir las probabilidades.

Lo segundo a tener en cuenta es que en la descripción de las partículas, todo el fenómeno de la tunelización es muy peculiar. Un fotón clásico, que llegaba al límite de la placa de vidrio a más del ángulo crítico, no podía entrar en absoluto en el aire. Estaría prohibido hacerlo por conservación de energía y conservación del\(y\) componente de impulso. ⁴ ¿Cómo puede pasar la partícula hacia\(x > d\) un lado si no puede existir para\(0 < x < d\)? Obviamente, en la física clásica, no puede. La tunelización es, por lo tanto, un fenómeno mecánico verdaderamente cuántico. La ola logra penetrar en la región prohibida, pero sólo en forma de una onda exponencial real, no una ola viajera. Es sólo para\(x < 0\) y\(x > d\), donde viajan las olas, que pueden ser interpretadas como partículas en cualquier cosa como el sentido clásico.

__________________

²\(\psi_{\pm}\) Aquí hemos definido para facilitar la discusión de las condiciones de contorno, a continuación.
³ Nótese que es la masa del electrón más que la masa del protón lo que es relevante, porque los electrones se mueven mucho más en los campos eléctricos.
⁴ El límite no cambia\(p_{y}\) del fotón, debido a la invarianza de traducción en la\(y\) dirección. Sin embargo, no hay razón para que el límite no pueda ejercer una fuerza en la\(x\) dirección y cambio\(p_{x}\) del fotón.