11.3: Placas Chladni

Figura\( 11.13\): Una placa Chladni.

Las placas Chladni son un ejemplo muy bonito e instructivo de un sistema oscilante bidimensional. Una placa Chladni es simplemente una placa metálica cuadrada que se acciona transversalmente en su centro. Se ilustra en la Figura\( 11.13\). El punto en el centro muestra dónde se impulsa la placa en la dirección transversal (fuera del plano del papel). El centro, que tomaremos para tener posición de equilibrio\(\vec{r} = 0\), se mueve hacia arriba y hacia abajo fuera del plano del papel a una frecuencia\(\omega\). Supongamos que el cuadrado se sienta en el\(x\) -\(y\) plano y tiene lado\(2L\), y llamar al desplazamiento transversal (en la\(z\) dirección)\[\psi(x, y, t) \quad \text { for } \quad|x|,|y| \leq L .\]

En principio se trata de un problema de oscilación forzada. Podríamos tomar la condición límite en el origen para ser\[\psi(0,0, t)=A \cos \omega t\]

y tratar de encontrar\(\psi\) en cualquier otro lugar.

Para encontrar\(\psi\), debemos conocer la condición de contorno en los bordes de la placa. Esto depende de los detalles de la física de la placa, porque hay varias formas en que la placa puede deformarse en respuesta a la fuerza impulsora. Sólo por simplicidad, asumiremos que la deformación dominante es la cizalla, ilustrada en la Figura\( 11.14\). Para este tipo de desplazamiento, para evitar una aceleración infinita, la pendiente de la placa debe ir a cero en el límite en la dirección perpendicular al límite, o en matemáticas,\[\hat{n} \cdot \vec{\nabla} \psi=0\]

en el borde, donde\(\hat{n}\) hay un vector unitario en el plano perpendicular al borde. En este caso,\[\left.\frac{\partial}{\partial x} \psi(x, y, t)\right|_{x=|L|}=\left.\frac{\partial}{\partial y} \psi(x, y, t)\right|_{y=|L|}=0 .\]

Si bien el caso general es más complicado que esto, utilizaremos (11.81) como ilustración. Lo instructivo de las placas Chladni, como veremos, no es lo que está pasando en los bordes, ¡sino lo que está pasando en el medio!

La solución general a este problema de oscilación forzada no es fácil de anotar. Sin embargo, nos interesan primordialmente las resonancias. Esos son los modos de oscilación libre de

Figura\( 11.14\): Cizalla.

la placa (sujeta a la condición límite (11.81)) que puede ser excitada por la fuerza impulsora. Estos serán aquellos modos que tengan valores distintos de cero del desplazamiento en el origen.

Los modos de oscilación libre relevantes de la placa tienen la forma ⁵\[\psi_{\left(n_{x}, n_{y}\right)}(x, y, t)=A \cos \frac{n_{x} \pi x}{L} \cos \frac{n_{y} \pi y}{L} \cos \omega t\]

con\[\omega^{2}=\omega_{0}^{2}\left(\vec{k}^{2}\right) \Rightarrow \omega^{2}=f\left(n_{x}^{2}+n_{y}^{2}\right) .\]

Si las frecuencias de estos modos fueran únicas, (11.82) sería toda la historia. Pero lo interesante de este sistema es que la simetría garantiza que hay degeneración —es decir, que si\(n_{x} \neq n_{y}\), hay dos modos con la misma frecuencia. Podemos obtener un modo físicamente equivalente intercambiando\(n_{x} \longleftrightarrow n_{y}\), porque esto solo corresponde a una\(90^{\circ}\) rotación de la placa, que no cambia en absoluto la física. Cuando tenemos modos degenerados, entonces las combinaciones lineales de ellos también son modos, como se muestra en (3.117). Así tenemos que preguntarnos ¿qué combinaciones lineales son excitadas por la fuerza impulsora? Otra forma de decir esto se resume en (11.83). La invarianza de rotación asegura que\(\omega^{2}\) depende sólo de\(n_{x}^{2}+n_{y}^{2}\).

En particular, es claro que la diferencia\[\psi_{\left(n_{x}, n_{y}\right)}^{-}(x, y, t)=A\left(\cos \frac{n_{x} \pi x}{L} \cos \frac{n_{y} \pi y}{L}-\cos \frac{n_{y} \pi x}{L} \cos \frac{n_{x} \pi y}{L}\right) \cos \omega t\]

se desvanece en el origen. ¡Sólo la suma se empareja a la fuerza impulsora! \[\psi_{\left(n_{x}, n_{y}\right)}^{+}(x, y, t)=A\left(\cos \frac{n_{x} \pi x}{L} \cos \frac{n_{y} \pi y}{L}+\cos \frac{n_{y} \pi x}{L} \cos \frac{n_{x} \pi y}{L}\right) \cos \omega t\]

Estos son los modos resonantes de una placa Chladni.

Una razón por la que esto es divertido es que es fácil de ver. Si excita la placa, y espolvorea arena sobre ella, la arena se acumula en las regiones donde la placa no se mueve — a lo largo de los nodos de desplazamiento donde\(\psi=0\). Así podemos obtener una imagen visual de los ceros de\(\psi\). Veamos algunos de estos modos (en orden de frecuencia creciente) para ver qué esperar.

El modo no\(\psi_{(0,0)}^{+}\) es interesante. Corresponde a todo el plato subiendo y bajando como una cuadra. Obviamente, la frecuencia correspondiente es 0, porque no hay fuerza restauradora. El primer modo interesante es\[\psi_{(1,0)}^{+}(x, y, t)=A\left(\cos \frac{\pi x}{L}+\cos \frac{\pi y}{L}\right) \cos \omega t .\]

Esto se desvanece por\[y=\pm L \pm x\]

así que el patrón de arena Chladni se parece al diagrama de la Figura\( 11.15\).

Figura\( 11.15\): El patrón Chladni para el modo\(\left(n_{x}, n_{y}\right)=(1,0)\).

El siguiente modo es\[\psi_{(1,1)}^{+}(x, y, t)=2 A \cos \frac{\pi x}{L} \cos \frac{\pi y}{L} \cos \omega t .\]

Debido a que este modo no es degenerado, no da lugar a un patrón muy interesante. Se desvanece en\[x=\pm \frac{L}{2} \quad \text { or } \quad y=\pm \frac{L}{2} ,\]

que da el patrón que se muestra en la Figura\( 11.16\). No consideraremos más de estos modos aburridos con\(n_{x} = n_{y}\).

El siguiente modo es\[\psi_{(2,0)}^{+}(x, y, t)=A\left(\cos \frac{2 \pi x}{L}+\cos \frac{2 \pi y}{L}\right) \cos \omega t ,\]

que se desvanece por\[y=\pm \frac{L}{2} \pm x \quad \text { or } \quad y=\pm \frac{3 L}{2} \pm x\]

por lo que el patrón se parece a la Figura\( 11.17\).

Luego viene\[\psi_{(2,1)}^{+}(x, y, t)=A\left(\cos \frac{\pi x}{L} \cos \frac{2 \pi y}{L}+\cos \frac{2 \pi x}{L} \cos \frac{\pi y}{L}\right) \cos \omega t .\]

Esto desaparece para\ [\ begin {reunió}
c_ {x}\ left (2 c_ {y} ^ {2} -1\ right) +c_ {y}\ left (2 c_ {x} ^ {2} -1\ right) =0\\
=\ left (c_ {x} +c_ {y}\ right)\ left (2 c_ {x} c_ {y} -1\ derecha) =0
\ fin {reunidos}\]

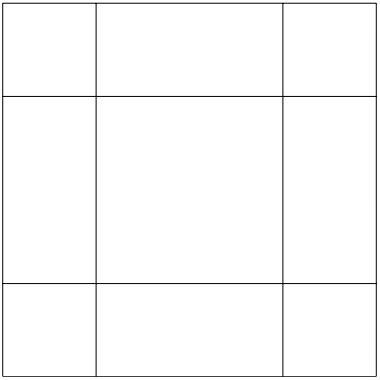
Figura\( 11.16\): El patrón Chladni para el modo (1,1).

Figura\( 11.17\): El patrón Chladni para el modo (2,0).

con\(c_{x} \equiv \cos (\pi x / L)\) y\(c_{y} \equiv \cos (\pi y / L)\) 9. El patrón se muestra en la figura 11.18.

Podríamos seguir, pero ya deberías tener la idea. Veamos un último modo:\[\psi_{(3,1)}^{+}(x, y, t)=A\left(\cos \frac{\pi x}{L} \cos \frac{3 \pi y}{L}+\cos \frac{3 \pi x}{L} \cos \frac{\pi y}{L}\right) \cos \omega t ,\]

Figura\( 11.18\): El patrón Chladni para el modo (2,1).

desapareciendo por\ [\ begin {reunió}
c_ {x}\ izquierda (4 c_ {y} ^ {3} -3 c_ {y}\ derecha) +c_ {y}\ izquierda (4 c_ {x} ^ {3} -c_ {x}\ derecha) =0\\
-c_ {x} c_ {y}\ izquierda (4 c_ {x} ^ {2} +4 c_ {y} ^ {2} -6\ derecha) -0
\ fin {reunidos}\]

con patrón mostrado en la figura 11.19.

Figura\( 11.19\): El patrón Chladni para el modo (3,1).

Moral: Cuando hay más de un modo con la misma frecuencia, ¡mira las combinaciones lineales para determinar cuáles están emocionados!

_________________

⁵ También hay modos proporcionales al pecado (nx + 1/2) πx/L y/o sin (ny + 1/2) πY/L, pero estos desaparecen en el origen y no son excitados por la fuerza impulsora.