2.5: Lema - El área de espacio-tiempo es invariante
- Page ID
- 126564
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Objetivos de aprendizaje
- Para demostrar a partir de los axiomas P1 - P6 que el área en el\(x - t\) plano es invariante
En esta sección demostramos a partir de los axiomas P1-P6 que el área en el\(x - t\) plano es invariante, es decir, no cambia entre marcos de referencia. Este resultado se utilizó en la Sección 1.3 para encontrar la forma de la métrica espacio-tiempo. Considera figura\(\PageIndex{1}\).
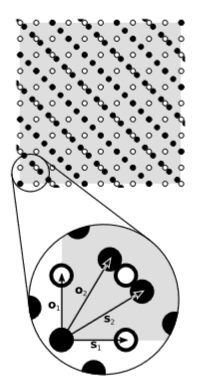
Los vectores\(\overrightarrow{o_1}\) y\(\overrightarrow{s_1}\) son ortogonales y tienen longitudes iguales medidas por un reloj y una regla (que se calibran en unidades tales que\(c = 1\), por ejemplo, segundos y luz-segundos). La celosía cuadrada de lunares blancos se obtiene de ellos por adición repetida. Al asumir que esta construcción de celosía es posible, estamos asumiendo implícitamente el postulado P2, planitud del espacio-tiempo.
Las mismas propiedades se mantienen para los vectores\(\overrightarrow{o_2}\) y\(\overrightarrow{s_2}\), que dan la celosía de puntos negros. Según se requiere, las dos celosías coinciden en sus diagonales de\(45\) grado. Ahora dentro de la\(10 × 10\) porción de la celosía blanca que se muestra con sombreado gris, tenemos un área de\(100\). En la misma región contamos alrededor\(100\) o puntos\(101\) negros —hay cierta ambigüedad por los puntos que se encuentran en el límite. La densidad de los puntos blancos y negros es de hecho exactamente igual, ya que se puede verificar con cualquier precisión deseada haciendo que la región sea lo suficientemente grande. Es decir, se dibuja el diagrama para que se conserve esa zona, que es lo que vamos a mostrar se requiere. Si fuera observador\(2\) más\(1\) que quien estaba dibujando el diagrama, presumiblemente ella elegiría dibujar los puntos negros en una celosía cuadrada y vectores\(\overrightarrow{o_2}\) y\(\overrightarrow{s_2}\) en ángulo recto. Esto requeriría vectores\(\overrightarrow{o_2}\) y\(\overrightarrow{s_2}\) que se abrieran en ángulo oblicuo y que la celosía blanca no fuera cuadrada.
Ahora supongamos que no habíamos hecho área conservada. ¿Y si una región que contiene puntos\(100\) blancos hubiera tenido\(200\) negros? El conteo de puntos es como definen el área los observadores, por lo que si esto sucediera, tendrían que estar de acuerdo en que un impulso al\(v\), de fotograma\(1\) a fotograma\(2\), duplicó el área de la región gris. Debido a que el espacio-tiempo es plano (P2) y homogéneo (P3), es posible tomar una forma geométrica inscrita en una determinada región del espacio-tiempo y moverlo, rotarlo o voltearlo. Y por isotropía del espacio (P3), un impulso de velocidad\(v\) es lo mismo que un giro de la dimensión espacial seguido de un\(-v\) impulso y otro giro. El área se conserva por un volteo, por lo que encontramos que un impulso por\(-v\), de cuadro\(2\) a cuadro\(1\), también dobla área. De esta manera, un\(+v\) impulso seguido de un\(-v\) impulso provocaría un cuadruplicado del área. Pero se cancela un par de potenciadores iguales y opuestos, por lo que esto es una contradicción. Concluimos que si estos principios de simetría se mantienen, entonces el área espacio-tiempo es la misma para dos observadores cualesquiera, por lo que es una invariante.
Puede parecer innecesariamente torpe que hayamos usado la idea de contar puntos en el argumento anterior, pero recuerde que nuestro principal uso de este resultado es derivar la forma de la métrica, y antes de que se encontrara la métrica, no teníamos sistema de medición para la relatividad, por lo que solo teníamos técnicas muy primitivas en nuestro eliminación.


