2.E: Fundaciones (Ejercicios)
- Page ID
- 126565
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q1
La sección 2.5 da un argumento de que el área espacio-tiempo es una invariante relativista. ¿Este argumento también es válido para la relatividad galilea?
Q2
La sección 2.5 da un argumento de que el área espacio-tiempo es una invariante relativista.
- Generalizar esto de\(1+1\) dimensiones a\(3+1\).
- Utilice este resultado para demostrar que no existe un efecto relativista de tracción de longitud a lo largo de un eje perpendicular a la velocidad.
Q3
El propósito de este problema es encontrar cómo cambia la dirección de un objeto físico como un palo bajo una transformación de Lorentz. La parte b del problema Q2 muestra que la contracción relativista de la longitud ocurre solo a lo largo del eje paralelo al movimiento. Por lo tanto, la generalización de la\(1 + 1\) transformación de Lorentz dimensional a\(2 + 1\) dimensiones consiste simplemente en aumentar la ecuación 1.4.1 en la sección 1.4 con\(y'=y\). Supongamos que un palo, en su propio marco de descanso, tiene un extremo con una línea de mundo\((\tau , 0, 0)\) y el otro con\((\tau , p, q)\), donde\(\tau\) es el momento adecuado del palo. Llama a estos fines\(A\) y\(B\). Es decir, tenemos un palo que va desde el origen hasta las coordenadas\((p, q)\) en el\((x, y)\) plano. Aplica una transformación de Lorentz para un impulso con velocidad\(v\) en la dirección x, y encuentra las ecuaciones de las líneas mundiales de los extremos del palo en las nuevas\((t', x', y')\) coordenadas. De acuerdo con la noción de simultaneidad de este nuevo marco, encontrar las coordenadas de\(B\) cuándo\(A\) está en\((t', x', y')= (0, 0, 0)\).
- En el caso especial donde\(q \neq 0\), recuperar el resultado\(1 + 1\) - dimensional para la contracción de longitud dado en la sección 1.3.
- Volviendo al caso general donde\(q \neq 0\),, considerar el ángulo\(\theta\) que hace el palo con el\(x\) eje, y el ángulo relacionado\(\theta ' \) que hace con el\(x'\) eje en el nuevo marco. Demostrar que\(tan(\theta ') = \gamma tan(\theta)\)
Q4
La sección 2.2 discute la idea de que un error bidimensional que vive en la superficie de una esfera podría decir que su espacio era curvo. La figura 2.2.2 en la sección 2.2 muestra una forma de decir, al detectar la dependencia de la trayectoria del transporte paralelo. Una técnica diferente sería buscar violaciones al teorema de Pitágoras. En la figura 2.E.1 siguiente, 1 es un diagrama que ilustra la prueba del teorema de Pitágoras en Elementos de Euclides (sección 2.2/ 2.3). Este diagrama es igualmente válido si la página se enrolla sobre un cilindro, 2, o se forma en una forma ondulada ondulada, 3. Este tipo de curvatura, que se puede lograr sin rasgar o arrugar la superficie, no son reales para el error. Simplemente son efectos secundarios de visualizar su universo bidimensional como si estuviera incrustado en una hipotética tercera dimensión —que no existe en ningún sentido que sea empíricamente verificable para el error. De las superficies curvas en la figura, solo la esfera, 4, tiene una curvatura que el insecto puede medir; el diagrama no se puede enlustrar sobre la esfera sin plegar o cortar y pegar. Si un ser bidimensional viviera sobre la superficie de un cono, ¿diría que su espacio era curvo, o no? ¿Qué tal una forma de silla de montar?
Q5
La discrepancia en el transporte paralelo que se muestra en la figura 2.2.2 en la sección 2.2 también puede interpretarse como una medida del defecto angular del triángulo\(d\), es decir, la cantidad\(S - \pi\) en que la suma de sus ángulos interiores\(S\) excede el valor euclidiano.
- La figura sugiere una manera sencilla de verificar que el defecto angular de un triángulo inscrito en una esfera depende del área. Muestra un gran triángulo equilátero que ha sido diseccionado en cuatro triángulos más pequeños, cada uno de los cuales es también aproximadamente equilátero. Demuéstralo\(D = 4d\), donde\(D\) está el defecto angular del triángulo grande y\(d\) el valor para uno de los cuatro más pequeños.
- Dado que la proporcionalidad al área se\(d = kA\) mantiene en general, encontrar algún triángulo en una esfera de radio\(R\) cuya área y defecto angular sean fáciles de calcular, y utilízalo para fijar la constante de proporcionalidad\(k\).
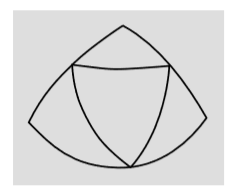
Observación: Un ser que vivía en una esfera podría medir\(d\) y\(A\) para algún triángulo e inferir\(R\), que es una medida de curvatura. La proporcionalidad del efecto al área del triángulo también implica que los efectos de la curvatura se vuelven despreciables en escalas suficientemente pequeñas. La analogía en la relatividad es que la relatividad especial es una aproximación válida a la relatividad general en regiones del espacio que son lo suficientemente pequeñas como para que la curvatura espacio-temporal se vuelva insignificante.