4.3: Momentum relativista

Objetivos de aprendizaje

• Explicar la relatividad y el impulso
• Conservación global del impulso

El vector de impulso de energía

La mecánica newtoniana tiene dos medidas diferentes de movimiento, energía cinética e impulso, y la relación entre ellas es no lineal, por ejemplo, duplicar el impulso de tu auto cuadruplica su energía cinética. Sin embargo, la mecánica no relativista no puede manejar partículas sin masa, que siempre son ultrarelativistas. Vimos en la Sección 4.1 que las partículas ultrarelativistas son “genéricas”, en el sentido de que no tienen propiedades mecánicas individuales que no sean una energía y una dirección de movimiento. Por lo tanto, la relación entre la energía cinética y el momento debe ser lineal para las partículas ultrarelativistas. Por ejemplo, duplicar la amplitud de una onda electromagnética cuadruplica tanto su densidad de energía, que depende de\(E^2\) y\(B^2\), como su densidad de momento, que va como\(E×B\).

¿Cómo podemos darle sentido a estas relaciones energía-impulso, que parecen adoptar dos formas completamente diferentes en los casos limitantes de velocidades muy bajas y muy altas?

El primer paso es darnos cuenta de que dado que la masa y la energía son equivalentes, obtendremos más una comparación de manzanas a manzanas si dejamos de hablar de la energía cinética de un objeto material y consideramos en cambio su energía total E, que incluye una contribución de su masa.

Figura\(\PageIndex{1}\): En el\(p-E\) plano, las partículas sin masa se encuentran en las dos diagonales, mientras que las partículas con masa se encuentran a la derecha.

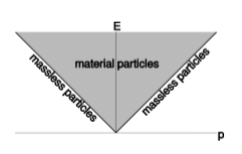
La figura\(\PageIndex{1}\) es una gráfica de energía versus impulso. En esta representación, las partículas sin masa, que tienen\(E \propto |p|\), se encuentran sobre dos líneas diagonales que conectan en el origen. Si nos gusta, podemos escoger unidades de tal manera que las pendientes de estas líneas sean más y menos uno. Las partículas de material se encuentran sobre estas líneas. Por ejemplo, un auto sentado en un estacionamiento tiene\(p = 0\) y\(E = m\).

Ahora bien, ¿qué sucede con un gráfico así cuando cambiamos a un fotograma o referencia diferente que está en movimiento con relación al fotograma original? Una partícula sin masa todavía tiene que actuar como una partícula sin masa, por lo que las diagonales simplemente se estiran o contraen a lo largo de sus propias longitudes. Una transformación que siempre lleva una línea a una línea es una transformación lineal, y si la transformación entre diferentes marcos de referencia preserva la linealidad de las líneas\(p = E\) y\(p = -E\), entonces es natural sospechar que en realidad es algún tipo de transformación lineal. De hecho la transformación debe ser lineal, porque la conservación de la energía y el impulso implican suma, y necesitamos que estas leyes sean válidas en todos los marcos de referencia. Pero ahora por el mismo razonamiento que en la sección 1.3, la transformación debe ser conservadora de área. Entonces tenemos los mismos tres casos a considerar que en la figura 1.1.10. Se descarta la versión “galileana” porque implicaría que las partículas mantienen la misma energía cuando cambiamos de fotogramas. (Esto es lo que pasaría si\(c\) fueran infinitos, de manera que el equivalente en masa\(E/c^2\) de una energía dada fuera cero, y por lo tanto se\(E\) interpretaría puramente como la masa.) Tampoco puede ser correcta la versión “rotacional”, porque no conserva las\(E = |p|\) diagonales. Nos quedamos con el tercer caso, que establece el siguiente hecho estéticamente atractivo:

Energía-impulso es un

Que un objeto aislado tenga ímpetu y masa-energía\(p\) y\(E\). Entonces el\(p-E\) plano se transforma de acuerdo exactamente con el mismo tipo de transformación de Lorentz que el\(x-t\) plano. Es decir,\((E,p_x,p_y,p_z)\) es un vector de cuatro dimensiones al igual que\((t,x,y,z)\).

Este es un resultado muy deseable. Si no fuera cierto, sería como tener que aprender diferentes reglas matemáticas para diferentes tipos de tres vectores en la mecánica newtoniana.

El único problema que queda por resolver es si la elección de unidades que da diagonales invariantes de\(45\) grado en el\(x-t\) plano es la misma que la elección de unidades que da tales diagonales en el\(p-E\) plano. Es decir, necesitamos establecer que el\(c\) que aplica\(x\) y\(t\) es igual a lo\(c'\) necesario para\(p\) y\(E\), es decir, que las escalas de velocidad de las dos gráficas se emparejen hacia arriba. Esto es cierto porque en el límite newtoniano, la masa-energía total\(E\) es esencialmente solo la masa de la partícula, y luego\(p/E \approx p/m \approx v\). Esto establece que las escalas de velocidad se emparejan a velocidades pequeñas, lo que implica que coinciden para todas las velocidades, ya que una velocidad grande, incluso una que se aproxima\(c\), se puede construir a partir de muchos pequeños incrementos. (Esto también establece que el exponente\(n\) definido sección 4.1 es igual a\(1\) como se reivindica.)

Supongamos que una partícula está en reposo. Entonces tiene\(p = 0\) y energía de masa\(E\) igual a su masa\(m\). Por lo tanto, el producto interno de sus\((E,p)\) cuatro vectores consigo mismo es igual\(m^2\). En otras palabras, la “magnitud” del cuatro vector energía-impulso es simplemente igual a la masa de la partícula. Si nos transformamos en un marco de referencia diferente, en el que\(p \neq 0\), el producto interno permanece igual. En símbolos,

\[m^2 = E^2 - p^2\]

o, en unidades con\(c \neq 1\),

\[(mc^2)^2 = E^2 - (pc)^2\]

Tomamos esto como la definición relativista de masa. Dado que la definición es un producto interno, que es un escalar, es el mismo en todos los marcos de referencia. (Algunos libros más antiguos utilizan una convención obsoleta de referirse a mγ como “masa” y m como “masa de descanso”).

Ejercicio\(\PageIndex{1}\)

Interpreta la ecuación m^2 = E^2 −p^2 en el caso donde\(m = 0\).

Una prueba de alta precisión de esta relación relativista fundamental fue realizada por Meyer et al. en 1963 mediante el estudio del movimiento de electrones en campos eléctricos y magnéticos estáticos. Definen la cantidad

\[Y^2 = \frac{E^2}{m^2 + p^2}\]

que según la relatividad especial debe ser igual\(1\). Sus resultados, tabulados en la barra lateral, muestran una excelente concordancia con la teoría.

Ejemplo\(\PageIndex{1}\): Mass of two light waves

Que sea el impulso de cierta onda de luz\((p_t,p_x) = (E,E)\), y que otra onda de este tipo tenga impulso\((E,-E)\). El impulso total es\((2E,0)\). Así este par de partículas sin masa tiene una masa colectiva de\(2E\). Este es un ejemplo de la no aditividad de la masa relativista.

Invariantes de colisión

El ejemplo\(\PageIndex{1}\) muestra que la masa no es aditiva, ni es una medida de la “cantidad de materia”. De manera más general, supongamos que tenemos una colisión entre dos objetos, que podrían ser dos autos o dos núcleos en un acelerador de partículas. La conservación del impulso (espacial) dicta que no toda la energía esté disponible para romper parabrisas o crear rayos gamma. Por ejemplo, un marciano que observaba un fender-bender de un estacionamiento a través de un potente telescopio diría que ambos autos iban tan rápido como los aviones de combate, debido a la rotación de la tierra, pero esto no hace que la explosión sea más fuerte. Para evitar ser engañados por estas distracciones dependientes del marco, solo podemos concentrarnos en cantidades que son escalares. Para una colisión de dos cuerpos, hay tres escalares de este tipo que podemos construir:\(P_{1}^{2}\),\(P_{2}^{2}\), y\(P_1 \cdot P_2\). (La notación\(a^2\) es simplemente una abreviatura de\(a \cdot a\).) Estos son conocidos como los invariantes de colisión. Los dos primeros de estos son simplemente las masas cuadradas de las partículas individuales.

Ahora considere el marco del centro de masa, es decir, el marco en el que el impulso total tiene una parte parecida a un espacio cero. En este marco, el vector energía-impulso total es de la forma\((E_{cm},0)\), correspondiente a una masa\(M = E_{cm}\). Toda esta energía está disponible para hacer una explosión. Si estuviéramos colisionando partículas en un acelerador para producir nuevas partículas, esta colisión sería apenas energía suficiente para crear una sola partícula de masa\(M\), si las dos partículas entrantes fueran aniquiladas en el proceso. Esta energía del centro de masa se puede expresar en términos de los invariantes de colisión como

\[\begin{align} M^2 &= (P_1 + P_2)^2 + P_{1}^{2} + P_{2}^{2} + 2P_1 \cdot P_2 \\[5pt] &= m_{1}^{2} + m_{2}^{2} + 2P_1 \cdot P_2 \end{align}\]

Esta es una relación no lineal, y la tercera colisión invariante nos\(P_1 \cdot P_2\) dice cómo se desarrolla la no linealidad basada en las direcciones relativas del movimiento. Los dos vectores de impulso son tanto temporales como orientados al futuro, así que por la igualdad del triángulo invertido (sección 1.5) tenemos

\[M \geq m_1 + m_2\]

Algunos ejemplos que involucran impulso

Ejemplo\(\PageIndex{2}\): Finding velocity given energy and momentum

Si sabemos que una partícula tiene masa-energía\(E\) e impulso\(p\) (lo que implica también el conocimiento de su masa m), ¿cuál es su velocidad?

Solución

En el marco de reposo de la partícula tiene una línea mundial que apunta hacia arriba en un diagrama de espacio-tiempo, y su vector de impulso\(p\) también apunta hacia arriba en el\(p-E\) plano. Dado que los vectores de desplazamiento y los vectores de impulso se transforman de acuerdo con las mismas reglas, este paralelismo también se mantendrá en otros marcos. Por lo tanto, en un marco arbitrariamente elegido, el vector\(p = (E,p)\) se encuentra a lo largo de una línea cuya pendiente inversa\(v = p/E\) da la velocidad.

Como un control de nuestro resultado, miramos su comportamiento limitante. En el límite newtoniano, la masa-energía\(E\) se debe casi todo a la masa, así que tenemos\(v \approx p/m\), el resultado newtoniano. En el límite opuesto del movimiento ultrarelativista, con\(E \gg m\), la definición de masa\(m^2 = E^2 - p^2\) da\(E \approx |p|\), y tenemos\(|v| \approx 1\), lo que también es correcto.

Ejemplo\(\PageIndex{3}\): Light rays don’t interact

Observamos que cuando dos rayos de luz cruzan, continúan uno a través del otro sin rebotar como objetos materiales. Este comportamiento se deriva directamente de la conservación del impulso energético.

Dos vectores cualesquiera pueden estar contenidos en un solo plano, así que podemos elegir nuestras coordenadas para que ambos rayos hayan desaparecido\(p_z\). Al elegir el estado de movimiento de nuestro sistema de coordenadas apropiadamente, también podemos realizar\(p_y = 0\), de manera que la colisión se realice a lo largo de una sola línea paralela al\(x\) eje -eje. Ya que solo\(p_x\) es distinto de cero, lo escribimos simplemente como\(p\). En el\(p-E\) plano resultante, hay dos posibilidades: o los rayos se encuentran ambos a lo largo de la misma diagonal, o se encuentran a lo largo de diferentes diagonales. Si se encuentran a lo largo de la misma diagonal, entonces no puede haber colisión, porque los dos rayos se mueven ambos en la misma dirección a la misma velocidad\(c\), y el posterior nunca alcanzará al líder.

Ahora supongamos que se encuentran a lo largo de diferentes diagonales. Agregamos sus vectores de energía-impulso para obtener su impulso energético total, que se ubicará en la zona gris de la figura\(\PageIndex{1}\). Es decir, un par de rayos de luz tomados como un solo sistema actúan como un objeto material con una masa distinta de cero. Por una transformación de Lorentz, siempre podemos encontrar un marco en el que este vector total de energía-impulso se encuentre a lo largo del\(E\) eje. Este es un marco en el que se cancelan los momentos de los dos rayos, y tenemos una colisión frontal simétrica entre dos rayos de igual energía. Es el marco del “centro de masa”, aunque ninguno de los dos objetos tiene masa individual. Por conveniencia, supongamos que se eligió el sistema de\(x-y-z\) coordenadas para que su origen estuviera en reposo en este marco.

Dado que la colisión ocurre a lo largo\(x\) del eje -eje, por simetría no es posible que los rayos posteriores a la colisión se aparten\(x\) del eje -eje; pues si lo hicieran, entonces no habría nada que determine la orientación del plano en el que emergieron. ¹ Por lo tanto, estamos justificados en continuar utilizando el mismo\(p_x-E\) plano para analizar los cuatro vectores de los rayos después de la colisión.

Ejemplo\(\PageIndex{4}\): Compton scattering

Figura\(\PageIndex{2}\): 1. El borde Compton se encuentra en la energía depositada por los rayos gamma que se dispersan a 180 grados a partir de un electrón. La colisión en el marco del laboratorio. 3. La misma colisión en el marco del centro de masa.

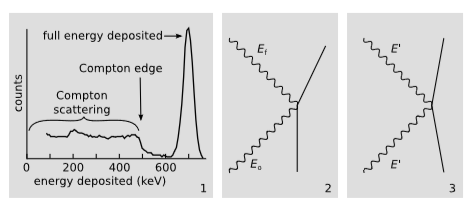
La Figura\(\PageIndex{2}\) (1) es un histograma de rayos gamma emitidos por una\(^{137}\textrm{Cs}\) fuente y registrados por un detector de centelleo de NaI. Este tipo de detector, a diferencia de un contador Geiger-Muller, da un pulso cuya altura es proporcional a la energía de la radiación. Alrededor de la mitad de los rayos gamma hacen lo que nos gustaría que hicieran en un detector: depositan toda su energía\(662\: keV\) en el detector, dando como resultado un pico prominente en el histograma. La otra mitad, sin embargo, interactúa a través de un proceso llamado dispersión de Compton, en el que chocan con uno de los electrones pero emergen de la colisión aún conservando parte de su energía, con la que pueden escapar del detector. La cantidad de energía depositada en el detector depende únicamente de la cinemática de bola de billar de la colisión, y se puede determinar a partir de la conservación de energía-momento basado en el ángulo de dispersión. La dispersión hacia adelante en\(0\) grados no es interacción en absoluto, y no deposita energía, mientras que la dispersión en\(180\) grados deposita la máxima energía posible si la única interacción dentro del detector es una única dispersión Compton. Analizaremos la dispersión\(180\) -grado, ya que puede abordarse en\(1+1\) dimensiones.

La figura\(\PageIndex{2}\) (2) muestra la colisión en el marco de laboratorio, donde el electrón está inicialmente en reposo. Como es convencional en este tipo de diagrama, la línea mundial del fotón se muestra como una línea ondulada; los meneos son solo una decoración, y la línea mundial real consta de dos segmentos de línea. El fotón ingresa al detector con toda la energía\(E_o = 662\: keV\) y sale con una energía más pequeña\(E_f\). La diferencia\(E_o - E_f\) es lo que medirá el detector, aportando un conteo al borde Compton. En el marco de laboratorio, el vector de impulso inicial total es\(p = (E_o + m,E_o)\), con el componente temporal que representa la masa-energía total. Debido a que el fotón es sin masa, su impulso\(p_x = E_o\) es igual a su energía.

\(v\)Sea la velocidad del marco de centro de masa,\(e/3\), relativo al marco de laboratorio. Usando el resultado del ejemplo\(\PageIndex{2}\), encontramos

\[v = \frac{E_o}{E_o + m}\]

Para facilitar la escritura definimos

\[\alpha = E_o/m\]

para que

\[v = \frac{\alpha }{1 + \alpha }\]

La transformación del marco de laboratorio al cuadro de c.m. Doppler desplaza la energía del fotón incidente a

\[E' = D(-v)E_o\]

La colisión invierte la parte espacial del vector energía-impulso del fotón mientras deja su energía igual. La transformación de nuevo en el marco de laboratorio da

\[E_f = D(-v)E' = D(-v)^2E_o = \frac{E_o}{1 + 2\alpha }\]

(Esto también se puede reescribir usando la relación mecánica cuántica\(E = hc/λ\) para dar la forma compacta)\(λ_f - λ_o = 2hc/m\). El resultado final para la energía del borde Compton es

\[E_o - E_f = \frac{E_o}{1 + \tfrac{1}{2\alpha }}\]

en buen acuerdo con la figura\(\PageIndex{2}\).

Ejemplo\(\PageIndex{5}\): Pair production requires matter

El Ejemplo 4.2.1 discutió la aniquilación de un electrón y un positrón en dos rayos gamma, lo que es un ejemplo de convertir la materia en energía pura. Un ejemplo opuesto es la producción de pares, un proceso en el que desaparece un rayo gamma, y su energía va a crear un electrón y un positrón.

La producción de pares no puede ocurrir en el vacío. Por ejemplo, los rayos gamma de agujeros negros distantes pueden viajar a través del espacio vacío durante miles de años antes de ser detectados en la tierra, y no se convierten en pares electrón-positrón antes de que puedan llegar hasta aquí. La producción por pares sólo puede ocurrir en presencia de materia. Cuando el plomo se usa como blindaje contra los rayos gamma, una de las formas en que los rayos gamma se pueden detener en el plomo es mediante la producción de pares.

Para ver por qué la producción de pares está prohibida en un vacío, considere el proceso en el marco de referencia en el que el par electrón-positrón tiene un impulso total cero. En este marco, el rayo gamma tendría que haber tenido impulso cero, pero un rayo gamma con impulso cero también debe tener cero energía. Esto significa que se ha violado la conservación del vector momentum: el componente timelike del momentum es la masa-energía, y ha aumentado desde\(0\) el estado inicial hasta al menos\(2mc^2\) en el estado final.

Las partículas sin masa viajan a\(c\)

Las partículas sin masa siempre viajan a\(c(= 1)\). Por suponer que una partícula sin masa tenía\(|v| < 1\) en el marco de algún observador. Entonces algún otro observador podría estar en reposo relativo a la partícula. En tal marco, el impulso de la partícula\(p\) es cero por simetría, ya que no hay dirección preferida para ella. Entonces también\(E^2 = p^2 + m^2\) es cero, así que todo el vector energía-impulso de la partícula es cero. Pero un vector que se desvanece en un fotograma también se desvanece en todos los demás fotogramas. Eso significa que estamos hablando de una partícula que no puede sufrir dispersión, emisión o absorción, y por lo tanto es indetectable por cualquier experimento. Esto es físicamente inaceptable porque no consideramos que los fenómenos (por ejemplo, las hadas invisibles) sean de interés físico si son indetectables incluso en principio.

¿Qué pasa con el caso de una partícula material, es decir, una que tiene masa? Como ya tenemos una ecuación\(E = mγ\) para la energía de una partícula material en términos de su velocidad, podemos encontrar una ecuación similar para el impulso,

\[\begin{align} p &= \sqrt{E^2 - m^2} \nonumber \\[5pt] &= m\sqrt{\gamma ^2 - 1} \nonumber \\[5pt] &= m\sqrt{\frac{1}{1 - v^2} - 1} \nonumber \\[5pt] &= m\gamma v \label{rel momentum} \end{align}\]

(una relación que es útil por derecho propio, y que ha sido verificada experimentalmente, Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Dos pruebas tempranas de alta precisión de la ecuación relativista\(p = mγv\) para el momento de una partícula material. Graficar\(p/m\) en lugar de\(p\) permitir que los datos de electrones y protones se coloquen en la misma gráfica. Las barras de error muy pequeñas para el punto de datos de Zrelov están representadas por la altura del rectángulo negro.

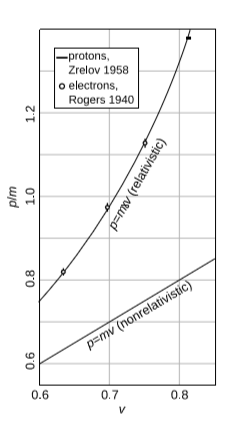
A medida que una partícula material se acerca cada vez más\(c\), su impulso se acerca al infinito, de manera que se requeriría una fuerza infinita para alcanzar\(c\).

En resumen, las partículas sin masa siempre se mueven hacia\(v = c\), mientras que las masivas siempre se mueven hacia\(v < c\).

Tenga en cuenta que la ecuación\(p = mγv\) (Ecuación\ ref {rel momentum}) no es lo suficientemente general como para servir como definición de impulso, ya que se convierte en una forma indeterminada en el límite\(m \rightarrow 0\).

Ejemplo\(\PageIndex{6}\): No half-life for massless particles

Ejemplo\(\PageIndex{7}\): Constraints on polarization

Observamos que las ondas electromagnéticas son siempre polarizadas transversalmente, nunca longitudinalmente. Tal restricción sólo puede aplicarse a una onda que se propaga en\(c\). Si se aplicara a una onda que se propagaba a menos de\(c\), podríamos movernos a un marco de referencia en el que la ola estuviera en reposo. En este marco, todas las direcciones en el espacio serían equivalentes, y no habría forma de decidir qué direcciones de polarización deberían permitirse.

Evidencia de qué partículas son sin masa

¿Cuáles de las partículas fundamentales son sin masa y cuáles no? Esto solo se puede determinar empíricamente, y tenemos al menos un ejemplo, el neutrino, que antes se pensaba que era sin masa pero que ahora se cree que es masivo. Para más información sobre el neutrino, véase la sección 4.7. En la presente sección se discuten los límites de las masas del fotón y del gravitón. ⁵ Omitimos una discusión sobre el gluón, lo que se complicaría por el hecho de que el gluón nunca se observa como una partícula libre o como un campo clásico. Esta sección se puede omitir sin pérdida de continuidad.

Algunos lectores pueden exclamar en este punto que por supuesto los fotones deben ser sin masa, porque la luz tiene que viajar a la velocidad de la luz. Pero debe quedar claro de la presentación anterior que la\(c\) en relatividad no debe interpretarse como la velocidad de la luz, sino como una especie de factor de conversión entre el espacio y el tiempo. Si los fotones tienen una masa pequeña pero no desaparecida, la relatividad no tiene una estaca impulsada a través de su corazón.

Si queremos probar si el fotón es sin masa, la técnica más sencilla parecería ser medir su tiempo de vuelo a medida que recorre cierta distancia, y ver si va más lento que\(c\). Aquí hay una dificultad porque nuestros métodos para medir grandes distancias, por ejemplo, GPS, generalmente asumen que la luz viaja a\(c\). Sin embargo, si el fotón tiene algo de masa, entonces su velocidad debería depender de su energía, por lo que podemos probar si la velocidad de un fotón depende de su energía. Desde la mecánica cuántica, esto está relacionado con su frecuencia por\(E = hf\), por lo que esencialmente estamos probando si la velocidad de la luz en un vacío depende de la frecuencia. Actualmente las mejores pruebas experimentales de la invarianza de la velocidad de la luz con respecto a la longitud de onda provienen de observaciones astronómicas de ráfagas de rayos gamma, que son emanaciones repentinas de fotones de alta energía, que se cree que se originan a partir de una explosión de supernova en otra galaxia. Una de esas observaciones, en 2009, ⁶ fotones recolectados de dicha explosión, con una duración de\(2\) segundos, lo que indica que el tiempo de propagación de todos los fotones difería en no más de\(2\) segundos de un tiempo total en vuelo del orden de diez mil millones de años, o aproximadamente una parte en \(10^{17}\)!

Figura\(\PageIndex{4}\): La concepción de un artista de un estallido de rayos gamma, resultante de una explosión de supernova.

Resulta, sin embargo, que los límites a la masa del fotón impuestos por las mediciones del tiempo de vuelo pueden mejorarse en muchos órdenes de magnitud utilizando otros métodos. En el modelo estándar de física de partículas, las fuerzas se transmiten por el intercambio de partículas. Aquí nos concentraremos en las fuerzas estáticas. Una fuerza electrostática es transmitida por el intercambio de fotones, y una fuerza gravitacional estática por el intercambio de gravitones. La gravedad no forma parte del modelo estándar de la física de partículas, y los gravitones individuales no pueden ser detectados directamente por ninguna tecnología previsible, ⁷ pero hay razones fundamentales para creer que deben existir, y en cualquier caso nuestra discusión es matemáticamente idéntica para la gravedad y electromagnetismo. Por lo tanto, discutiremos los campos electromagnéticos y luego anotaremos los resultados correspondientes para la gravedad.

Si imaginamos el campo que rodea una carga puntual estacionaria como un enjambre de fotones, entonces la primera pregunta que se nos ocurre es cuál es la fuente de la energía necesaria para crearlos. El argumento estándar de ondulación manual es el siguiente. Además de la forma habitual de energía momentánea del principio de incertidumbre de Heisenberg\(\Delta p \Delta x \overset{> }{\sim } h\), existe una forma energía-tiempo\(\Delta E \Delta t \overset{> }{\sim } h\). Esto parece obvio por analogía cuando consideramos que relativisticamente, la energía y el impulso son diferentes partes del cuatro vector energía-impulso, y de igual manera para el tiempo y la posición. Podemos interpretar esto en el sentido de que es posible, por cortos periodos de tiempo, engañar a la ley de conservación de la energía. Podemos robar un poco de energía pero luego devolverla de inmediato, siempre y cuando la duración del préstamo no sea más que aproximadamente\(t \sim h/E\). Durante este tiempo, una partícula virtual puede recorrer una distancia de no más de\(\sim hc/E\). Ahora para una partícula sin masa, esta energía puede ser tan pequeña como se desee, por lo que la fuerza puede llegar a distancias arbitrariamente grandes. Pero para una partícula masiva, tenemos la relación relativista\(E^2 - p^2 = m^2\), que requiere\(E ≥ m\), o\(E ≥ mc^2\) en unidades SI. Esta energía mínima corresponde a un rango máximo\(\sim h/mc\). En general, esperamos que el campo portado por una partícula masiva se caiga más rápidamente con la distancia que el campo de una partícula sin masa, y esperamos que esta caída sea parametrizada de alguna manera por una escala de longitud\(h/mc\).

¿Cómo esperaríamos que esto se desarrollara en la teoría clásica de los campos electromagnéticos?

Figura\(\PageIndex{5}\): Líneas de campo de una carga puntual. Las observaciones dentro de la pequeña región indicada por una caja permiten determinar qué tan lejos está la carga. 2. Líneas de campo de una placa de condensador infinita, según electromagnetismo estándar. Las observaciones dentro de la casilla no dan información sobre qué tan lejos está el cargo. 3. Una violación a la ley de Gauss.

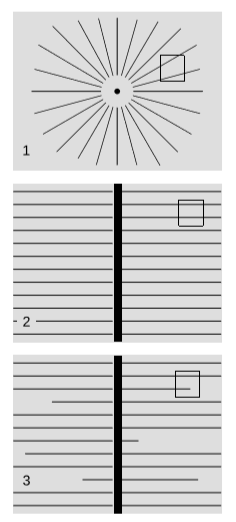
Considera una carga puntual, figura\(\PageIndex{5}\) (1). Sus líneas de campo son rectas, y se extienden en todas direcciones, por lo que mediante observaciones de cualquier región del espacio, podemos trazar las líneas hacia atrás para ver dónde se habrían intersectado. Eso es lo lejos que está de nuestra región del espacio a la carga. Este es un tipo de medición de paralaje. En el caso de la gravedad, esto es exactamente lo que hizo Eratóstenes para medir el radio de la tierra.

Pero ahora consideremos el caso de una placa de condensador infinita, plana con alguna carga sobre ella, figura\(\PageIndex{5}\) (2). Las líneas de campo no se extienden, por lo que el método de paralaje no funciona. Si examinamos el campo en alguna pequeña región del espacio, no debería haber forma de determinar la distancia a la placa del condensador. Si creemos en la ley de Gauss, entonces la solución es simple: el campo es constante tanto en magnitud como en dirección, así que aunque nos dice la dirección del punto más cercano en el plato, no nos dice nada sobre la distancia a ese punto.

Pero si el fotón es masivo, esperamos que los campos caigan más rápidamente con la distancia de lo que lo harían según la teoría estándar. En este ejemplo, la teoría estándar dice que el campo no disminuye en absoluto con la distancia, por lo que para un fotón masivo esperamos que sí se caiga. Esto violará la ley de Gauss, pero aún esperamos que la distancia a la placa no sea determinable mediante el examen de una pequeña región del espacio: si las ecuaciones de campo son lineales, entonces un campo con una intensidad dada podría ser de una placa de condensador cercana con una densidad de carga pequeña, o una más distante con más cargo.

Si estamos dispuestos a violar la ley de Gauss, entonces podemos hacer que las líneas de campo simplemente terminen en el espacio vacío, figura\(\PageIndex{1}\) (3), y esto hará que la fuerza de campo disminuya. A medida que atravesamos una pequeña distancia\(dx\), alejándonos de la placa, alguna fracción de las líneas de campo debe terminar, lo que lleva a una reducción fraccional correspondiente\(dE/E\) en la intensidad del campo. La relación\(\frac{\tfrac{dE}{E}}{dx}\) debe ser constante, y esto sólo puede suceder si tenemos\(E \propto e^{-\mu x}\), donde\(µ\) es una constante con unidades de longitud inversa. (En el otro lado de la placa, donde\(x\) es negativo, tenemos\(+µx\) dentro de lo exponencial.) Por las razones discutidas anteriormente, en realidad esperamos que\(µ\) sea igual\(mc/h\) multiplicado por una constante sin unidad de unidad de orden. De hecho, se puede demostrar que la constante sin unidad es un factor de\(2π\), por lo que\(µ\) simplemente la masa, expresada en unidades donde ambos\(c\) e\(\hbar\) iguales\(1\).

Dado que el campo de una placa de condensador es igual a la superposición de los campos de todas las cargas distribuidas uniformemente sobre ella, nuestro resultado de que el campo del condensador se cae de cierta manera nos dice algo correspondiente sobre el campo de una carga puntual. Esperamos que el campo de una carga puntual\(q\) sea

\[E = kq\frac{e^{-\mu r}}{r^2}\]

donde se recupera la ley de Coulomb en el caso\(µ = 0\). Esta forma fue inferida originalmente por Yukawa para las fuerzas nucleares, que realmente tienen un alcance finito.

Ahora tenemos una forma extraordinariamente sensible de poner un límite a las masas del fotón y gravitón. Aunque\(µ\) sea muy pequeño, podemos hacer observaciones en escalas de distancia muy grandes, y las fuerzas estáticas deberían caer exponencialmente. En el caso de las fuerzas gravitacionales, observamos que la gravedad sí opera, sin atenuación Yukawastyle detectable, en escalas comparables al tamaño del universo observable, del orden de miles de millones de años luz. Esto corresponde a un límite en la masa del gravitón de\(\sim 10^{-69}\: kg\) — ¡seguramente la escala de masa más pequeña que jamás haya sido sondeada por los seres humanos! Las mediciones del campo magnético de Júpiter por la sonda espacial Pioneer 10 limitan la masa del fotón a no más de aproximadamente\(8×10{-52}\: kg\), lo que es casi igual de impresionante.

Aunque los límites más estrechos de hoy provienen de mediciones de sistemas solares y cosmológicas, históricamente se llevaron a cabo algunos experimentos de mesa muy precisos. Los experimentos de laboratorio siempre son deseables en tales casos porque las condiciones pueden controlarse y los experimentos pueden replicarse.

No hay conservación global del impulso energético en la relatividad general

Si lees el capítulo 2, sabes que la distinción entre la relatividad especial y la general se define por la flotabilidad del espacio-tiempo, y esa flatness se define a su vez por la independencia del camino del transporte paralelo. Mientras que la energía es un escalar en la mecánica newtoniana, en la relatividad es el componente temporal de un vector. Por lo tanto, se deduce que en general la relatividad no debemos esperar tener una conservación global de la energía. Para una ley de conservación es una afirmación de que cuando sumamos una cierta cantidad, el total tiene un valor constante. Pero si el espacio-tiempo es curvo, entonces no hay una forma natural, definida de manera única, de comparar vectores que se definen en diferentes lugares del espacio-tiempo. Podríamos transportar en paralelo uno sobre otro, pero el resultado dependería del camino por el que elegimos transportarlo. Por razones similares, no debemos esperar una conservación global del impulso.

Esta es la respuesta a una pregunta frecuente sobre cosmología. Desde 1998 sabemos que la expansión del universo se está acelerando, en lugar de desacelerar como habríamos esperado debido a la atracción gravitacional. ¿Cuál es la fuente de la energía cinética cada vez mayor de todas esas galaxias? La pregunta asume que la energía debe conservarse en escalas cosmológicas, pero eso simplemente no es así.

Sin embargo, la relatividad general se reduce a relatividad especial en escalas lo suficientemente pequeñas como para hacer que los efectos de curvatura sean insignificantes. Por lo tanto, sigue siendo válido esperar que la conservación de la energía y el impulso se mantengan localmente, como se supone, por ejemplo, en el análisis de la dispersión de Compton en el ejemplo\(\PageIndex{4}\), y se verificó en innumerables experimentos.

Referencias

¹ En la mecánica cuántica, aquí hay un resquicio. La mecánica cuántica permite ciertos tipos de aleatoriedad, de manera que la simetría se puede romper dejando que los rayos salientes se observen en un plano con cierta orientación aleatoria.

² Aquí hay una segunda laguna, que es que un rayo de luz es en realidad una onda, y una onda tiene otras propiedades además de la energía y el impulso. Tiene una longitud de onda, y algunas ondas también tienen una propiedad llamada polarización. Como analogía mecánica para la polarización, considere una cuerda estirada tensa. Las vibraciones de lado a lado pueden propagarse a lo largo de la cuerda, y estas vibraciones pueden ocurrir en cualquier plano que coincida con la cuerda. La orientación de este plano se conoce como la polarización de la onda. Volviendo al caso de los rayos de luz colisionantes, es posible tener colisiones no triviales en el sentido de que los rayos podrían afectar las longitudes de onda y polarizaciones de los demás. Aunque esto en realidad no sucede con ondas de luz no cuánticas-mecánicas, puede ocurrir con otros tipos de ondas; véase, por ejemplo, Hu et al., arxiv.org/abs/hep-ph/9502276, figura 2. El título del ejemplo 4.3.3 sólo es válido si se toma un “rayo” como algo que carece de estructura de onda. La naturaleza ondulada de la luz no es evidente en la vida cotidiana a partir de observaciones con aparatos como reflashlights, espejos y anteojos, por lo que esperamos que el resultado se mantenga en esas circunstancias, y lo hace. Por ejemplo, los haces de luz de luz pasan a través de una antera sin interactuar.

³ Véase Fiore y Modanese, arxiv.org/abs/hep-th/9508018, y http://physics.stackexchange.com/questions/12488/ desintegración de partículas masivas. Si tal proceso existe, entonces la invarianza de Lorentz requiere que su escala de tiempo sea proporcional a la energía de la partícula. Se puede argumentar que los gluones, que son sin masa, de hecho sufren descomposición en gluones menos energéticos, pero la interpretación es ambigua porque nunca observamos los gluones como partículas libres, por lo que no podemos simplemente capturar uno en una caja y verlo traquetear por dentro hasta que decae.

⁴ Para una revisión en profundidad de este tema, consulte Goldhaber y Nieto, “Límites de masas de fotones y gravitones”, http://arxiv.org/abs/0809.1003.

⁵ http://arxiv.org/abs/0908.1832

⁶ Rothman y Boughn, “¿Se pueden detectar gravitones? ,” http://arxiv.org/ abs/gr-qc/0601043