4.2: E=mc²

Objetivos de aprendizaje

• Teoría relativista de la gravedad y$E = mc^2$ explicada

Ahora conocemos la expresión relativista de la energía cinética en el caso limitante de una partícula ultrarelativista: su energía es proporcional al “factor de estiramiento”$D$ de la transformación de Lorentz. ¿Qué pasa con los casos intermedios, como$v = c/2$?

Figura$\PageIndex{1}$: La cerilla está encendida dentro de la campana. Se quema, y la energía se escapa de la jarra en forma de luz. Después de que deja de arder, todos los mismos átomos siguen en el frasco: ninguno ha entrado ni escapado. La cifra muestra el resultado esperado antes de la relatividad, que fue que la masa medida en la balanza permanecería exactamente igual. Esto no es lo que sucede en la realidad.

Cuando nos vemos obligados a jugar con una teoría consagrada, nuestro primer instinto siempre debe ser jugar de la manera más conservadora posible. Aunque nos hemos visto obligados a admitir que la energía cinética no varía como$v^2/2$ a velocidades relativistas, lo siguiente más conservador que podríamos hacer sería suponer que el único cambio necesario es reemplazar el factor de$v^2/2$ en la expresión no relativista por energía cinética por algún otro función, que tendría que actuar como$D$ o$1/D$ para$v \rightarrow \pm c$. Sospecho que esto es lo que pensó Einstein cuando completó su trabajo original sobre la relatividad en 1905, porque no fue hasta más tarde ese año que publicó un segundo artículo que demostraba que esto todavía no era un cambio suficiente para producir una teoría de trabajo. Ahora sabemos que hay algo más que hay que cambiar sobre la física prerelativista, y esta es la suposición de que la masa es sólo una propiedad de partículas materiales como los átomos (figura$\PageIndex{1}$). Llama a esto la “hipótesis de solo los atomos”.

Ahora que conocemos la forma relativista correcta de encontrar la energía de un rayo de luz, resulta que podemos usar eso para encontrar lo que originalmente buscábamos, que era la energía de un objeto material. La siguiente discusión sigue de cerca la de Einstein.

Supongamos que un objeto material$O$ de masa$m_o$, inicialmente en reposo en un determinado marco$A$, emite dos rayos de luz (o cualquier otro tipo de partículas ultrarelativistas), cada uno con energía$E/2$. Por conservación de energía, el objeto debe haber perdido una cantidad de energía igual a$E$. Por simetría,$O$ permanece en reposo.

Ahora cambiamos a un marco de referencia diferente$B$ moviéndose a cierta velocidad arbitraria correspondiente a un factor de estiramiento$D$. El cambio de marcos significa que estamos persiguiendo un rayo, de modo que su energía se reduce a$\left ( \frac{E}{2} \right )D^{-1}$, mientras huye del otro, cuya energía se impulsa a$\left ( \frac{E}{2} \right )D$. En marco$B$, como en$A$,$O$ conserva la misma velocidad después de la emisión de la luz. Pero observadores en marcos$A$ y en$B$ desacuerdo sobre cuánta energía$O$ ha perdido, siendo la discrepancia

$$E\left [ \frac{1}{2} (D + D^{-1})-1\right ]$$

Esto se puede reescribir usando la identidad [2] de la sección 3.6 como

$$E(\gamma -1)$$

Consideremos el caso donde la velocidad de B relativa a A es pequeña. Usando la aproximación$\gamma \approx 1 + \frac{v^2}{2}$, nuestro resultado es aproximadamente

$$\frac{1}{2}Ev^2$$

descuidando términos de orden$v^4$ y superiores. La interpretación es que al$O$ reducir su energía para hacer los rayos de luz, redujo su masa de$m_o$ a$m_o - m$, donde$m = E$.$E$ Insertando el factor necesario de$c^2$ para que esto sea válido en unidades donde$c \neq 1$, tenemos el famoso

$$E = mc^2$$

Esta derivación implicó tanto una aproximación como algunos supuestos ocultos. Estos temas se exploran más a fondo en la sección 4.4. El resultado resulta ser válido para cualquier cuerpo aislado.

Encontramos que la masa no es simplemente una propiedad incorporada de las partículas que componen un objeto, siendo la masa del objeto la suma de las masas de sus partículas. Más bien, la masa y la energía son equivalentes, de manera que si el experimento de la figura a se lleva a cabo con un equilibrio suficientemente preciso, la lectura caerá por el equivalente de masa de la energía emitida como luz.

La ecuación nos$E = mc^2$ dice cuánta energía equivale a cuánta masa: el factor de conversión es el cuadrado de la velocidad de la luz,$c$. Desde$c$ un número grande, obtienes un número realmente realmente grande cuando lo multiplicas por sí mismo para obtener$c^2$. Esto significa que incluso una pequeña cantidad de masa equivale a una cantidad muy grande de energía. Por el contrario, una cantidad ordinaria de energía corresponde a una masa extremadamente pequeña, y es por ello que nadie detectó el resultado no nulo de experimentos como el de la figura hace$\PageIndex{1}$ cientos de años.

El gran evento aquí es la equivalencia masa-energía, pero también podemos cosechar un resultado para la energía de una partícula material que se mueve a cierta velocidad. Tenemos$m(γ - 1)$ por la diferencia entre$O$ la energía en marco$B$ y su energía cuando está en reposo, es decir, su energía cinética. Pero como la masa y la energía son equivalentes, asignamos$O$ una energía m cuando está en reposo. El resultado es que la energía es

$$E = m\gamma$$

(o$mγc^2$ en unidades con$c \neq 1$).

Ejemplo$\PageIndex{1}$: Electron-positron annihilation

La radiactividad natural en la tierra produce positrones, que son como electrones pero tienen la carga opuesta. Una forma de antimateria, los positrones aniquilan con electrones para producir rayos gamma, una forma de luz de alta frecuencia. Tal proceso habría sido considerado imposible antes de Einstein, porque se creía que la conservación de la masa y la energía eran principios separados, y este proceso elimina$100\%$ de la masa original. La cantidad de energía producida por la aniquilación$1\: kg$ de materia con$1\: kg$ de antimateria es

$$\begin{align*} E&= mc^2\\ &= (2\: kg)\left ( 3.0 \times 10^8 m/s^2\right )^2 \\ &= 2 \times 10^{17}\: J \end{align*}$$

¡que está en el mismo orden de magnitud que el consumo de energía de un día para toda la población mundial!

La aniquilación de positrones constituye la base de la técnica de imagen médica denominada exploración PET (tomografía por emisión de positrones), en la que se inyecta al paciente un químico emisor de positrones y se mapea mediante la emisión de rayos gamma de las partes del cuerpo donde se acumula.

Figura$\PageIndex{2}$: Arriba: Un escáner PET. Medio: Cada positrón aniquila con un electrón, produciendo dos rayos gamma que fluyen espalda con espalda. Cuando se observan simultáneamente dos rayos gamma en el anillo de detectores, se supone que provienen del mismo evento de aniquilación, y el punto en el que fueron emitidos debe estar en la línea que conecta los dos detectores. Abajo: Una exploración del torso de una persona. El cuerpo ha concentrado el trazador radiactivo alrededor del estómago, lo que indica una condición médica anormal.

Ejemplo$\PageIndex{2}$: A rusting nail

Un clavo de hierro se deja en una taza de agua hasta que se vuelve completamente oxidado. La energía liberada está a punto$0.5\: MJ$. En teoría, ¿una escala suficientemente precisa registraría un cambio en la masa? Si es así, ¿cuánto?

Solución

La energía aparecerá como calor, que se perderá para el medio ambiente. La masa-energía total de la taza, el agua y el hierro de hecho se verá disminuida por$0.5\: MJ$. (Si hubiera estado perfectamente aislado, no habría habido ningún cambio, ya que la energía térmica habría quedado atrapada en la copa). La velocidad de la luz es$c = 3×10^8\: m/s$, por lo que la conversión a unidades de masa, tenemos

$$\begin{align*} m&= \frac{E}{c^2}\\ &= \frac{0.5 \times 10^6\: J}{(3 \times 10^8\: m/s)^2}\\ &= 6 \times 10^{-12}\: kg \end{align*}$$

El cambio de masa es demasiado pequeño para medirlo con cualquier técnica práctica. Esto se debe a que el cuadrado de la velocidad de la luz es un número tan grande.

Ejemplo$\PageIndex{3}$: Relativistic kinetic energy

Hacia 1930, los aceleradores de partículas habían progresado hasta el punto en que se tomaban en cuenta rutinariamente los efectos relativistas. En 1964, W. Bertozzi realizó un experimento de propósito especial para probar las predicciones de la relatividad usando un acelerador de electrones. Los resultados se discutieron con menor detalle en el Ejemplo 3.3.1, momento en el que aún no se había visto la ecuación relativista para la energía cinética. Los electrones se aceleraron a través de una diferencia de potencial eléctrico estático$V$ a una variedad de energías cinéticas$K = eV$, y sus velocidades se inferían midiendo su tiempo de vuelo a través de una línea de haz de longitud$l = 8.4\: m$. Los pulsos eléctricos se registraron en un osciloscopio al principio y al final del tiempo de vuelo$t$. Las energías fueron confirmadas por calorimetría. La figura$\PageIndex{3}$ muestra una fotografía de muestra de una traza de osciloscopio en$V = 1.5\: MeV$.

Figura$\PageIndex{3}$: Cada división horizontal es de 9.8 ns.

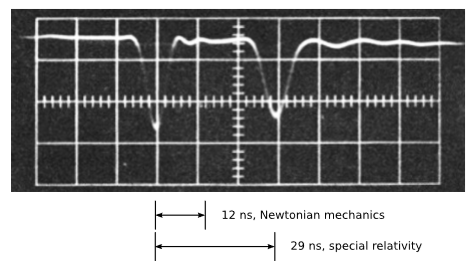
La predicción de la física newtoniana es la siguiente.

$$eV = \frac{1}{2}mv^2$$

$$\frac{v}{c} = 2.4$$

$$t = 12\: ns$$

Según la relatividad especial, tenemos:

$$eV = m(\gamma -1)c^2$$

$$\frac{v}{c} = \sqrt{1 - \left ( 1 + \frac{eV}{mc^2} \right )^{-2}} = 0.97$$

$$t = 29\: ns$$

Los resultados contradicen la predicción newtoniana y son consistentes con la relatividad especial. Según Newton, esta cantidad de energía debería haber acelerado los electrones a varias veces la velocidad de la luz. En realidad, vemos una clara demostración de la naturaleza de$c$ como una velocidad limitante.

Ejemplo$\PageIndex{4}$: Gravity bending light

Figura$\PageIndex{4}$: Luz de flexión por gravedad.

La gravedad es una atracción universal entre las cosas que tienen masa, y dado que la energía en un haz de luz equivale a una cantidad muy pequeña de masa, la luz debería verse afectada por la gravedad, aunque el efecto debería ser muy pequeño. La primera confirmación experimental de la relatividad se produjo en 1919 cuando se observó que las estrellas junto al sol durante un eclipse solar se habían desplazado un poco de su posición ordinaria. (Si no hubiera eclipse, el resplandor del sol evitaría que se observaran las estrellas). La luz de las estrellas había sido deslumbrada por la gravedad del sol. La figura$\PageIndex{4}$ es un negativo fotográfico, por lo que el círculo que parece brillante es en realidad la cara oscura de la luna, y la zona oscura es realmente la corona brillante del sol. Las estrellas, marcadas por líneas arriba y abajo entonces, aparecieron en posiciones ligeramente distintas a las normales.

Hay que tener en cuenta que estos argumentos son muy rudos y cualitativos, y no es posible producir una teoría relativista de la gravedad simplemente tomándola$E = mc^2$ y combinándola con la ley de la gravedad de Newton. Después de todo, esta ley no se refiere en absoluto al tiempo: predice que las fuerzas gravitacionales se propagan instantáneamente. Sabemos que esto no puede ser consistente con la relatividad, que prohíbe que la causa y el efecto se propaguen a cualquier velocidad mayor que$c$. Para producir una teoría relativista de la gravedad, necesitamos la relatividad general.

Razonamiento similar sugiere que puede haber estrellas —agujeros negros— tan densas que su gravedad puede impedir que la luz salga. Tales estrellas han sido detectadas, y sus propiedades parecen hasta ahora ser descritas correctamente por la relatividad general.