4.4: Sistemas con estructura interna

Objetivos de aprendizaje

• Para determinar si la prueba original de Einstein\(E = mc^2\) tiene efectos lógicos
• Determinar también si el resultado reclamado solo es válido bajo ciertas condiciones

La sección 4.2 presentó esencialmente la prueba original de Einstein\(E = mc^2\), que ha sido criticada por varios motivos. Una discusión detallada es dada por Ohanian. ¹ Dejando a un lado cuestiones que son puramente históricas o que se refieren únicamente a la prioridad académica, nos gustaría saber si la prueba tiene influencias lógicas, y también si el resultado reclamado sólo es válido bajo ciertas condiciones. Debemos considerar las siguientes preguntas:

1. ¿Importa si el sistema que se está describiendo tiene extensión espacial finita, o si el sistema está aislado?
2. ¿Importa si partes del sistema se mueven a velocidades relativistas?
3. ¿La aproximación a baja velocidad utilizada en la prueba de Einstein hace la diferencia?
4. ¿Cómo manejamos un sistema que no está hecho de partículas puntuales, por ejemplo, un condensador, en el que parte del impulso energético se encuentra en un campo eléctrico?

En el siguiente ejemplo se muestran las cuestiones 1-3 y sus conexiones lógicas; la cuestión de definición 4 se aborda en el capítulo 9.

Figura\(\PageIndex{1}\): Las líneas mundiales de dos cuentas rebotando de un lado a otro sobre un alambre.

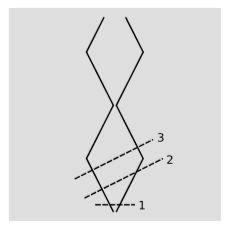
Supongamos que dos cuentas se deslizan libremente sobre un alambre, rebotando elásticamente una de la otra y también rebotando elásticamente desde los extremos del cable. Sus líneas de mundo se muestran en la figura\(\PageIndex{1}\). Digamos que cada una de las cuentas tiene masa unitaria. En marco\(o\), las cuentas se liberan del centro del alambre con velocidades\(±u\). Para concretar, pongámonos\(u = 1/2\), para que el sistema tenga movimiento interno a velocidades relativistas. En este marco, el vector energía-impulso total del sistema, en la superficie de simultaneidad etiquetada\(1\) en figura\(\PageIndex{1}\), es\(p = (2.31,0)\). Es decir, tiene una masa-energía total de\(2.31\) unidades, y un impulso total de cero (lo que significa que este es el marco del centro de masa). A medida que pasa el tiempo, un observador en este cuadro dirá que las bolas llegan a los extremos del alambre simultáneamente, momento en el que rebotan, manteniendo el mismo vector energía-impulso total\(p\). La masa del sistema es, por definición,

\[m = \sqrt{p_{t}^{2} - p_{x}^{2}} = \sqrt{2.31}\]

y esta masa se mantiene constante a medida que las bolas rebotan de un lado a otro. Ahora vamos a transformarnos en un marco\(o'\), moviéndonos a una velocidad\(v = 1/2\) relativa a\(o\). Si las velocidades se agregan linealmente en la relatividad, entonces las velocidades iniciales de las cuentas en este marco serían\(0\) y\(-1\), pero por supuesto un objeto material no puede moverse con la velocidad\(|v| = c = 1\), y las velocidades no se suman linealmente. Aplicando la fórmula correcta de adición de velocidad para la relatividad, encontramos que las cuentas tienen velocidades iniciales\(0\) y\(-0.8\) en este marco, y si calculamos su vector energía-impulso total, en superficie de simultaneidad\(2\) en figura\(\PageIndex{1}\), obtenemos\(p' = (2.67,-1.33)\). Esto es exactamente lo que habríamos conseguido tomando el vector original\(p\) y empujándolo a través de una transformación de Lorentz. Es decir, el vector energía-impulso parece estar actuando como un buen vector de cuatro, a pesar de que el sistema tiene una extensión espacial finita y contiene partes que se mueven a velocidades relativistas. En particular, esto implica que el sistema tiene la misma masa\(m = \sqrt{2.31}\) que en\(o\), ya que\(m\) es la norma del\(p\) vector, y la norma de un vector permanece igual bajo una transformación de Lorentz.

Pero ahora consideremos la superficie\(3\), que, como\(2\), observador\(o'\) considera que es una superficie de simultaneidad. En este momento,\(o'\) dice que ambas cuentas se están moviendo hacia la izquierda. Entre tiempo\(2\) y tiempo\(3\),\(o'\) dice que el impulso total del sistema ha cambiado, mientras que su masenergia total se mantuvo constante. Su masa es diferente, y el vector energía-impulso total en el\(p'\) momento no\(3\) está relacionado por una transformación de Lorentz con el valor de en ningún\(p\) momento en marco\(o\). El motivo de este mal comportamiento es que la cuenta derecha ha rebotado en el extremo derecho del cable, pero porque\(o\) y\(o'\) tienen diferentes opiniones sobre la simultaneidad,\(o'\) dice que aún no ha habido ninguna colisión coincidente para la cuenta de la izquierda.

Pero todas estas dificultades surgen sólo porque hemos dejado algo fuera. Cuando la cuenta derecha rebota en el extremo derecho del cable, esto es una colisión entre la perla y el cable. Después de la colisión, el cable rebota hacia la derecha (o se crea una vibración en él). Al ignorar el rebote del alambre, hemos violado la ley de conservación del impulso. Si tomamos en cuenta el impulso impartido al alambre, entonces el vector energía-impulso de todo el sistema se conserva, y por lo tanto debe ser el mismo en\(2\) y\(3\).

El resultado de todo esto es que\(E = mc^2\) y la naturaleza de cuatro vectores de ambos\(p\) son válidos para sistemas con extensión espacial finita, siempre que los sistemas estén aislados. “Aislado” significa simplemente que no debemos ignorar gratuitamente nada como el cable en este ejemplo que intercambia energía-impulso con nuestro sistema. Para dar una prueba general de ello, será útil desarrollar la idea del tensor estres-energía (sección 9.2), lo que permite una declaración sucinta de lo que entendemos por conservación de energía-impulso. Se da una prueba en la sección 9.3.

Referencias

¹ “\(E = mc^2\)Los errores de Einstein”, arxiv.org/abs/0805.1400