9.3: Teorema de Gauss

Objetivos de aprendizaje

• Explicar la forma simple y general del teorema de Gauss

Leyes de Conservación Integral

Hemos expresado la conservación de la carga y el impulso energético en términos de cero divergencias,

\[\frac{\partial J^a}{\partial x^a} = 0\]

\[\frac{\partial T^{ab}}{\partial x^a} = 0\]

Éstas se expresan en términos de derivados. La derivada de una función en cierto punto sólo depende del comportamiento de la función cerca de ese punto, por lo que estas son declaraciones locales de conservación. Las leyes de conservación también pueden ser declaradas globalmente: la cantidad total de algo permanece constante. Tomando a cargo como ejemplo, el observador\(o\) define las coordenadas de Minkowski\((t, x, y, z)\), y en un momento t1 dice que la cantidad total de carga en alguna región es

\[q(t_1) = \int_{t_1}J^a dS_a\]

donde el subíndice\(t_1\) significa que el integrando se va a evaluar sobre la superficie de simultaneidad\(t = t_1\), y\(dS_a = (dx dy dz, 0, 0, 0)\) es un elemento de\(3\) -volumen expresado como un covector. El cargo en algún momento posterior\(t_2\) estaría dado por una integral similar. Si se conserva la carga, y si nuestra región está rodeada por una región vacía a través de la cual no entra ni sale ningún cargo, entonces deberíamos haberlo hecho\(q(t_2) = q(t_1)\).

Una forma simple del teorema de Gauss

La conexión entre las leyes de conservación locales y globales es proporcionada por un teorema llamado teorema de Gauss. En tu curso sobre electromagnetismo aprendiste la ley de Gauss, que relaciona el flujo eléctrico a través de una superficie cerrada con la carga contenida dentro de la superficie. En el caso donde no hay cargos, dice que el flujo a través de dicha superficie se cancela.

Figura\(\PageIndex{1}\): Entran tres líneas y salen tres. Estas podrían ser líneas de campo o líneas mundiales.

La interpretación es que dado que las líneas de campo solo comienzan o terminan en cargas, la ausencia de cualquier carga significa que las líneas no pueden comenzar o terminar, y por lo tanto, como en la figura\(\PageIndex{1}\), cualquier línea de campo que entre en la superficie (aportando algún flujo negativo) eventualmente debe volver a salir (creando algunos positivos flujo que cancela el negativo). Pero no hay nada de figura\(\PageIndex{1}\) que requiera que se interprete como un dibujo de líneas de campo eléctrico. Con la misma facilidad podría ser un dibujo de las líneas del mundo de algunas partículas cargadas en\(1 + 1\) dimensiones. La parte inferior del rectángulo sería entonces la superficie en\(t_1\) y la parte superior\(t_2\). Nosotros tenemos\(q(t_1) = 3\) y\(q(t_2) = 3\) también.

Por simplicidad, comencemos con una versión muy restringida del teorema de Gauss. Deje que un campo vectorial\(J^a\) se defina en dos dimensiones. (No nos importa si las dos dimensiones son espaciosas o una espacial y otra temporal; es decir, el teorema de Gauss no depende de la firma de la métrica). Dejar\(R\) ser un área rectangular, y dejar\(S\) ser su límite. Definir el flujo del campo a través\(S\) de

\[\Phi = \int_{S}J^a dS_a\]

donde la integral se va a tomar sobre los cuatro lados, y el covector\(dS_a\) apunta hacia afuera. Si el campo tiene divergencia cero\(\frac{\partial J^a}{\partial x^a} = 0\), entonces el flujo es cero.

Prueba: Definir coordenadas\(x\) y\(y\) alineadas con el rectángulo. A lo largo de la parte superior del rectángulo, el elemento de la superficie, orientado hacia afuera, es\(dS = (0, dx)\), por lo que la contribución al flujo desde la parte superior es

\[\Phi _{top} = \int_{top}J^y (y_{top}) dx\]

En la parte inferior, una orientación hacia afuera da\(dS = (0, -dx)\), por lo

\[\Phi _{bottom} = \int_{bottom}J^y (y_{bottom}) dx\]

Utilizando el teorema fundamental del cálculo, la suma de estos es

\[\Phi _{top} + \Phi _{bottom} = \int_{R}\frac{\partial J^y}{\partial y}dy dx\]

Añadiendo en las expresiones similares para la izquierda y la derecha, obtenemos

\[\Phi = \int_{R}\left (\frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} \right )dy dx\]

Pero el integrando es la divergencia, que es cero por suposición, así\(Φ = 0\) como se afirma.

La forma general del teorema de Gauss

Si bien las coordenadas fueron etiquetadas\(x\) y\(y\), la prueba no hizo uso de la métrica, por lo que el resultado es igualmente válido independientemente de la firma. El rectángulo podría haber sido igualmente un rectángulo en\(1 + 1\) espacio-tiempo dimensional. La generalización a\(n\) las dimensiones también es automática, y todo también se lleva a cabo sin modificaciones si reemplazamos el vector\(J^a\) con un tensor como el\(T^{ab}\) que tiene más índices — el índice extra\(b\) solo viene a lo largo para el paseo. A veces, como con la ley de Gauss en el electromagnetismo, nos interesan los campos cuyas divergencias no son cero. El teorema de Gauss se convierte entonces

\[\int_{S} J^a dS_a= \int_{R}\frac{\partial J^a}{\partial x^a} dv\]

donde\(dv\) está el elemento de\(n\) -volumen. En\(3 + 1\) dimensiones podríamos usar coordenadas Minkowski para escribir el elemento de\(4\) -volumen como\(dv = dt dx dy dz\), y aunque esta expresión esté escrita en términos de estas coordenadas específicas, en realidad es Lorentz invariante (sección 2.5).

Figura\(\PageIndex{2}\): Prueba del teorema de Gauss para una región con forma arbitraria.

La generalización a una región\(R\) con una forma arbitraria, figura\(\PageIndex{2}\), es menos trivial. La idea básica es descomponer la región en cajas rectangulares, figura\(\PageIndex{2}\) (1). Donde las caras de dos cajas coinciden en el interior de\(R\), sus propias direcciones exteriores son opuestas. Por lo tanto, si sumamos los fundentes a través de las superficies de todas las cajas, las aportaciones en el interior se cancelan, y nos quedamos solo con las aportaciones exteriores. Si\(R\) pudiera ser diseccionado exactamente en cajas, entonces esto completaría la prueba, ya que la suma de las contribuciones exteriores sería la misma que la del flujo a través\(S\), y el lado izquierdo del teorema de Gauss sería aditiva sobre las cajas, como lo es el lado derecho.

La dificultad surge porque una forma suave normalmente no se puede construir a partir de ladrillos, hecho que es bien conocido por los entusiastas de Lego que construyen elaborados modelos de la Estrella de la Muerte. Podríamos argumentar sobre bases físicas que ninguna medición del flujo en el mundo real puede depender de la estructura granular de\(S\) a escalas arbitrariamente pequeñas, pero esto se siente un poco insatisfactorio. A modo de comparación, no es estrictamente cierto que las áreas superficiales puedan tratarse de esta manera. Por ejemplo, si aproximamos una unidad\(3\) -esfera usando cajas cada vez más pequeñas, el límite de la superficie es\(6π\), que es bastante mayor que la superficie\(4π/3\) de la superficie limitante.

En cambio, consideramos explícitamente las piezas no rectangulares en la superficie, como la de la figura\(\PageIndex{2}\) (2). En este dibujo en\(n = 2\) dimensiones, la parte superior de esta pieza es aproximadamente una línea, y en el límite vamos a estar considerando, donde su ancho se convierte en un infinitesimalmente pequeño\(dx\), el error incurrido al aproximarla como línea será insignificante. Definimos vectores\(dx\) y\(dx ∗\) como se muestra en la figura. En más de las dos dimensiones mostradas en la figura, aproximaríamos la superficie superior como un paralelepípedo\((n - 1)\) -dimensional abarcado por vectores\(dx ∗ , dy ∗ , . . .\) Este es el punto en el que el uso del covector\(S_a\) vale la pena al simplificar enormemente la prueba. ¹ Aplicando esto a la parte superior del triángulo,\(dS\) se define como la función lineal que toma un vector\(J\) y da el\(n\) -volumen abarcado por\(J\) junto con\(dx ∗ , . . .\)

Llame a la coordenada vertical en el diagrama\(t\), y considere la contribución al flujo desde el componente\(J\) de tiempo,\(J^t\). Debido a que el tamaño del triángulo es un infinitesimal de orden\(dx\), podemos aproximarnos\(J^t\) como una constante a lo largo del triángulo, mientras incurre únicamente en un error de orden\(dx\). (Al afirmar el teorema de Gauss en términos de derivados de\(J\), asumimos implícitamente que era diferenciable, por lo que no es posible que salte discontinuamente). Dado que\(dS\) depende linealmente no solo de\(J\) sino de todos los vectores, la diferencia entre el flujo en la parte superior e inferior del triángulo es proporcional al área abarcada por\(J\) y\(dx ∗ - dx\). Pero este último vector está en la\(t\) dirección, y por lo tanto el área que abarca cuando se toma con\(J^t\) es aproximadamente cero. Por lo tanto, la\(J^t\) contribución del flujo a través del triángulo es cero. Para estimar el posible error debido a las aproximaciones, tenemos que contar potencias de\(dx\). La posible variación de\(J^t\) sobre el triángulo es de orden\((dx)^1\). El covector\(dS\) es de orden\((dx)^{n-1}\), por lo que el posible error en el flujo es de orden\((dx)^n\).

Esto fue sólo una estimación de una parte del flujo, la parte aportada por el componente\(J^t\). No obstante, obtenemos la misma estimación para las otras partes. Por ejemplo, si nos referimos a las dos dimensiones en la figura\(\PageIndex{1}\) (2) como\(t\) y\(x\), entonces intercambiar los roles de\(t\) y\(x\) en el argumento anterior produce la misma estimación de error para la contribución de\(J^x\).

Esto es bueno. Cuando iniciamos este argumento, nos motivó ser cautelosos por nuestra observación de que una cantidad como el área superficial de no se\(R\) puede calcular como el límite de la superficie aproximada usando cajas. La razón por la que tenemos ese problema para la superficie es que el error en la aproximación en un parche pequeño es de orden\((dx)^{n-1}\), lo que es un infinitesimal del mismo orden que la superficie del parche mismo. Por lo tanto, cuando reducimos las cajas, el error no se vuelve pequeño en comparación con el área total. Pero cuando consideramos el flujo, el error contibutado por cada una de las piezas de forma irregular cerca de la superficie va como\((dx)^n\), que es del orden del\(n\) -volumen de la pieza. Este volumen va a cero en el límite donde las cajas se hacen pequeñas, y por lo tanto el error va a cero también. Esto establece la generalización del teorema de Gauss a una región\(R\) de forma arbitraria.

9.3.4 El vector energía-impulso

El célebre de Einstein\(E = mc^2\) es un caso especial de la afirmación de que el impulso energético se conserva, se transforma como un cuatro vectores y tiene una norma\(m\) igual a la masa de descanso. La Sección 4.4 exploró algunos de los problemas con el intento original de Einstein de probar esta afirmación, pero solo ahora estamos preparados para resolverlos por completo. Uno de los problemas fue el definitivo de lo que queremos decir con el impulso energético de un sistema que no está compuesto por partículas puntuales. La respuesta es que para cualquier fenómeno que lleve impulso energético, debemos decidir cómo contribuye al tensor estres-energía. Por ejemplo, el tensor tensión-energía de los campos eléctrico y magnético se describe en la sección 10.6.

Figura\(\PageIndex{3}\): Conservación del vector energía-impulso integrado.

Por las razones discutidas en la Sección 4.4, es necesario suponer que el impulso energético se conserva localmente, y también que el sistema que se describe está aislado. La conservación local se describe por la propiedad de divergencia cero del tensor de tensión-energía,\(\frac{\partial T^{ab}}{\partial x^a} = 0\). Una vez que asumimos la conservación local, la figura\(\PageIndex{3}\) muestra cómo probar la conservación del vector energía-impulso integrado utilizando el teorema de Gauss. Fijar un marco de referencia\(o\). Rodeando el sistema, mostrado como una corriente oscura que fluye a través del espacio-tiempo, dibujamos una caja. La caja está delimitada en su lado pasado por una superficie que\(o\) considera una superficie de simultaneidad\(s_A\), e igualmente en el lado futuro\(s_B\). En realidad no importa si los lados de la caja son rectos o curvos según o. Lo que sí importa es que debido a que el sistema está aislado, tenemos suficiente espacio para que entre el sistema y los lados de la caja pueda haber una región de vacío, en la que el tensor de energía de estrés desaparece. Observador\(o\) dice que en el momento inicial correspondiente a\(s_A\), la cantidad total de energía-impulso en el sistema fue

\[p_{A}^{\mu } = -\int_{s_A} T^{\mu \nu } dS_{\nu }\]

donde ocurre el signo menos porque tomamos para apuntar\(dS_{\nu }\) hacia afuera, por compatibilidad con el teorema de Gauss, y esto lo hace antiparalelo al vector de velocidad\(o\), que es lo opuesto a la orientación definida en las ecuaciones 9.2.1 y 9.2.2. En el momento final tenemos

\[p_{B}^{\mu } = \int_{s_B} T^{\mu \nu } dS_{\nu }\]

con un signo más porque la dirección hacia afuera es ahora la misma que la dirección de\(o\). Debido a la región de vacío, no hay flujo a través de los lados de la caja, y por lo tanto por el teorema de Gauss

\[p_{B}^{\mu } - p_{A}^{\mu } = 0\]

El vector energía-impulso se ha conservado globalmente según\(o\).

Figura\(\PageIndex{4}\): Transformación de Lorentz del vector energía-momento integrado.

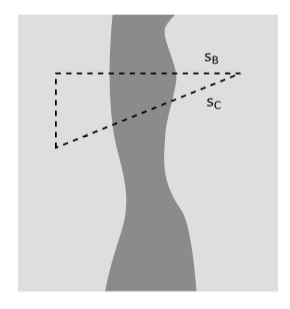
También necesitamos demostrar que el impulso energético integrado se transforma correctamente como un cuatro vector. Para demostrarlo, aplicamos el teorema de Gauss a la región mostrada en la figura\(\PageIndex{4}\), donde\(s_C\) es una superficie de simultaneidad según algún otro observador\(o'\). El teorema de Gauss nos dice eso\(p_B = p_C\), lo que significa que el impulso energético en las dos superficies es el mismo vector en el sentido absoluto —pero esto no significa que los dos vectores tengan los mismos componentes medidos por diferentes observadores. Observador\(o\) dice que\(s_B\) es una superficie de simultaneidad, y por lo tanto considera que\(p_B\) es el impulso energético total en un momento determinado. Ella dice que la masa-energía total es\(p_{B}^{\mu } o_{\mu }\) (Ecuación 9.2.1), y de manera similar para el impulso total en las tres direcciones espaciales\(s_1\),\(s_2\), y\(s_3\) (Ecuación 9.2.2). Observador\(o'\), por su parte, considera que\(s_C\) es una superficie de simultaneidad, y tiene las mismas interpretaciones para cantidades como\(p_{C}^{\mu } o'_{\mu }\). Pero esto es solo una manera de decir eso\(p_{B}^{\mu }\) y\(p_{C}^{\mu }\) están relacionados entre sí por un cambio de bases de\((o, s_1, s_2, s_3)\) a\((o', s'_1, s'_2, s'_3)\). Un cambio de base como este es justo lo que queremos decir con una transformación de Lorentz, por lo que el impulso energético integrado\(p\) se transforma como un cuatro vector.

9.3.5 Momento angular

En la sección 8.2, dimos argumentos de plausibilidad física y matemática para definir el momento angular relativista como\(L^{ab} = r^a p^b - r^b p^a\). Ahora podemos demostrar que esta cantidad está realmente conservada. Así como el flujo de energía-momento\(p^a\) es el tensor de tensión-energía\(T^{ab}\), podemos tomar el momento angular\(L^{ab}\) y definir su flujo\(λ^{abc} = r^a T^{bc} - r^b T^{ac}\). Un observador con vector de velocidad\(o^c\) dice que la densidad de energía-momento es\(T^{ac}o_c\) y la densidad del momento angular es\(λ^{abc}o_c\). Si podemos demostrar que la divergencia de\(λ\) respecto a su tercer índice es cero, entonces se deduce que se conserva el momento angular. La divergencia es

\[\frac{\partial \lambda ^{abc}}{\partial x^c} = \frac{\partial }{\partial x^c} \left (r^a T^{bc} - r^b T^{ac} \right )\]

La regla del producto da

\[\frac{\partial \lambda ^{abc}}{\partial x^c} = \delta _{c}^{a} T^{bc} + r^a \frac{\partial }{\partial x^c} T^{bc} - \delta _{c}^{b} T^{ac} - r^b \frac{\partial }{\partial x^c} T^{ac}\]

donde\(\delta _{j}^{i}\), llamado el delta de Kronecker, se define como\(1\) si\(i = j\) y\(0\) si\(i \neq j\). La divergencia del tensor tensión-energía es cero, por lo que los términos segundo y cuarto desaparecen, y

\[\begin{align*} \frac{\partial \lambda ^{abc}}{\partial x^c} &= \delta _{c}^{a} T^{bc} - \delta _{c}^{b} T^{ac}\\ &= T^{ba} - T^{ab} \end{align*}\]

pero esto es cero porque el tensor de tensión-energía es simétrico.

Referencias

¹ Aquí un ejemplo de las feas complicaciones que ocurren si uno no tiene acceso a esta pieza de tecnología. En el enfoque de baja tecnología, en el espacio euclidiano, se define un elemento de área de superficie\(dA = \hat{n} dA\), donde el vector unitario\(\hat {n}\) se dirige hacia afuera con\(\hat{n} \cdot \hat{n} = 1\). Pero en una firma como +−−−, podríamos tener una región\(R\) tal que sobre alguna gran área de la superficie limítrofe\(S\), la dirección normal fuera parecida a la luz. Por lo tanto, sería imposible escalar\(\hat {n}\) así que eso\(\hat{n} \cdot \hat{n}\) era cualquier cosa menos cero. Como ejemplo de cuánto trabajo es resolver este tipo de problemas utilizando herramientas de la edad de piedra, ver Synge, Relatividad: La teoría especial, VIII, §6-7, donde el argumento completo ocupa 22 páginas.