5.1: ¿Qué es el Movimiento Inercial?

Objetivos de aprendizaje

• Explicar el movimiento inercial

En la sección 2.3, declaré lo siguiente como axioma de relatividad especial:

P4: Existen marcos inerciales de referencia. Se trata de marcos en los que las partículas se mueven a velocidad constante si no están sujetas a ninguna fuerza. Podemos construir tal marco usando una partícula particular, que no está sujeta a ninguna fuerza, como punto de referencia. El movimiento inercial es modelado por vectores y paralelismo.

Esta es una típica reafirmación moderna de la primera ley de Newton. Afirma definir marcos inerciales y afirma que existen.

Una definición operativa

Figura\(\PageIndex{1}\): La cámara esférica, mostrada en una vista en corte, tiene capas de blindaje para excluir todas las fuerzas no gravitacionales conocidas. Los tres cañones, en ángulo recto entre sí, disparan balas. Una vez que la cámara ha sido calibrada marcando las tres trayectorias de línea discontinua en condiciones de caída libre, un observador dentro de la cámara siempre puede decir si se encuentra en un marco ninercial.

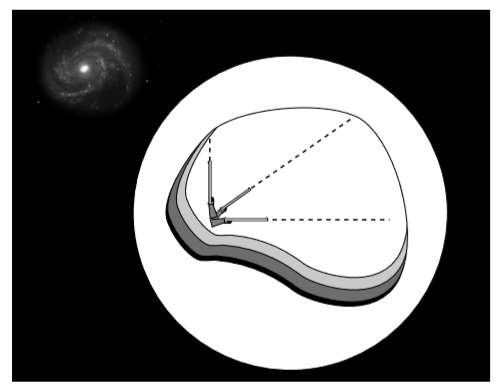
De acuerdo con la filosofía del operacionalismo, deberíamos poder traducir la definición en un método para probar si un marco dado es realmente inercial. La figura\(\PageIndex{1}\) muestra una variación idealizada de un dispositivo realmente construido para este propósito por Harold Waage en Princeton como demostración de conferencia para ser utilizado por su compañero en el crimen John Wheeler. Construimos una cámara sellada cuyo contenido está aislado lo más posible de las fuerzas externas. De las cuatro fuerzas conocidas de la naturaleza, las que sabemos excluir son la fuerza nuclear fuerte, la fuerza nuclear débil y la fuerza electromagnética. La fuerza nuclear fuerte tiene un rango de solo aproximadamente\(1\: fm\) (\(10^{-15} m\)), así que para excluirla simplemente necesitamos hacer que la cámara sea más gruesa que esa, y también rodearla con suficiente cera de parafina para mantener fuera cualquier neutrón que pase pasar volando. La débil fuerza nuclear también tiene un alcance corto, y aunque el blindaje contra neutrinos es una imposibilidad práctica, su influencia en el aparato interior será insignificante. Para protegernos contra las fuerzas electromagnéticas, rodeamos la cámara con una jaula de Faraday y una lámina sólida de mu-metal. Por último, nos aseguramos de que la cámara no esté siendo tocada por ninguna materia circundante, por lo que se excluyen las fuerzas eléctricas residuales de corto alcance (fuerzas pegajosas, enlaces químicos, etc.). Es decir, la cámara no puede ser soportada; es de caída libre.

Crucialmente, el blindaje no excluye las fuerzas gravitacionales. De hecho, no existe una forma conocida de proteger contra los efectos gravitacionales como la atracción de otras masas o la propagación de ondas gravitacionales. (Debido a que el blindaje es esférico, no ejerce ninguna fuerza gravitacional propia sobre el aparato interior.)

En su interior, una observadora realiza una calibración inicial disparando balas a lo largo de tres ejes cartesianos y trazando sus caminos, los cuales define como lineales. (También puede asegurarse de que la cámara no esté girando, por ejemplo, comprobando las fuerzas de Coriolis dependientes de la velocidad). Después de la calibración inicial, siempre puede decir si se encuentra o no en un marco inercial. Simplemente tiene que disparar las balas, y ver si siguen o no los caminos precalibrados. Por ejemplo, puede detectar que el marco se ha vuelto no inercial si la cámara es girada, se le permite descansar en el suelo, o acelerada por un motor de cohete.

Isaac Newton habría sido extremadamente infeliz con nuestra definición. “Esto es absurdo”, dice. “La forma en que la has definido, mi calle en Londres no es inercial. ” La mecánica newtoniana solo hace predicciones si ingresamos los datos correctos sobre toda la masa del universo. Dado este tipo de conocimientos, podemos dar cuenta adecuadamente de todas las fuerzas gravitacionales, y definir la calle en Londres como un marco inercial porque en ese marco, los árboles y las casas tienen cero fuerza total sobre ellos y no aceleran. Pero el espacio-tiempo no es galileo. En la descripción especial del espacio-tiempo de la relatividad, la información se propaga a una velocidad máxima de\(c\), por lo que siempre habrá partes distantes del universo que nunca podremos conocer, porque la información de esas regiones aún no ha tenido tiempo de llegar a nosotros.

Ejemplo\(\PageIndex{1}\): Rotation is noninertial

La figura\(\PageIndex{2}\) muestra un ejemplo hipotético propuesto por Einstein. Un planeta gira alrededor de su eje y por lo tanto tiene una protuberancia ecuatorial. El otro planeta no gira y no tiene ninguno. Tanto la mecánica newtoniana como la relatividad especial hacen estas predicciones, y aunque el escenario es idealizado y poco realista, no cabe duda de que sus predicciones son correctas para esta situación, porque las dos teorías han sido probadas en casos similares. Esto también concuerda con nuestra definición operativa de movimiento inercial como se indicó anteriormente. El movimiento rotacional es no inercial.

Figura\(\PageIndex{2}\): Ejemplo hipotético propuesto por Einstein

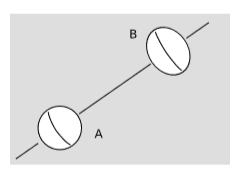
Esto molestó a Einstein por la siguiente razón. Si los habitantes de los dos planetas pueden mirar hacia arriba en el cielo a las “estrellas fijas”, tienen una explicación clara de la razón de la diferencia de forma. La gente en el planeta A no ve que las estrellas suban o se ponen, e infieren que esto se debe a que viven en un mundo no rotativo. Los habitantes del planeta B sí ven a las estrellas elevarse y ponerse, tal como lo hacen aquí en la tierra, así inferyen, tal como lo hizo Copérnico, que su planeta gira.

Pero supongamos, dijo Einstein, que los dos planetas existen solos en un universo por lo demás vacío. No hay estrellas. Entonces es igualmente válido que alguien en cualquiera de los dos planetas diga que es el que no gira. Cada planeta gira en relación con el otro planeta, pero la situación ahora parece completamente simétrica. Einstein se tomó en serio este argumento y consideró que mostraba un defecto en la relatividad especial. Esperaba que su teoría de la relatividad general solucionara este problema, y predijera que en otro universo vacío sabio, ninguno de los planetas mostraría ningún bulto de marea. En realidad, un mayor estudio de la teoría general de la relatividad mostró que hizo la misma predicción que la relatividad especial. Los teóricos han construido otras teorías de la gravedad, más prominentemente la teoría Brans-Dicke, que sí se comportan más de la manera que la intuición física de Einstein esperaba. Sin embargo, las pruebas precisas del sistema solar han apoyado la relatividad general en lugar de la gravedad Brans-Dicke, por lo que parece bien asentada ahora que el movimiento rotacional realmente no debería considerarse inercial.

Equivalencia de Masa Inercial y Gravitacional

Todo el razonamiento anterior depende de la cancelación perfecta a la que se refiere Newton: dado que las fuerzas gravitacionales son proporcionales a la masa, y la aceleración es inversamente proporcional a la masa, el resultado es que las aceleraciones causadas por la gravedad son independientes de la masa. Esta es la universalidad de la caída libre, que fue famosa por Galileo, Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Según la alumna de Galileo, Viviani, Galileo arrojó una bala de cañón y una bola de mosquete simultáneamente desde la torre inclinada de Pisa, y observó que chocaron contra el suelo casi al mismo tiempo. Esto contradice la idea largamente aceptada por Aristóteles de que los objetos más pesados cayeron más rápido

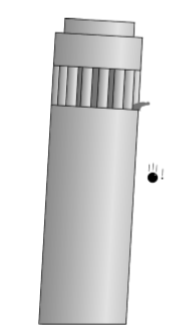
Supongamos que, por el contrario, tuvimos acceso a alguna materia que era inmune a la gravedad. Se vende bajo la marca FloatyStuff ^TM. La cancelación falla ahora. Digamos que los gánsteres alienígenas aterrizan en un platillo volador, te secuestran de tu patio trasero, te golpean en la cabeza y te llevan lejos. Cuando recuperas la conciencia, estás encerrado en una cabina sellada en su nave espacial. Sacas tu llavero de tu bolsillo y lo sueltas, y observas que acelera hacia el suelo con una aceleración que parece bastante más lenta de lo que estás acostumbrado en la tierra, quizás un tercio de un gee. Hay dos posibles explicaciones para ello. Una es que los extraterrestres te han llevado a algún otro planeta, tal vez Marte, donde la fuerza de la gravedad es un tercio de lo que tenemos en la tierra. La otra es que tu llavero realmente no aceleró en absoluto: todavía estás dentro del platillo volador, que está acelerando a un tercio de un gee, así que realmente fue la baraja la que aceleró y golpeó las teclas.

No hay absolutamente ninguna manera de saber cuál de estos dos escenarios es realmente el caso, a menos que tenga un pedazo de FloatyStuff en su otro bolsillo. Si sueltas el FloatyStuff y se cierne sobre la cubierta, entonces estás en otro planeta y experimentas una gravedad genuina; tu llavero respondió a la gravedad, pero el FloatyStuff no lo hizo.Pero si sueltas el FloatyStuff y lo ves golpear la cubierta, entonces el platillo volador está acelerando a través del espacio exterior.