5.2: El principio de equivalencia

Objetivos de aprendizaje

• Explicar el principio de equivalencia

Equivalencia de aceleración a un campo gravitacional

La inexistencia de FloatyStuff en nuestro universo es un caso especial del principio de equivalencia. El principio de equivalencia establece que una aceleración (como la aceleración del platillo volador) siempre es equivalente a un campo gravitacional, y ninguna observación puede jamás notar la diferencia sin hacer referencia a algo externo. (Y supongamos que tiene algún punto de referencia externo — ¿cómo sabría si se estaba acelerando?)

Experimentos de Eötvös

FloatyStuff sería un ejemplo extremo, pero si hubiera alguna violación a la universalidad de la caída libre, por pequeña que fuera, entonces se falsificaría el principio de equivalencia. Desde la época de Galileo, los métodos experimentales han tenido varios siglos en los que mejorar, y la segunda ley ha sido sometida a pruebas similares con una precisión exponencialmente mejorada. Para tal experimento en 1993, ¹ físicos en la Universidad de Pisa (!) construyó un disco de metal con semicírculos de cobre y tungsteno unidos en sus bordes de flat. Evacuaron el aire de un eje vertical y dejaron caer el disco por él\(142\) veces, utilizando láseres para medir cualquier rotación minúscula que resultaría si las aceleraciones del cobre y el tungsteno fueran muy ligeramente diferentes. Los resultados fueron estadísticamente consistentes con la rotación cero, y pusieron un límite superior de\(1×10^{-9}\) sobre la diferencia fraccionaria en la aceleración

\[\frac{ |g_{copper} - g_{tungsten}|}{g}\]

Los experimentos de este tipo se llaman experimentos de Eötvös, después de Loránd Eötvös, quien realizó las primeras versiones modernas y de alta precisión.

Figura\(\PageIndex{1}\): Loránd Eötvös (1848-1919).

Ejemplo\(\PageIndex{1}\): The artificial horizon

Figura\(\PageIndex{2}\): Un horizonte artificial.

El piloto de un avión no siempre puede decir fácilmente qué camino está arriba. El horizonte puede no estar nivelado simplemente porque el suelo tiene una pendiente real, y en cualquier caso el horizonte puede no ser visible si el clima es brumoso. Uno podría imaginar que el problema podría resolverse simplemente colgando un péndulo y observando en qué dirección apuntaba, pero por el principio de equivalencia el péndulo no puede distinguir entre un campo gravitacional y una aceleración de la aeronave en relación con el suelo —ni ningún otro acelerómetro, como el oído interno del piloto. Por ejemplo, cuando el avión gira hacia la derecha, los acelerómetros serán engañados para que crean que “abajo” está abajo y hacia la izquierda. Para sortear este problema, los aviones utilizan un dispositivo llamado horizonte artificial, que es esencialmente un giroscopio. El giroscopio tiene que ser inicializado cuando se sabe que el plano está orientado en un plano horizontal. Ningún giroscopio es perfecto, por lo que con el tiempo va a la deriva. Por esta razón el instrumento también contiene un acelerómetro, y el giroscopio se restablece automáticamente a acuerdo con el acelerómetro, con una constante de tiempo de varios minutos. Si el avión está florecido en círculos durante varios minutos, el horizonte artificial será engañado para indicar que la dirección equivocada es vertical.

Gravedad sin gravedad

Vivimos inmersos en el campo gravitacional de la tierra, y ahí es donde hacemos casi todos nuestros experimentos de física. Es sorprendente, entonces, que la relatividad especial pueda confirmarse en experimentos terrestres, a veces con una precisión fenomónica, como en la prueba de\(10\) figura significativa del experimento Ives-Stilwell de la ecuación de cambio Doppler relativista. ¿Cómo puede ser esto, ya que se supone que la relatividad especial es la versión de la relatividad que no puede manejar la gravedad? El principio de equivalencia proporciona una respuesta. Si el único efecto gravitacional en tu experimento es un campo uniforme\(g\), entonces es válido que describas tu experimento como hecho en una región sin gravedad alguna, pero en un laboratorio cuyo floor pasó a haber ido acelerando hacia arriba con una aceleración\(-g\). La relatividad especial funciona bien en tales situaciones, porque cambiar a un marco de referencia acelerado no tiene ningún efecto sobre la flotabilidad del espacio-tiempo. Tenga en cuenta que la sonda de gravedad B orbitó la tierra, por lo que el campo que experimentó varió en dirección, provocando que el argumento anterior fallara; los efectos que observó no fueron explicables por relatividad especial.

Desplazamientos Doppler gravitacionales

Figura\(\PageIndex{3}\): 1. Una onda de luz se emite hacia arriba desde el piso del elevador. El elevador acelera hacia arriba. 2. Para cuando se detecta la onda de luz en el techo, el elevador ha cambiado su velocidad, por lo que la onda se detecta con un desplazamiento Doppler.

Para un ejemplo de un experimento específicamente gravitacional que es explicable por relatividad especial, y que realmente se ha llevado a cabo, En un laboratorio acelerando hacia arriba, una onda de luz emitida desde el suelo sería desplazada por Doppler hacia frecuencias más bajas cuando se observaba en el techo, debido al cambio en la velocidad del receptor durante el tiempo de vuelo de la onda. El efecto viene dado por

\[\frac{\Delta f}{f} \approx \frac{-a\Delta x}{c^2}\]

donde a es la aceleración del laboratorio,\(∆x\) es la altura del piso al techo, y\(c\) es la velocidad de la luz.

En unidades con\(c = 1\), tenemos

\[\frac{\Delta f}{f} \approx -a\Delta x\]

Por el principio de equivalencia, encontramos que cuando tal experimento se realiza en un campo gravitacional\(g\), debe haber un efecto gravitacional sobre la frecuencia

\[\frac{\Delta f}{f} \approx -g\Delta x\]

Esto se puede expresar de manera más compacta como

\[\frac{\Delta f}{f} \approx -\Delta \Phi\]

donde\(Φ\) está el potencial gravitacional, es decir, la energía gravitacional por unidad de masa.

Figura\(\PageIndex{4}\): Libra y Rebka en la parte superior e inferior de la torre.

En 1959, Pound y Rebka ² llevaron a cabo un experimento en una torre de Harvard. Los rayos gamma de fueron emitidos por una\(^{57}\textrm{Fe}\) fuente en la parte inferior y detectados en la parte superior, habiéndose elevado\(∆x = 22.6 m\). El principio de equivalencia predice un desplazamiento fraccionario de frecuencia debido a la gravedad de\(2.46×10^{-15}\). Esto es muy pequeño, y normalmente habría sido enmascarado por los efectos de retroceso, pero al explotar el efecto Mössbauer Pound y Rebka midieron el cambio a ser\((2.56±0.25)×10^{-15}\).

Una métrica variable

En el experimento Libra-Rebka, los núcleos que emiten los rayos gamma a frecuencia\(f\) pueden considerarse como pequeños relojes. Cada cresta de onda que se propaga hacia arriba es una señal que dice que el reloj ha mareado una vez. Un observador en la parte superior de la torre encuentra que las señales llegan a la frecuencia más baja\(f'\), y concluye naturalmente que los relojes en la parte inferior se habían ralentizado debido a algún tipo de efecto de dilatación temporal derivado de la gravedad.

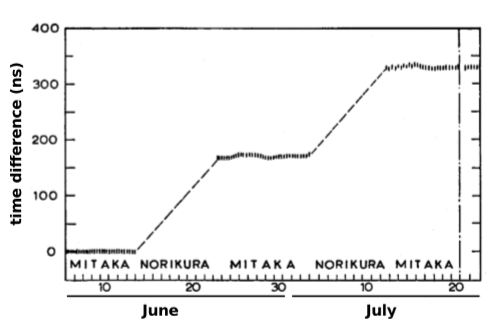
Esto puede parecer un gran salto conceptual, pero se ha confirmado usando relojes atómicos. En un experimento de 1978 de Iijima y Fujiwara, figura\(\PageIndex{5}\), relojes atómicos idénticos se mantuvieron en reposo en la parte superior e inferior de una montaña cerca de Tokio. Las discrepancias entre los relojes fueron consistentes con las predicciones del principio de equivalencia. El cambio Doppler gravitacional también fue uno de los efectos que llevaron al resultado no nulo del experimento Hafele-Keating, en el que los relojes atómicos se flotaban alrededor del mundo a bordo de aviones comerciales de pasajeros. Cada vez que usas el sistema GPS, estás haciendo uso de estos efectos.

Figura\(\PageIndex{5}\): Un gráfico que muestra la diferencia de tiempo entre dos relojes atómicos. Un reloj se mantuvo en el Observatorio Mitaka, a 58 m sobre el nivel del mar. El otro fue trasladado de ida y vuelta a un segundo observatorio, la Estación Norikura Corona, en la cima del volcán Norikura, a 2876 m sobre el nivel del mar. Las mesetas en la gráfica son datos de los periodos en los que se compararon los relojes uno al lado del otro en Mitaka. La diferencia entre una meseta y la siguiente muestra un efecto gravitacional sobre la tasa de flujo de tiempo, acumulado durante el período en que el reloj móvil estaba en la cima de Norikura.

Partiendo únicamente del supuesto aparentemente inocuo del principio de equivalencia, nos llevan a conclusiones sorprendentemente trascendentales. Encontramos que el tiempo fluye a diferentes velocidades dependiendo de la altura dentro de un campo gravitacional. Dado que la métrica puede interpretarse como una medida de la cantidad de tiempo adecuado a lo largo de una línea mundial dada, concluimos que no siempre podemos expresar la métrica en la forma familiar\(\tau ^2 = (+1)\Delta t^2 + (-1)\Delta x^2\) con coeficientes fijos\(+1\) y\(-1\). Supongamos que la\(t\) coordenada está definida por la sincronización de radio. Entonces el\(+1\) en la métrica necesita ser reemplazado por aproximadamente\(1 + 2Φ\), donde tomamos\(Φ = 0\) por convención a la altura del reloj estándar que coordina la sincronización.

Hay que tener en cuenta que aunque hemos conectado la gravedad al aparato de medición de relatividad especial, no hay curvatura del espacio-tiempo, así que lo que estamos haciendo aquí sigue siendo relatividad especial, no relatividad general. De hecho no hay nada más misterioso pasando aquí que un cambio de nombre de eventos espacio-tiempo a través de un cambio de coordenadas. El cambio de nombre podría ser conveniente si usáramos puntos de referencia basados en la tierra para medir la\(x\) coordenada. Pero si nos apetecía, podríamos cambiar a un buen marco de referencia inercial, uno que fuera de caída libre. En este marco, obtendríamos exactamente la misma predicción para los resultados de cualquier experimento. Por ejemplo, el observador de caída libre explicaría el resultado del experimento Libra-Rebka como derivado de la aceleración ascendente del detector alejándose de la fuente.

Referencias

¹ Carusotto et al., “Límites a la violación de la universalidad g con un experimento de Galileotipo”, Phys Let A183 (1993) 355. Disponible gratuitamente en línea en researchgate.net.

² Phys. Rev. Let. 4 (1960) 337