6.3: El covector frecuencia-número de ondas

Objetivos de aprendizaje

• Estudiar\(\omega \to \) el covector frecuencia-longitud de onda

Generalizando de\(0 + 1\) dimensiones a\(3 + 1\), podríamos tener un observador moviéndose inercialmente a lo largo del vector de velocidad\(\to o\), mientras cuenta la fase\(φ\) (en radianes) de una onda plana (tal vez una onda de agua o una onda electromagnética) que se está lavando sobre ella. Ya que\(φ\) es solo un conteo, es claramente un escalar. Eso significa que tenemos alguna función que toma como entrada un vector\(\to o\) y da como salida el escalar\(φ\). Esta función tiene todas las características adecuadas para ser descrita como una medida\(ω\to o\) de\(\to o\) con algún covector\(ω\to \), y en un estilo constructivo de matemáticas esta es una buena manera de definir un covector: es una función lineal desde el espacio de vectores hasta los números reales. Llamamos\(ω\to \) al covector frecuencia-longitud de onda, o simplemente el covector de frecuencia para abreviar. Si\(\to o\) representa un segundo como se mide en el reloj de este observador, entonces\(ω\to o\) es la frecuencia\(ω\) medida por este observador en unidades de radianes por segundo. Si el mismo observador considera\(s\) que es un vector de simultaneidad con una longitud de un metro, entonces\(ω\to s\) es la medida del observador del número de onda\(k\), definido como\(2π\) dividido por la longitud de onda.

Visualización

Figura\(\PageIndex{1}\): 1. Un vector de desplazamiento. 2. Un covector. 3. La medición se reduce al conteo. El observador, representado por el vector de desplazamiento, cuenta 24 frentes de onda.

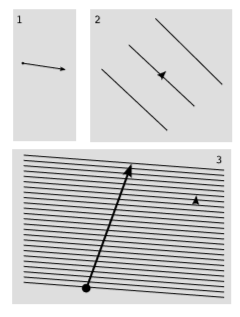
En más de una dimensión, existen formas naturales de visualizar los diferentes espacios vectoriales habitados por vectores y covectores. Un vector es una flecha. Un covector se puede visualizar como un conjunto de líneas paralelas, espaciadas uniformemente en un mapa topográfico,\(\PageIndex{1}\) (2), con una punta de flecha para mostrar qué camino es “cuesta arriba”. El acto de medición consiste en contar cuántas de estas líneas son cruzadas por un determinado vector, figura\(\PageIndex{1}\) (3).

Ejemplo\(\PageIndex{1}\): Parallelism between vectors and covectors

Parece visualmente obvio en la figura\(\PageIndex{1}\) (3), que el vector y el covector son casi, pero no exactamente, paralelos, ya que las puntas de flecha apuntan casi en la misma dirección. Ordinariamente, el paralelismo de vectores distintos de cero\(u\) y se\(v\) expresaría por la existencia de un número real\(α\) tal que\(u = αv\). Pero los vectores y covectores son diferentes tipos de bestias, pertenecientes a diferentes espacios vectoriales. Escalar una cebra nunca producirá una jirafa. Si no hay métrica, entonces esto es simplemente un hecho de la vida: no hay una manera natural de definir el paralelismo entre un vector\(v\) y un covector\(ω\).

Pero si tenemos una métrica, entonces podemos definir una magnitud para el vectorc en la figura\(\PageIndex{1}\) (3), y mantener esa magnitud constante mientras gira\(v\). Si la métrica es euclidiana, entonces esto corresponde a rotar rígidamente la flecha en la página, y\(ω\to v\) se maximiza para una cierta orientación, que definimos como la condición para el paralelismo. Si la métrica no es oneúclida, entonces las cosas se complican un poco más, pero se aplican las mismas ideas si los vectores son ambos espaciales o ambos parecidos al tiempo. Por ejemplo, si ambos son similares al tiempo, entonces\(ω\to v\) se minimiza por el paralelismo, porque la desigualdad Cauchy-Schwarz se invierte (ver sección 1.5)

El Gradiente

Dado un campo escalar\(φ\), su gradiente\(∇φ\) en cualquier punto dado es un covector. El covector de frecuencia es el gradiente de la fase. En notación de huellas de pájaros, indicamos esto escribiéndolo con una flecha que apunta hacia afuera,\((∇φ)\). Debido a que los gradientes ocurren con tanta frecuencia, la notación de las pistas de aves tiene una taquigrafía especial para ellos, que es simplemente un círculo:

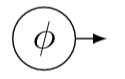
Esta notación también se puede extender al caso donde la cosa que se está diferenciando no es un escalar, sino que luego se encuentran algunas complicaciones cuando las coordenadas no son Minkowski; ver Sección 9.4.

Ejemplo\(\PageIndex{2}\): Cosmological observers

El tiempo es relativo, entonces, ¿qué quiere decir la gente cuando dice que el universo tiene\(13.8\) mil millones de años? Si un hipotético observador hubiera existido desde poco después del big bang, el tiempo transcurrido en el reloj de ese observador dependería de la línea mundial del observador. Dos de esos observadores, que tenían diferentes líneas mundiales, podrían tener lecturas de reloj diferentes.

Los cosmólogos modernos no son ingenuos sobre la dilatación del tiempo. Tienen en mente una línea mundial cosmológicamente preferida para su observador. Una forma de construir esta línea mundial es la siguiente. Con el tiempo, la temperatura\(T\) del universo ha disminuido. (Definimos esta temperatura localmente, pero promediamos en regiones lo suficientemente grandes para que las variaciones locales no importen). El gradiente negativo de esta temperatura,\(-∇T\), es un covector que apunta en una dirección preferida en el espacio-tiempo, y una línea mundial preferida para un observador es aquella cuyo vector de velocidad\(v\) es siempre paralelo a\(-∇T\), en el sentido definido en el ejemplo\(\PageIndex{1}\) anterior.