6.5: El desplazamiento Doppler y la aberración
- Page ID
- 126628
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Objetivos de aprendizaje
- Qué es la aberración
Desplazamientos Doppler
Como ejemplo, generalizamos nuestra discusión previa sobre el desplazamiento Doppler de la luz a\(3 + 1\) las dimensiones.
Para mayor claridad, primero mostremos cómo funciona el caso\(1+1\) -dimensional en nuestra nueva notación. Para una ola que viaja hacia la izquierda, tenemos\(ω\to = (ω,ω)\) (no\((ω,-ω)\) — ver figura 6.6.1 (1). Ahora queremos transformarnos en el marco de un observador que se mueve hacia la derecha con velocidad\(v\) relativa al cuadro original. Porque\(ω\to \) es un covector, lo hacemos usando la transformación inversa de Lorentz. Una transformación ordinaria de Lorentz tomaría un vector similar\((ω,ω)\) a la luz\((ω/D,ω/D)\) (ver sección 3.2). La transformación inversa de Lorentz da\((Dω,Dω)\). La frecuencia ha sido desplazada hacia arriba por el factor\(D\), como se estableció previamente.
En\(3 + 1\) dimensiones, un plano espacial está determinado por la dirección de propagación de la luz y la velocidad relativa de la fuente y el observador, por lo que este caso se reduce sin pérdida de generalidad a\(2 + 1\) las dimensiones. El cuatro vector de frecuencia debe ser similar a la luz, por lo que su forma más general posible\(θ\) es\((ω,ω cosθ,ω sinθ)\), donde se interpreta como el ángulo entre la dirección de propagación y la velocidad relativa. En\(2+1\) dimensiones, un impulso de Lorentz a lo largo del eje\(x\) - se ve así:
\[t' = \gamma t - v\gamma x\]
\[x' = - v\gamma t + \gamma x\]
\[y' = y\]
La transformación inversa se encuentra al flipping el signo de\(v\). Poniendo nuestro vector de frecuencia a través de un impulso inverso de Lorentz, encontramos
\[\omega ' = \gamma \omega (1 + v\cos \theta )\]
Para\(θ = 0\) el factor Doppler reduce a
\[γ(1+v) = D\]
que recupera el resultado\(1 + 1\) -dimensional. Porque\(\theta = 90^{\circ}\), tenemos\(ω' = γω\), que se interpreta como un puro efecto de dilatación del tiempo cuando el movimiento de la fuente es transversal a la línea de visión.
Para ver el poder de las herramientas matemáticas que hemos desarrollado en este capítulo, es posible que desee ver las secciones 6 y 7 del artículo de Einstein sobre relatividad especial de 1905, donde se necesita una larga derivación para llegar al mismo resultado.
Aberración
Imagina que la lluvia cae verticalmente mientras conduces en un descapotable con la parte superior hacia abajo. Para ti, las gotas de lluvia parecen estar moviéndose en algún ángulo distinto de cero en relación con la vertical. Esto se conoce como aberración.
Definición: aberración
La dirección de una línea mundial cambia dependiendo del marco de referencia.
En el marco de referencia de la calle, el ángulo entre las tres velocidades de la lluvia y la del auto es\(\theta = 90^{\circ}\), pero en el marco del auto\(\theta ' \neq 90^{\circ}\). En este ejemplo, la aberración es un gran efecto porque la velocidad del automóvil\(v\) es comparable a la velocidad\(u\) de las gotas de lluvia. A un caracol que se arrastra por la acera a un nivel mucho más bajo\(v\), el efecto sería pequeño. Usando la aproximación de ángulo pequeño\(\tan \epsilon \approx \epsilon\), encontramos que para pequeños\(v\), la diferencia\(∆θ = θ' - θ\) sería aproximadamente\(v/u\), en unidades de radianes.
Comparado con un rayo de luz, todos somos como caracoles. Por ejemplo, la velocidad orbital de la tierra es aproximadamente\(v ∼ 10^{-4}\) en unidades donde la velocidad de la luz\(u = 1\), por lo que esperamos un efecto máximo de aproximadamente\(10^{-4}\) radianes, o\(2'' \) de arco, que es pequeño pero no despreciable para un telescopio con montura de alta calidad, siendo utilizado a gran aumento.
Esta estimación de la aberración astronómica de la luz es más o menos correcta, pero no esperamos que sea exacta, tanto por la aproximación de ángulo pequeño como porque la calculamos usando una imagen galilea del espacio-tiempo. Calculemos el resultado exacto. Como se muestra en el Ejemplo 6.6.1, la dirección de propagación de una onda de luz se encuentra a lo largo del vector que es el dual a su covector de frecuencia. Llamemos a esta dirección de propagación\(\to u\). Reutilizando la expresión para\(ω\to \) definido anteriormente, y fijando arbitrariamente\(\to u\) el componente timelike para ser\(1\), tenemos
\[\to u = (1,-\cos\theta ,-\sin\theta )\]
Cuando este vector sufre un impulso\(v\) a lo largo del eje\(x\) - se convierte en
\[\to u' = \left ( \gamma (1 + v\cos \theta ), \gamma (-v - v\cos \theta ), -\sin \theta \right )\]
El ángulo original
\[\theta = \tan^{-1}\frac{u_y}{u_x}\]
se ha transformado a
\[\theta ' = \tan^{-1}\frac{u_y'}{u_x'}\]
siendo el resultado
\[\tan \theta ' = \frac{\sin \theta }{\gamma (\cos \theta + v)}\]
Ejemplo\(\PageIndex{1}\): A test of special relativity
Una suposición subyacente a este tratamiento de aberración fue que la velocidad de la luz era\(u = c\), independientemente de la velocidad de la fuente. No todas las teorías prerelativistas tenían esta propiedad, y cabría esperar que en tal teoría, la aberración no estaría de acuerdo con el resultado relativista. En particular, supongamos que creíamos en el espacio-tiempo galileo, de manera que cuando una galaxia distante, alejándose de nosotros a cierta velocidad\(w\), emitía un rayo de luz hacia nosotros, la velocidad de la luz en nuestro marco lo era\(u = c - w\). Es decir, imaginamos una teoría en la que emitir un rayo de luz es como disparar una bala desde un arma de fuego. Dado que los efectos de aberración van aproximadamente como\(v/u\), esperaríamos que\(u\) lo reducido condujera a más aberración en comparación con la predicción de la relatividad.
Para probar teorías de este tipo, Heckmann 1 utilizó un reflector de\(24\) pulgadas en Hamburgo para tomar placas fotográficas de gran aumento de un campo estelar en la Osa Mayor que contenía\(11\) estrellas dentro de la Vía Láctea y galaxias\(5\) distantes. Las mediciones de los desplazamientos Doppler mostraron que las galaxias estaban retrocediendo de nosotros a velocidades de aproximadamente\(w = 0.05c\), mientras que las estrellas dentro de la Vía Láctea se mueven con relación a nosotros a velocidades que son insignificantes en comparación. Si, contrariamente a la predicción relativista, esto condujera a una\(5\%\) disminución de\(u\), entonces esperaríamos alrededor de un\(5\%\) aumento en la aberración para las galaxias en comparación con las estrellas.
A lo largo de un año, la órbita terrestre la lleva hacia y desde la Osa Mayor, de manera que en el marco de referencia de la tierra, las estrellas y galaxias tienen velocidades variables en relación con nosotros, y el efecto de\(∼20''\) aberración oscila en dirección. Si el efecto era diferente para las galaxias y las estrellas, entonces deberían cambiar sus posiciones aparentes una respecto a la otra. El cambio debe ser del orden\(5\%\) de\(2000\), o un segundo de arco. Los resultados de las observaciones mostraron que estas posiciones relativas no parecieron variar en absoluto a lo largo de un año, siendo el desplazamiento relativo promedio\(0.00±0.06''\) de arco. Esta diferencia en la aberración es consistente con cero, como lo predice la relatividad especial.
Ejemplo\(\PageIndex{2}\): The view of an ultrarelativistic observer
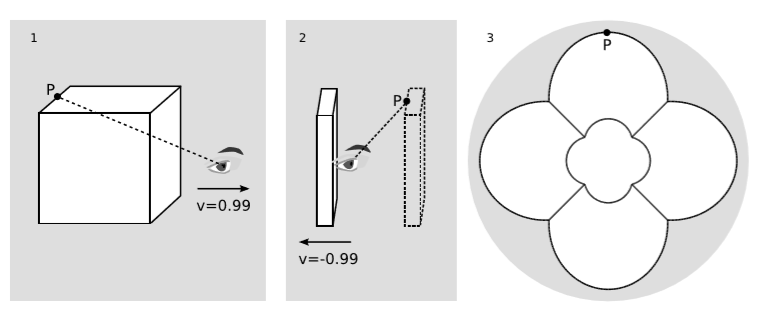
La figura\(\PageIndex{1}\) muestra una visualización para un observador que flota a través de un cubo en\(v = 0.99\). En la figura\(\PageIndex{1}\) (1), el cubo se muestra en su propio marco de reposo, donde tiene lados de longitud unitaria, y el observador, habiendo pasado ya por él, yace una unidad a la derecha del centro del cubo. El observador está mirando hacia la derecha, lejos del cubo. La línea discontinua es un rayo de luz que viaja de punto\(P\) a observador, y en este marco aparece como si el rayo, que llega de\(\theta = 162^{\circ}\), no lo haría en el ojo del observador.
Pero en el marco del observador, figura\(\PageIndex{1}\) (2), el rayo está en\(\theta ' = 47^{\circ}\), por lo que en realidad sí cae dentro de su campo de visión. El cubo está contraído en longitud por un factor\(γ ≈ 7\). El rayo se emitió antes, cuando el cubo estaba afuera frente al observador, en la posición mostrada por el contorno discontinuo.
La imagen vista por el observador se muestra en la figura\(\PageIndex{1}\) (3). El contorno circular que define el campo de visión representa\(\theta ' = 50^{\circ}\). Tenga en cuenta que la contracción relativista de longitud no es en absoluto lo que un observador ve ópticamente. La observación óptica está influida por la contracción de la longitud, pero también por la aberración y por el tiempo que tarda la luz en propagarse al observador. El tiempo de propagación es diferente para diferentes partes del cubo, por lo que en el cuadro del observador, figura\(\PageIndex{1}\) (2), se tuvieron que emitir rayos de diferentes puntos cuando el cubo estaba en diferentes puntos de su movimiento, si esos rayos llegaran al ojo.
Un grupo de la Universidad Nacional de Australia ha producido animaciones de escenas similares, que se pueden encontrar en línea buscando “efectos ópticos de relatividad especial”.
El video muestra representaciones fotorrealistas de escenas de c. reducidas. Esto significa que la velocidad de la luz se ha ralentizado de más de mil millones de kilómetros por hora a una velocidad de sólo un metro por segundo. Las consecuencias de esta ficción se han restringido a los efectos ópticos, y nos permite ver efectos especiales-relativistas que no son posibles en la vida cotidiana.
Es divertido imaginar la vista de un observador a bordo de una nave espacial ultrarelativista. Para\(v\) suficientemente cerca de\(1\), cualquier ángulo\(\theta < 180^{\circ}\) se transforma en un pequeño\(θ'\). Así, toda la luz que llega a este observador desde las estrellas circundantes, ¡incluso las que están en direcciones extremas hacia atrás! — se reúne en un pequeño y brillante parche de luz que parece provenir de adelante recto. Algo de luz visible se desplazaría hacia los extremos ultravioleta e infrarrojo, mientras que algo de luz infrarroja y ultravioleta se volvería visible.


