6.6: Velocidad de fase y grupo

Objetivos de aprendizaje

• Explicar la velocidad de fase y velocidad de grupo

Velocidad de fase

Un frente de onda es una línea o superficie de fase constante. En una instantánea de una onda en un momento, la dirección de propagación de la onda es a través de los frentes de onda. La situación visual es diferente en un diagrama de espacio-tiempo.

Figura\(\PageIndex{1}\): El surfista se mueve directamente a la derecha con vector de velocidad\(u\). La ola también se propaga hacia la derecha.

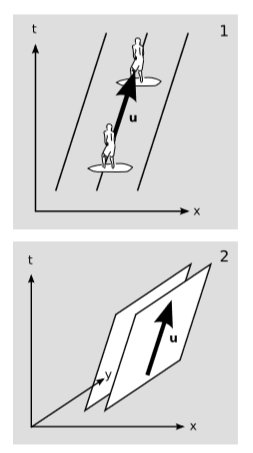
En\(1 + 1\) dimensiones, figura\(\PageIndex{1}\) (1), supongamos que las líneas representan la cresta de las olas de agua. El surfista está encima de una cresta, cabalgando junto con él. Su vector de velocidad\(u\) está en la dirección espacio-tiempo que se encuentra en la parte superior del frente de onda, no a través de él. Claramente tanto su movimiento como la propagación de la ola están a la derecha, no a la izquierda como podríamos imaginar a partir de la experiencia con instantáneas de olas.

En\(2+1\) dimensiones,\(\PageIndex{1}\) (2), la velocidad del surfista se visualiza como una flecha que se encuentra dentro de un plano de fase constante. Dada la información de fase de la onda, hay más de una flecha posible de este tipo. Podríamos tratar de resolver la ambigüedad exigiendo que la proyección de la flecha hacia el\(xy\) plano sea perpendicular a la intersección de los frentes de onda con ese plano, pero (con la excepción del caso donde la onda viaja en\(c\), Ejemplo\(\PageIndex{1}\)) esta prescripción da resultados que cambiar dependiendo de nuestro marco de referencia, y los cambios no son descriptibles por una transformación Lorentz del vector de velocidad. Esto demuestra que en el caso general, la información de fase de la onda, codificada en el covector de frecuencia\(ω\to \), no describe la dirección de la propagación de la onda a través del espacio. A lo sumo nos dice la velocidad de fase de la onda\(ω/k\), que en realidad no es una velocidad. Todos estos son síntomas del hecho de que una velocidad se supone que es un vector, pero\(ω\to \) es un covector. La velocidad de fase carece de interés físico, porque no es la velocidad a la que se mueve ninguna “cosa”.

Vector de velocidad de una onda de luz, dada su fase

Hemos visto que en general, la información sobre la fase de una onda codificada en\(ω\to \) no determina su dirección de propagación. La excepción es una onda, como una onda de luz, que se propaga en\(c\). Deje que una línea mundial de propagación de la onda se encuentre a lo largo del vector\(\to v\). En el caso de una onda que se propaga a\(c\), tenemos\(v^2 = 0\) (de modo que no\(\to v\) puede tener la normalización habitual para un vector de velocidad), y la relación de dispersión es simplemente\(ω^2 = 0\). Dado que la fase se mantiene constante a lo largo de una línea mundial de propagación,\(ω\to v = 0\). Por lo tanto, encontramos que\(v\) y\(ω\) son dos vectores distintos de cero, parecidos a la luz, que son ortogonales entre sí. Pero como se muestra en el problema Q10 en el capítulo 1, esto implica que los dos vectores son paralelos. Así, si nos dan el covector\(ω\to \), solo tenemos que computar su dual\(\to ω\) para encontrar la dirección de propagación.

Velocidad de grupo

La velocidad de fase no es la velocidad a la que “cosas” es transmitida por la onda. La velocidad de las cosas se llama la velocidad del grupo. Para tener una velocidad de grupo definida de manera significativa, necesitamos tener una onda que se modula, porque una onda no modulada es una onda sinusoidal infinita que se extiende hasta el infinito, y tal onda no modulada no transmite ninguna energía o información. Una onda no modulada tiene el mismo covector de frecuencia\(ω\to \) en todo el espacio-tiempo, es decir, la misma frecuencia\(ω\) y número de onda\(k\). Una forma de describir una onda modulada es por cómo\(ω\to \) cambia.

Figura\(\PageIndex{2}\): Los puntos de la gráfica satisfacen la relación de dispersión\(C = 0\) para las olas de agua. En un punto dado de la gráfica, el covector nos\((∇C)\) dice la velocidad del grupo.

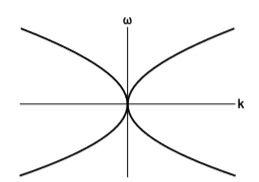
Pero los diferentes componentes de no\(ω\to \) son libres de cambiar de ninguna manera elegida al azar. Normalmente están constreñidos por una relación de dispersión. Por ejemplo, las ondas superficiales en aguas profundas obedecen a la restricción\(C = 0\), donde\(C = ω^4 - α^2k^2\) (figura\(\PageIndex{2}\)) y\(α\) es una constante con unidades de aceleración, relativa a la aceleración de la gravedad. (Dado que el agua es infinitamente profunda, no hay otra escala que pueda entrar en la restricción).

Ahora bien, si cierto bache en la envolvente con la que se modula la onda visita eventos espacio-tiempo\(P\) y\(Q\), entonces cualquier frecuencia y longitud de onda que tenga la onda cerca del bache se observa que son las mismas en\(P\) y\(Q\). En general,\(k\) y\(ω\) son constantes a lo largo del desplazamiento espacio-tiempo de cualquier punto de la envolvente, por lo que el desplazamiento espacio-tiempo\(\to r\) de\(P\) a\(Q\) debe satisfacer la condición\((∇ω)\to r = 0\).

Además,\(∇ω\) debe ser tangente a la superficie de restricción\(C = 0\), de manera que la onda siempre obedezca a la restricción. Por lo tanto, dado un punto\(ω\to \) en el espacio de frecuencia, la dirección de propagación\(r\) debe ser determinada de manera única por la restricción. Supongamos que\(C\) es una función de buen comportamiento, de modo que es aproximadamente una función lineal de cualquier pequeño cambio\(∆ω\), es decir, en\(1 + 1\) las dimensiones que tenemos

\[\Delta C = \frac{\partial C}{\partial \omega }\Delta \omega + \frac{\partial C}{\partial k}\Delta k\]

En esta aproximación,\(∆C\) es una función lineal que actúa sobre un covector\(∆ω\) y devuelve un escalar. En otras palabras,\(∆C\) actúa como un vector con componentes

\[\Delta C = \left ( \frac{\partial C}{\partial \omega }, \frac{\partial C}{\partial k} \right )\]

Este vector es paralelo a\(r\), de manera que apunta en la dirección de propagación de la onda a través del espacio-tiempo, y nos dice su velocidad de grupo\(\left ( \tfrac{\partial C}{\partial k} \right )/ \left ( \tfrac{\partial C}{\partial \omega } \right )\). En nuestro ejemplo de olas de agua, un cálculo muestra que la velocidad del grupo es\(±α/2ω\), que es la mitad de la velocidad de fase.