8.1: Marcos Giratorios de Referencia
- Page ID
- 126548
Objetivos de aprendizaje
- Explicar el sistema de coordenadas de rotación y rotación
Sin sincronización de reloj
Los paneles 1 y 2 de la figura\(\PageIndex{1}\) recapitulan el resultado del Ejemplo 1.4.6. El conjunto de tres relojes fijados a la tierra en\(\PageIndex{1}\) (1) han sido sincronizados por la sincronización de Einstein (Ejemplo 1.1.4), es decir, mediante el intercambio de fletes de luz. Los tres relojes a bordo del tren en movimiento,\(\PageIndex{1}\) (2), se han sincronizado de la misma manera, y los eventos que fueron simultáneos según el cuadro 1 no son simultáneos en el cuadro 2. Hay un desplazamiento sistemático en los tiempos, que se representa por el término\(t' = ... - vγx\) en la transformación de Lorentz (Ecuación 1.4.1).
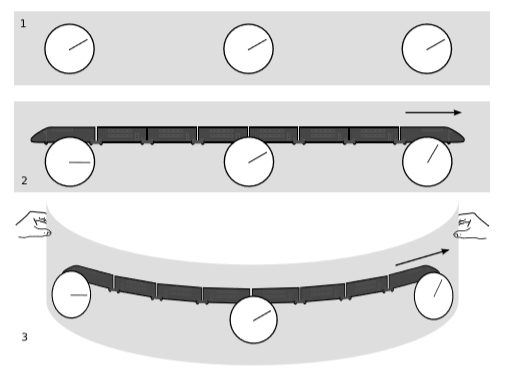
Ahora supongamos que tomamos el diagrama del tren y lo envolvemos,\(\PageIndex{1}\) (3). Si seguimos y cerramos el bucle, convirtiendo la cadena en un círculo como un collar de cadena, tenemos un problema. La tendencia en los tiempos del reloj puede continuar hasta que se vuelva a dar vueltas al principio, pero luego habrá una discrepancia.
Concluimos que los relojes no se pueden sincronizar en un marco de referencia giratorio. Tal trama no admite una coordenada de tiempo universal porque la sincronización de Einstein no es transitiva: sincronizar el reloj A con el reloj B, y B con C, no implica que A esté sincronizada con C. Esta no transitividad es una forma de definir lo que entendemos por rotación. Es decir, si la definición operativa de un marco inercial dada en la sección 5.1, muestra que nuestro marco es no inercial, y queremos saber más sobre por qué es no inercial, probar esta no transitividad es una forma de averiguar si es por rotación.
La rotación es detectable localmente
Las personas a bordo del tren circular saben que sus intentos de sincronización fallan, por lo que pueden decir, sin referencia a nada externo, que van en círculo.
A pesar de que se trata de un libro sobre relatividad especial, no general, es interesante observar la siguiente posibilidad. Supongamos que verificamos, mediante experimentos locales, que tenemos un buen marco de referencia inercial, no giratorio. Es entonces imaginable que si vemos galaxias distantes desde este marco, las veremos rotar a alguna frecuencia angular\(Ω\) alrededor de algún eje en la esfera celeste. Si esto se observa, entonces debemos inferir que es el universo en su conjunto, ¡no nuestro laboratorio! — es decir, rotar. Tal efecto ha sido buscado y, por ejemplo, un límite superior\(\Omega \lesssim 10^{-7}\) radián/año fue inferido por Clemence. 1 Los modelos general-relativistas de tales cosmologías giratorias tienen un vector preferido que constituye la dirección del eje alrededor del cual gira la materia, pero no existe un centro global de rotación. Los límites superiores de corriente\(Ω\) son lo suficientemente buenos como para descartar cualquier efecto significativo en la expansión cosmológica debido a las fuerzas centrífugas.
El efecto Sagnac
Si bien el escenario del tren es obviamente poco realista, el cambio de tiempo dista mucho de ser hipotético. Este tipo de efecto, denominado efecto Sagnac, fue observado por primera vez por M. Georges Sagnac en 1913, y se relaciona con el principio del giroscopio láser anular (Ejemplo 1.1.4), utilizado en jets de pasajeros. (El nombre es francés, y se pronuncia\ sah-nyahk.”) Para encontrar cuantitativamente el efecto Sagnac, observamos que en el ejemplo del tren circular (ignorando signos) el término relevante en la transformación de Lorentz,\(v\gamma x\), acumularía, después de un circuito completo de sincronización de Einstein, una discrepancia\(\delta\) igual a la circunferencia del círculo multiplicado por\(v\gamma\). Si el radio del círculo es\(r\) y la velocidad angular\(\omega\), tenemos\(\Delta t = 2\pi \gamma r^2\omega\). Esto se puede reescribir en términos del área del círculo\(A\) como\(\Delta t = 2A\omega\), o, reinsertando factores de\(c\) para acomodar unidades SI,\(\Delta t = \frac{2A\omega }{c^2}\). La proporcionalidad al área cerrada no es un accidente; el producto\(vx\) tiene la forma del integrando\(F\cdot ds\) que ocurre en el teorema de Stokes.
Ejemplo\(\PageIndex{1}\): Sagnac effect in the Hafele-Keating experiment
Un reloj en el ecuador de la tierra gira a una frecuencia\(ω\) de\(2π\) radianes por día sideral, sufriendo un efecto Sagnac de\(210\: ns\) por día. Los relojes atómicos itinerantes en el experimento de Hafele-Keating dieron la vuelta al mundo en ambas direcciones, y se compararon con un tercer juego de relojes que se quedaron en Washington, DC. Dado que el tiempo requerido para volar alrededor de la tierra también fue del orden de un día, las diferencias en los valores de\(ω\) para los tres juegos de relojes estaban en el mismo orden de magnitud que el\(ω\) de la tierra, y por lo tanto esperamos efectos diferenciales acumulativos de Sagnac que también están en el orden de cien nano segundos. Estos efectos existen solo en el marco giratorio de la tierra, pero las cosas que se miden son tiempos propios, y el tiempo adecuado es un escalar, por lo que los resultados experimentales son independientes de qué marco de referencia se utiliza para calcularlos. Dado que los pilotos de la aerolínea proporcionaron a Hafele y Keating datos de navegación referidos a la tierra giratoria, analizaron sus resultados en el marco giratorio, en el que hubo un efecto Sagnac. Igualmente bien podrían haber transformado sus datos en el marco de las estrellas, en cuyo caso se habría pronosticado el mismo resultado, pero se habría descrito como derivado de la dilatación cinemática del tiempo.
Ejemplo\(\PageIndex{2}\): Ring laser gyroscope
El giroscopio láser anular en la foto del Ejemplo 1.1.4 parece que tiene un área del orden de\(10^2\: cm^2\) y usa luz roja. Para su uso en la navegación, se quiere poder detectar un cambio en el curso de, digamos, un grado en nuestra hora, o\(ω ∼5×10^{-6}\: radian/s\). El resultado es un cambio de tiempo\(∆t ∼ 10^{-24}\: s\), que para la luz roja es un desplazamiento de fase de solo\(∆φ = 4πAω/cλ ∼3×10^{-9}\) radianes. En los experimentos originales del siglo XIX, este cambio de fase habría tenido que medirse produciendo interferencia entre los dos haces y midiendo el cambio de intensidad resultante de este cambio de fase. Nuestra estimación de\(φ\) muestra que esto no es práctico para un instrumento portátil. En un moderno giroscopio láser de anillo, se inserta un medio láser activo en el bucle, y el resultado es que el bucle resuena a una frecuencia que se desplaza de la frecuencia natural del láser por\(∆f ∼ ∆φc/L\), donde\(L\) está la circunferencia. El resultado es un desplazamiento de frecuencia de unos pocos Hz, que es fácilmente medible. Una técnica alternativa, utilizada en el giroscopio de fibra óptica, es envolver\(N\) giros de fibra óptica alrededor de la circunferencia, cambiando efectivamente\(A\) a\(NA\).
Un sistema de coordenadas giratorias
El sistema GPS es un ejemplo práctico de un caso en el que naturalmente queremos emplear un sistema de coordenadas giratorias. Los excursionistas y marineros, después de todo, quieren saber dónde están en relación con la superficie giratoria de la tierra. Dado que las ubicaciones deben determinarse dentro de los metros, la sincronización de las señales debe hacerse con una precisión de algo así como\((1 m)/c\), que es de unos pocos nanosegundos. Es por ello que los satélites GPS tienen relojes atómicos a bordo, y el tiempo a esta precisión claramente requiere que se tomen en cuenta los efectos relativistas. Por lo tanto, no necesitamos un sistema de coordenadas rotativas newtonianas sino un sistema relativista giratorio. Comencemos con el marco no giratorio, y definamos coordenadas\((t,r,θ,z)\),\((r,θ,z)\) siendo la parte espacial coordenadas cilíndricas ordinarias. Por simplicidad, descuidaremos la\(z\) coordenada en lo que sigue. Extendiendo el resultado del problema Q1 en el capítulo 7 de\(2 + 0\) dimensiones a\(2 + 1\), tenemos la métrica
\[ds^2 = dt^2 - dr^2 - r^2 d\theta ^2\]
Los resultados anteriores muestran que no esperamos poder definir una coordenada de tiempo completamente satisfactoria en el marco giratorio, así que comencemos con el cambio mínimo\((t,r,θ) → (t,r,θ')\), donde\(θ' = θ - ωt\). Esto es al menos suficiente para que las líneas mundiales de constante\(θ'\) sean aquellas que giran alrededor del origen a la frecuencia apropiada. Sustituyendo\(dθ = dθ' + ω dt\), encontramos
\[ds^2 = (1 - \omega ^2r^2)dt^2 - dr^2 - r^2 d\theta '^2 - 2\omega r^2 d\theta 'dt\]
Reconociendo\(ωr\) como la velocidad de un fotograma relativo a otro, y\((1 - ω^2r^2) {-1/2}\) como\(γ\), vemos que sí tenemos un efecto relativista de dilatación del tiempo en el\(dt^2\) término. Pero los\(dθ'^2\) términos\(dr^2\) y tienen el mismo aspecto que en Ecuación\(\PageIndex{1}\). ¿Por qué no vemos ninguna contracción Lorentz de la escala de longitud en la dirección acimutal?
La respuesta es que las coordenadas en la relatividad son arbitrarias, y solo porque podamos anotar cierto conjunto de coordenadas, eso no significa que tengan ninguna interpretación física especial. Las coordenadas\((t,r,θ')\) no corresponden físicamente a las cantidades que un observador giratorio\(R\) mediría con relojes y métricas. Si\(R\) usa una regla para medir un arco corto a lo largo de la circunferencia del círculo\(r = r'\), la distancia es una distancia que se mide entre eventos en espacio-tiempo que son simultáneos en el resto del cuadro de la regla, y estos no ocurren en el valor de tiempo de la coordenada de tiempo\(t\). En la transformación de Lorentz, para el movimiento lineal, es el\(-vγx\) término aplicado a los tiempos el que soluciona estos problemas y hace que t0 represente adecuadamente la simultaneidad en el nuevo fotograma. En nuestra versión rotacional, podríamos intentar hacer algo similar definiendo una coordenada de tiempo\(t' = t + fθ'\), donde\(f\) es una función de\(r\) que está diseñada para que el término\(dθ'dt\) cruzado en la métrica desaparezca. Esto se puede hacer (la función\(f\) que funciona resulta ser\(ωr^2/(1 - ω^2r^2)\)), pero el problema es que la\(t'\) coordenada no es de un solo valor, en el sentido de que\((t,r,θ)\) y no\((t,r,θ + 2π)\) produciría lo mismo\(t'\). Esto es inevitable, como hemos visto en el inicio de esta sección, por lo que no podemos mejorar las coordenadas\((t,r,θ')\) y la métrica (Ecuación\(\PageIndex{2}\)).
Las coordenadas\((t,r,θ')\), con la métrica (Ecuación\(\PageIndex{2}\)) son las utilizadas en el sistema GPS, y en ese contexto se denominan coordenadas inerciales centradas en la Tierra (ECI). (Otro nombre es Born coordinates.) Su coordenada de tiempo no es el tiempo medido por un reloj en el marco giratorio, sino simplemente la coordenada de tiempo del marco de referencia no giratorio vinculado al centro de la tierra. Conceptualmente, podemos imaginar esta coordenada temporal como una que se establece enviando una señal electromagnética de “tic-tac” desde el centro de la tierra, con cada satélite corrigiendo la fase de la señal en función del tiempo de propagación inferido de la suya propia\(r\). En realidad, esto se logra mediante la comunicación con una estación maestra de control en Colorado Springs, que se comunica con los satélites a través de relés en Kwajalein, Isla Ascensión, Diego García y Cabo Cañaveral.