10.6: Tensor de tensión-energía del campo electromagnético

Objetivos de aprendizaje

• Explicar el tensor de tensión-energía para el campo electromagnético

El campo electromagnético tiene asociado un tensor de tensión-energía. De nuestro estudio del electromagnetismo sabemos que el campo electromagnético tiene densidad de energía\(U=(E^2+B^2)/8\pi k\) y densidad de momento\(\vec{S}=(\vec{E}\times\vec{B})/4\pi k\) (en unidades donde\(c=1\), con\(k\) ser la constante de Coulomb). Esto corrige los componentes del tensor de tensión-energía de la forma\(T^{t\ldots}\) y\(T^{\ldots t}\), es decir, la fila superior y la columna izquierda, para que se vean así:

\[T^{\mu\nu} = \begin{pmatrix} U & S_x & S_y & S_z \\ S_x & & & \\ S_y & & & \\ S_z & & & \end{pmatrix}\]

Figura\(\PageIndex{1}\): Presión y tensión en campos electrostáticos.

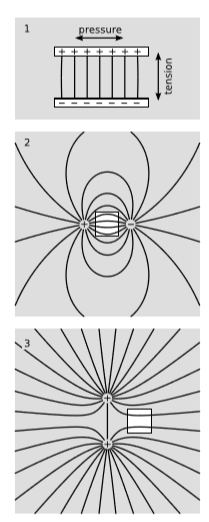
El siguiente argumento nos dice algo sobre qué esperar de los componentes\(T^{xx}\),\(T^{yy}\), y\(T^{zz}\), que se interpretan como presiones o tensiones, dependiendo de sus signos. En la figura\(\PageIndex{1}\) (1), las placas del condensador quieren colapsar una contra la otra en la dirección vertical (\(y\)), pero al mismo tiempo las repulsiones internas dentro de cada placa hacen que esa placa quiera expandirse en la\(x\) dirección. Si el condensador está construido con materiales que mantienen su forma, entonces la tensión electromagnética adentro\(T^{yy}<0\) es contrarrestada por la presión\(T^{yy}>0\) en los materiales, mientras que la presión electromagnética\(T^{xx}>0\) es cancelada por la tensión de los materiales\(T^{xx}<0\). Obtuvimos estos resultados para una situación física particular, pero la relatividad requiere que el estrés-energía se defina en cada punto con base en los campos en ese punto, por lo que nuestras conclusiones deben sostenerse en general. En la figura\(\PageIndex{1}\) (2) y la figura\(\PageIndex{1}\) (3), se han dibujado cajas blancas en regiones donde el campo total es fuerte y los campos interactúan fuertemente. En la figura\(\PageIndex{1}\) (2), hay tensión en la\(x\) dirección y presión en\(y\); se puede pensar que la tensión contribuye a la atracción entre las cargas opuestas. En 3, también hay\(x\) tensión y\(y\) presión; la presión contribuye a la repulsión de las cargas similares.

Para que esto sea más cuantitativo, considere la discontinuidad\(E_y\) en la placa superior en la figura\(\PageIndex{1}\) (1). El campo cambia abruptamente desde\(0\) el exterior a algún valor\(E\) entre las placas. Por ley de Gauss, el cargo por unidad de área en la placa debe ser\(\sigma=E/4\pi k\). El campo promedio que experimenta la carga en la placa es\(\overline{E}=(0+E)/2=E/2\), por lo que la fuerza por unidad de área, es decir, la tensión en el campo, lo es\(\sigma \overline{E}=E^2/8\pi k\). Así esperamos\(T^{yy}=-E^2/8\pi k\) si\(E\) está a lo largo del\(y\) eje.

Para el lector que quiera la derivación completa de los nueve componentes restantes del tensor, ahora damos un argumento que hace uso de la siguiente lista de sus propiedades. Otros lectores pueden saltar adelante a donde se presenta el tensor completo.

1. \(T\)es simétrico,\(T^{µν} = T^{νµ}\).
2. Los componentes deben ser de segundo orden en los campos, por ejemplo, podemos tener términos como\(E_xB_z\), pero no\(E_{x}^{3} B_{z}^{7}\) o\(E_xB_zB_y\). Esto se debe a que las ecuaciones de Maxwell son lineales, y cuando una ecuación de onda es perfectamente lineal, la expresión de energía correspondiente es de segundo orden en la amplitud de la onda.
3. \(T\)tiene las propiedades de paridad descritas en el Ejemplo 9.2.3.
4. Los campos eléctrico y magnético se tratan simétricamente en las ecuaciones de Maxwell, por lo que deben tratarse simétricamente en el tensor de tensión-energía. Por ejemplo, podríamos tener un término como\(7E_{x}^{2} + 7B_{z}^{2}\), pero no\(7E_{x}^{2} + 6B_{z}^{2}\).
5. En la sección 9.2, vimos que la condición de energía traza\(T^a\: _a \geq 0\) es satisfecha por una nube de polvo si y sólo si la masa-energía del polvo no se transporta a una velocidad mayor que\(c\). En la sección 4.1, vimos que todas las partículas ultrarelativistas tienen las mismas propiedades mecánicas. Dado que una nube de polvo, en el límite donde se acerca su velocidad\(c\), se encuentra en el borde del límite establecido por la condición de energía traza,\(T^a\: _a \rightarrow 0\), esperamos que el campo electromagnético, en el que se propagan las perturbaciones\(c\), también debe saturar exactamente la condición de energía traza, de manera que \(T^a\: _a = 0\).
6. El tensor tensión-energía debe comportarse adecuadamente bajo rotaciones, lo que básicamente significa eso\(x\)\(y\),, y\(z\) debe tratarse simétricamente.
7. Una onda plana electromagnética que se propaga en la\(x\) dirección no debe ejercer ninguna presión en las\(z\) direcciones\(y\) o.
8. Si el campo obedece las ecuaciones de Maxwell, entonces la condición de conservación de energía\(\frac{\partial T^{ab}}{\partial x^a} = 0\) debería mantenerse.

Estos hechos son suficientes para determinar completamente la forma de los nueve componentes restantes del tensor de tensión-energía. La propiedad 3 requiere que todos estos componentes estén incluso bajo paridad. Dado que los campos eléctricos se voltean bajo paridad pero los campos magnéticos no (Ejemplo 10.3.1), estos componentes solo pueden tener términos como\(E_i E_j\) y\(B_i B_j\), no términos mixtos como\(E_i B_j\). Teniendo en cuenta las propiedades 4 y 6, encontramos que los términos diagonales deben verse como

y los fuera de la diagonal

Propiedad 5 da\(1/2-a-3b=0\) y 7 da\(b=-a/2\), así que tenemos\(a=-1\) y\(b=1/2\). La determinación de\(c=-1\) se deja como ejercicio, problema Q4.

Ahora hemos establecido la expresión completa para el tensor de tensión-energía del campo electromagnético, que es

donde

y\(\sigma\), conocido como el tensor de estrés Maxwell, viene dado por

Todo esto se puede expresar de manera más compacta y de una manera independiente de las coordenadas como

\[T^{ab} = \frac{1}{4\pi k} \left(\mathcal{F}^{ac}\mathcal{F}^b\: _c + \frac{1}{4}o^do_dg^{ab}\mathcal{F}_{ef}\mathcal{F}^{ef}\right)\]

donde\(\vec{o}\) es un vector de velocidad dirigido al futuro, de manera que\(o^do_d=+1\) para la firma\(+---\) utilizada en este libro, y\(-1\) si la firma es\(-+++\).

Ejemplo\(\PageIndex{1}\): Stress-energy tensor of a plane wave

Dejar que una onda plana electromagnética (no necesariamente sinusoidal) se propague a lo largo del\(x\) -eje, con su polarización tal que\(\vec{E}\) esté en la\(y\) dirección y\(\vec{B}\) en el\(z\) eje, y\(|\vec{E}| = |\vec{B}| = A\). Entonces tenemos lo siguiente para el tensor estres-energía.

\[T^{\mu \nu } = \frac{A^2}{4\pi k} \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

El\(T^{tt}\) componente nos dice que la onda tiene una cierta densidad de energía. Debido a que la onda es sin masa, la tenemos\(E^2 - p^2 = m^2 = 0\), por lo que la densidad de impulso es la misma que la densidad de energía, y\(T^{tx}\) es la misma que\(T^{tt}\). Si esta ola golpea una superficie en el\(yz\) plano, el impulso que la superficie absorbe de la ola se sentirá como una presión, representada por\(T^{xx}\).

En el límite ultrarelativista\(v →1\), esto se convierte en

\[T^{\mu \nu } = \text{(energy density)} \times \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

que es exactamente el mismo que el resultado de nuestra onda electromagnética. Esto ilustra el hecho discutido en la sección 4.1 de que todas las partículas ultrarelativistas tienen las mismas propiedades mecánicas.

Ejemplo\(\PageIndex{2}\): Mass of a capacitor

Figura\(\PageIndex{2}\): Masa de un condensador.

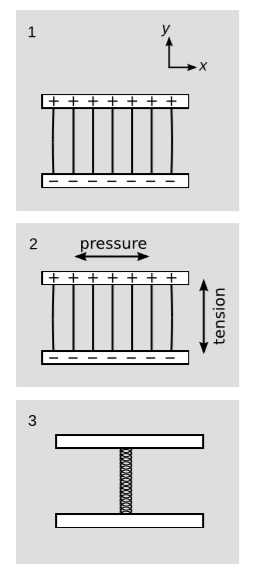
Considere la masa de un condensador de placa paralela cargado, figura\(\PageIndex{2}\) (1), primero en su bastidor de reposo y luego en un bastidor potenciado en la dirección paralela al campo (perpendicular a las placas). Si no tenemos cuidado, nos encontramos con la siguiente paradoja. Bajo un impulso, un campo eléctrico paralelo al impulso se mantiene sin cambios. Por lo tanto, en el marco potenciado, tenemos exactamente la misma fuerza de campo, pero llenando un volumen que ha sido disminuido por la contracción de la longitud. Por lo tanto, la masa-energía del condensador es mayor en su propio marco de descanso, lo cual es absurdo y contradicería nuestra prueba en la sección 9.3 de que el impulso energético de un sistema aislado se transforma como un cuatro vectores.

Ahí la solución de la paradoja viene de reconocer que asumimos que el condensador estaba en equilibrio estático, pero ignoramos la tensión-energía de cualquier soporte mecánico que estuviera manteniendo este equilibrio. Si consideramos únicamente la tensión-energía\(T_{(em)}\) del campo electromagnético, entonces tenemos\(T_{(em)}^{tt} = \frac{1}{8\pi k}E^2\) (densidad de energía) y\(T_{(em)}^{yy} = -\frac{1}{8\pi k}E^2\) (tensión en la\(y\) dirección, paralela al campo), figura\(\PageIndex{2}\) (2). Es fácil ver que esto tiene una divergencia que no se desvanece, ya que\(\partial _y T_{(em)}^{yy} \neq 0\) en las placas, y no hay otros términos en el tensor de tensión-energía que puedan compensar esto.

Aquí no hay nada sorprendente; sólo el tensor total de energía-estrés\(T\) tiene que ser invariable, no\(T_{(em)}\). Violaría las leyes de la física si el condensador permaneciera en equilibrio así sin alguna fuerza para contrarrestar la tensión electromagnética. Digamos que esta fuerza es proporcionada por un resorte, como en la figura\(\PageIndex{2}\) (3). La primavera tiene su propia contribución\(T_{(s)}\) al estrés-energía. Para mayor comodidad, imaginemos hacer el resorte lleno (en lugar de un cilindro hueco) y engordarlo para que llene todo el volumen interior del condensador. Entonces para lograr el equilibrio estático en el marco de descanso, necesitamos la presión en el resorte para cancelar la presión en el campo eléctrico. Por lo tanto, tenemos\(T^{yy} = 0\) para el tensor total de tensión-energía.

Si ahora aplicamos la ley de transformación del tensor al tensor de energía de estrés, encontramos que el tensor de energía de estrés en el marco potenciado contiene una densidad masa-energía\(T^{t't'}\) que depende solo de\(T^{tt}\) y\(T^{yy}\). (También tiene que haber un\(xx\) componente para evitar que las placas exploten lateralmente, pero eso no entra aquí). Pero tenemos\(T^{yy} = 0\), así que el problema es exactamente lo mismo que transformar un bulto de materia no relativista, y sabemos que ese cálculo sale bien. Para una demostración explícita de que esto todavía funciona si dejamos caer la suposición simplificadora de que el resorte llena todo el volumen interior del condensador, ver Rindler y Denur, “Una simple paradoja relativista sobre la energía electrostática”, Am J Phys 56 (1988) 9.