10.7: Ecuaciones de Maxwell

Objetivos de aprendizaje

• Explicar las ecuaciones de Maxwell

Declaración e interpretación

En este libro supongo que has tenido la formación física habitual adquirida en un curso de encuesta de primer año, que incluye un encuentro inicial, probablemente aterrador, con las ecuaciones de Maxwell en forma integral. En unidades con\(c=1\), las ecuaciones de Maxwell son:

Ecuación de Maxwell

\[\Phi_E = 4\pi kq\]

\[\Phi_B = 0\]

\[\oint \vec{E}\cdot dl = -\frac{\partial \Phi _B}{\partial t}\]

\[\oint \vec{B}\cdot dl = \frac{\partial \Phi _E}{\partial t} + 4\pi kI\]

donde

\[\Phi_E = \int E\cdot da\]

y

\[\Phi_B = \int B\cdot da\]

Ecuaciones\(\PageIndex{1}\) y\(\PageIndex{2}\) se refieren a una superficie cerrada y la carga\(q\) contenida dentro de esa superficie. Ecuación, la ley de Gauss, dice que las cargas son las fuentes del campo eléctrico, mientras que dice que las “cargas” magnéticas no existen. Ecuaciones\(\PageIndex{3}\) y\(\PageIndex{4}\) se refieren a una superficie como una papa chip, que tiene un borde o límite, y la corriente que\(I\) pasa por esa superficie, con las integrales de línea en ser evaluadas a lo largo de ese límite. El lado derecho de dice que un campo magnético cambiante produce un campo eléctrico rizado, como en un generador o un transformador. El\(I\) término en dice que las corrientes crean campos magnéticos que se enrollan a su alrededor. El\(\partial \Phi_E/\partial t\) término, que dice que los campos eléctricos cambiantes crean campos magnéticos, es necesario para que las ecuaciones produzcan resultados consistentes independientemente de las superficies elegidas, y también forma parte del aparato responsable de la existencia de ondas electromagnéticas, en las que el\(\vec{E}\) campo cambiante produce el\(\vec{B}\), y el cambio\(\vec{B}\) hace que el\(\vec{E}\).

Ecuaciones\(\PageIndex{1}\) y no\(\PageIndex{2}\) tienen dependencia del tiempo. Funcionan como restricciones en los posibles patrones de campo. Las ecuaciones\(\PageIndex{3}\) y\(\PageIndex{4}\) son leyes dinámicas que predicen cómo evolucionará un patrón de campo inicial con el tiempo. Se puede demostrar que si\(\PageIndex{1}\) y\(\PageIndex{2}\) están satisfechos inicialmente, entonces\(\PageIndex{3}\) y\(\PageIndex{4}\) asegurar que seguirán siendo satisfechos más adelante. Debido a que las leyes dinámicas consisten en dos ecuaciones vectoriales, proporcionan un total de\(6\) restricciones, que son el número necesario para predecir el comportamiento de los\(6\) campos\(E_x\)\(E_y\),\(E_z\),\(B_x\),\(B_y\), y\(B_z\). <% end_sec ('sentencia maxwell-')

Soporte Experimental

Antes del artículo de Einstein sobre la relatividad de 1905, las leyes conocidas de la física eran las leyes de Newton y las ecuaciones de Maxwell. Experimentos como el Ejemplo 4.2.3 muestran que las leyes de Newton son solo aproximaciones a baja velocidad. Las ecuaciones de Maxwell son aproximaciones de baja velocidad; por ejemplo, en la sección notamos la evidencia de que los átomos son eléctricamente neutros, de acuerdo con la ley de Gauss\(\PageIndex{1}\), Ecuación\(10^{21}\), a una parte en, aunque los electrones en los átomos típicamente tienen velocidades del orden de\(1-10\%\) de \(c\).

Incompatibilidad con el espacio-tiempo galileo

Las ecuaciones de Maxwell no son compatibles con la descripción galileana del espacio-tiempo (sección 1.1). Si asumimos que las ecuaciones se mantienen en algún marco\(\vec{o}\), y luego aplicamos un impulso galileano, transformando las coordenadas\((t,x,y,z)\) en\((t',x',y',z')=(t,x-vt,y,z)\), nos encontramos con que en frame\(\vec{o}'\) las ecuaciones tienen una forma diferente y más complicada que no se puede simplificar para parecerse a la forma que tenían en \(\vec{o}\). En lugar de escribir el horrible desastre resultante y verificar que no se puede volver a lanzar a la forma más simple, una manera más fácil de probar esto es notar que hay soluciones a las ecuaciones en\(\vec{o}\) que no son soluciones después de un impulso galileo en\(\vec{o}'\), si tratamos de mantener las ecuaciones en el misma forma. Por ejemplo, si una onda de luz se propaga en la\(x\) dirección a velocidad\(c\) en\(\vec{o}\), entonces después de un impulso con\(v=c\), tendríamos una onda de luz en marco\(\vec{o}'\) que estaba quieta. (Este es el experimento de pensamiento de Einstein de conducir junto a una ola de luz en una motocicleta, sección 1.1.) Tal onda violaría la Ecuación\(\PageIndex{3}\), ya que el lado izquierdo sería distinto de cero para una superficie que se encuentra en el\(xy\) plano, pero la derivada del tiempo en el lado derecho sería cero.

No manifiestamente relativista en su forma original

Dado que las ecuaciones de Maxwell no son aproximaciones de baja velocidad y son incompatibles con la relatividad galileana, esperamos con el beneficio de la retrospectiva histórica que sean compatibles con la imagen relativista del espacio-tiempo. Pero cuando se expresan en la forma anterior, tienen dos rasgos, cualquiera de los cuales parece suficiente para hacerlos completamente incompatibles con la relatividad:

1. Parecen describir la acción instantánea a distancia. Por ejemplo, la ley de Gauss\(Φ_E = 4πkq\),, relaciona el campo eléctrico en un lugar (en la superficie cerrada) con la carga eléctrica en otro lugar (dentro de la superficie). Esta estructura no local huele mal relativisticamente, por las razones discutidas en la sección 10.2.
2. Parecen tratar el tiempo y el espacio asimétricamente.

Lo que realmente está sucediendo aquí es que las ecuaciones de Maxwell son como una versión de escrito en crayón sobre una larga tira de papel higiénico. Son completamente relativistas, pero se han escrito en una forma que oculta ese hecho.

El problema de la no localidad,\(i\), puede demostrarse que no es un problema porque las ecuaciones de Maxwell pueden ser reelaboradas en una forma en la que son puramente locales. La idea se muestra en la figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un campo magnético que viola\(Φ_B = 0\).

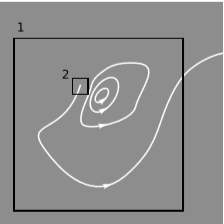
Todas las líneas del campo magnético forman bucles cerrados, a excepción de una de ellas, que comienza en un punto en el espacio y se extiende hasta el infinito. Dibujando la caja grande, 1, encontramos que\(\Phi_{B,1}\), el flujo del campo magnético a través de la caja, no es cero, porque una línea sale de la caja pero ninguna entra. Pero la misma discrepancia podría haberse detectado con la casilla más pequeña 2, o de hecho con una caja arbitrariamente pequeña que contiene la fuente de la línea de campo. En otras palabras, la ecuación\(\Phi_B=0\) es no local, pero si se va a sostener para cualquier superficie, entonces también debe sostenerse localmente, en el límite de una superficie arbitrariamente pequeña. Esta puramente ley de la física puede expresarse utilizando la versión tridimensional de la divergencia, introducida en la sección 9.1:

De las cuatro ecuaciones de Maxwell, ambas ecuaciones\(\PageIndex{1}\) y\(\PageIndex{2}\) pueden ser reexpresadas de esta manera. Este libro no presenta la maquinaria completa del cálculo vectorial ni asume el conocimiento previo del mismo, sino que también se puede aplicar un procedimiento limitante similar a las ecuaciones\(\PageIndex{3}\) y\(\PageIndex{4}\), utilizando un operador llamado el rizo.

El siguiente ejemplo es uno en el que tanto problema como problema resultan no ser problemas.

Ejemplo\(\PageIndex{1}\): Jumping through a hoop

Figura\(\PageIndex{2}\): 1. Un electrón salta a través de un aro. 2. Una superficie alternativa que abarca el aro.

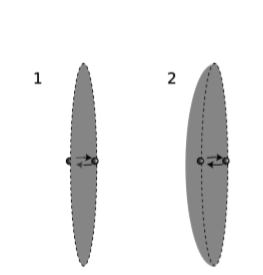
Aquí hay un ejemplo en el que las características no obvias de las ecuaciones de Maxwell impiden la fusión antirelativista proyectada en i. En la figura\(\PageIndex{2}\) (1), un electrón salta de un lado a otro a través de un aro circular imaginario, a través del cual construimos una superficie de flat imaginaria. Cada vez que el electrón perfora la superficie, hace un pico momentáneo en la corriente\(I\), que aparece en:

\[\oint \vec{B}\cdot dl = \frac{\partial \Phi _E}{\partial t} + 4\pi kI\]

Podríamos esperar que esto provoque que el campo\(B\) detectado en el borde del disco muestre picos similares al mismo tiempo. Pero “mismos tiempos” implica alguna noción de simultaneidad, y esto sería incompatible con la relatividad, ya que la coordenada t a la que se hace referencia aquí es solo la noción de tiempo de un observador. Además, parecería que la información se estaba transmitiendo instantáneamente desde el centro del disco hasta su borde, lo que viola la relatividad.

Aún más extraño, podemos producir una aparente paradoja sin siquiera apelar a la relatividad. En lugar de la superficie flat de la figura\(\PageIndex{2}\) (1), podemos escoger una en forma de plato, figura\(\PageIndex{2}\) (2), con una curva lo suficientemente profunda para que el electrón nunca la cruce. La corriente I siempre es cero según esta superficie, de manera que no se\(B\) produciría ningún campo en la llanta en absoluto.

La resolución de todas estas dificultades radica en el término\(∂Φ_E/∂t\), que hemos ignorado. Con la superficie 1, el electrón cruza la superficie en el tiempo\(δt\), causando una corriente\(I = e/δt\) pero también provocando un cambio en el flux de\(Φ_E ≈ 2πke\) a\(Φ_E ≈ -2πke\). El resultado es que el lado derecho de la ecuación es casi cero. Con superficie 2,\(I = 0\) y\(∂Φ_E/∂t ≈ 0\), así el lado derecho vuelve a ser casi cero.

Cuando se eliminan las aproximaciones utilizadas anteriormente, las ecuaciones de Maxwell predicen un campo que no se desvanece, que es la onda electromagnética esperada que se propaga lejos del electrón a la velocidad adecuada\(c\).

Invarianza de Lorentz

El ejemplo\(\PageIndex{1}\) puede parecer una “historia justamente”, pero la resolución aparentemente milagrosa no es una coincidencia. Sucede porque las ecuaciones de Maxwell son de hecho invariantes bajo una transformación de Lorentz, aunque eso no es obvio cuando están escritas en la forma que se muestra arriba. Hay varias formas de mostrar esto:

• Einstein lo hizo por fuerza bruta en su trabajo de 1905 sobre la relatividad, transformando las coordenadas a través de una transformación de Lorentz y los campos como en la sección 10.4.
• Las ecuaciones de Maxwell son básicamente ecuaciones de onda. (Tienen tanto soluciones de onda como soluciones estáticas). Podemos verificar que cuando iniciamos con una onda plana sinusoidal en una trama, luego transformamos en otra trama, el resultado es nuevamente una solución válida de onda sinusoidal, habiéndose sometido a un desplazamiento Doppler (sección 3.2) y aberración (sección 6.5). Esto requiere comprobar que la onda sigue siendo puramente transversal, pero eso se desprende fácilmente de examinar las invariantes descritas en la sección 10.5. Por un célebre resultado matemático llamado teorema de Fourier, cualquier onda de buen comportamiento puede escribirse como una suma de ondas sinusoidales, y por lo tanto cualquier solución de onda de las ecuaciones de Maxwell en un cuadro también es una solución en cualquier otro marco.
• Las ecuaciones de Maxwell se pueden reescribir en términos de tensores, obedeciendo todas las reglas gramaticales de la gimnasia índice. Si se pueden escribir en esta forma, automáticamente son Lorentz invariantes.

El último enfoque es el más general y elegante, por lo que proporcionaremos un breve boceto de cómo funciona. Ecuación\(\PageIndex{1}\) tiene\(4\pi\) veces la carga a la derecha, mientras que tiene\(4\pi\) veces la corriente. Ambos se relacionan con los cuatro vectores actuales\(\vec{J}\), por lo que claramente necesitamos combinarlos de alguna manera en una sola ecuación con\(\vec{J}\) a la derecha. Dado que la forma local de ecuación implica la divergencia tridimensional, que contiene primeras derivadas, el lado izquierdo de esta ecuación combinada debe tener una primera derivada en ella. Dadas las reglas gramaticales de los tensores y la gimnasia indexada, no tenemos muchas formas posibles de lograrlo. Lo único obvio que hay que probar es

\[\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu} = 4\pi k J^\mu\]

Escribiendo esto por\(\mu\) ser la coordenada de tiempo, obtenemos una relación que equipara la divergencia de\(\vec{E}\) a\(4\pi\) veces la densidad de carga; este es el equivalente local de Ecuación\(\PageIndex{1}\). Si has tomado cálculo vectorial y conoces el operador curl y el teorema de Stokes, entonces puedes verificar eso para\(\mu\) referirte a\(x\),\(y\), y\(z\), recuperamos la forma local de Ecuación\(\PageIndex{4}\). La forma tensorial de expresar Ecuación\(\PageIndex{2}\) y Ecuación\(\PageIndex{3}\) resulta ser

\[\frac{\partial \mathcal{F} ^{\mu\nu}}{\partial x^\lambda} + \frac{\partial \mathcal{F} ^{\nu\lambda}}{\partial x^\mu} + \frac{\partial \mathcal{F} ^{\lambda\mu}}{\partial x^\nu} = 0\]

Ejemplo\(\PageIndex{2}\): A generator

Figura\(\PageIndex{3}\): Un generador crudo, poco práctico.

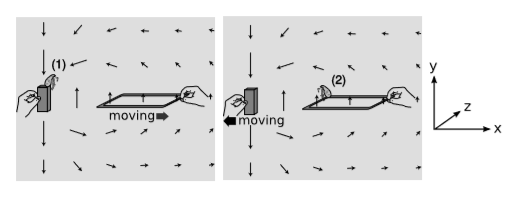
La figura\(\PageIndex{3}\) muestra un generador crudo, poco práctico, representado en dos marcos de referencia.

La pulga 1 está sentada encima de la barra magnética, lo que crea el patrón de campo magnético que se muestra con las flechas. Para ella, el imán de barra obviamente está en reposo, y este patrón de campo magnético es estático. A medida que el bucle de alambre cuadrado es arrastrado lejos de ella y del imán, sus protones experimentan una fuerza en la\(z\) dirección −, según lo determinado por la ley de fuerza de Lorentz\(\vec{F} = q\vec{v} × \vec{B}\). Los electrones, que están cargados negativamente, sienten una fuerza en la\(+z\) dirección. Los electrones de conducción son libres de moverse, pero los protones no lo son En los lados frontal y posterior del bucle, esta fuerza es perpendicular al cable. En los lados derecho e izquierdo, sin embargo, los electrones son libres para responder a la fuerza. Dado que el campo magnético es más débil en el lado derecho, la corriente circula alrededor del bucle.

Pulga 2 está sentada en el bucle, que considera que está en reposo. En su marco de referencia, es el imán de barra el que se mueve. Al igual que la flea 1, observa una corriente circulando alrededor del bucle, pero a diferencia de la flea 1, no puede usar fuerzas magnéticas para explicar esta corriente. En lo que a ella respecta, los electrones estaban inicialmente en reposo. Las fuerzas magnéticas son fuerzas entre cargas móviles y otras cargas móviles, por lo que un campo magnético nunca puede acelerar una partícula cargada comenzando desde el reposo. Una fuerza que acelera una carga desde el reposo sólo puede ser una fuerza eléctrica, por lo que se ve obligada a concluir que hay un campo eléctrico en su región del espacio. Este campo impulsa electrones alrededor y alrededor en círculos — es un campo rizado. ¿Qué razón puede ofrecer el flea 2 para la existencia de este patrón de campo eléctrico? Bueno, ha estado notando que el campo magnético en su región del espacio ha ido cambiando, posiblemente porque ese imán de barra de ahí se ha ido alejando más. Observa que un campo magnético cambiante crea un campo eléctrico rizado. Por lo tanto, el\(∂Φ_B/∂t\) término en la ecuación (\(\PageIndex{3}\)) no es opcional; se requiere que exista si las ecuaciones de Maxwell han de ser igualmente válidas en todos los fotogramas.

Einstein abre su artículo de 1905 sobre la relatividad ¹ comienza con esta frase: “Se sabe que la electrodinámica de Maxwell —como se entiende habitualmente en la actualidad— cuando se aplica a cuerpos en movimiento, conduce a asimetrías que no parecen ser inherentes a los fenómenos”. Luego da esencialmente este ejemplo. Si bien los observadores en los fotogramas 1 y 2 coinciden en todas las mediciones físicas, sus explicaciones de los mecanismos físicos, redactados en el lenguaje de las ecuaciones de Maxwell en la forma, son completamente diferentes. En lenguaje relativista, la explicación de flea 2 se puede escribir en términos de ecuación\(\PageIndex{9}\), en el caso de que los índices estén\(x\)\(z\), y\(t\):

\[\frac{\partial \mathcal{F} ^{xz}}{\partial t} + \frac{\partial \mathcal{F} ^{zt}}{\partial x} + \frac{\partial \mathcal{F} ^{tx}}{\partial z} = 0\]

que es lo mismo que

\[\frac{\partial B_y}{\partial t} + \frac{\partial E_z}{\partial x} + \frac{\partial E_x}{\partial z} = 0\]

Debido a que el primer término es negativo, el segundo término debe ser positivo. Dado que las ecuaciones\(\PageIndex{8}\) y\(\PageIndex{9}\) están escritas en términos de tensores, obedeciendo las reglas gramaticales de la gimnasia índice, se nos garantiza que dan predicciones consistentes en todos los marcos de referencia.

Ejemplo\(\PageIndex{3}\): Conservation of charge and energy-momentum

Resolviendo la ecuación\(\PageIndex{8}\) para el vector actual, tenemos

\[J^\mu = \frac{1}{4\pi k }\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu}\]

La conservación de la carga (sección 9.1) puede expresarse como

\[\frac{\partial J^\mu }{\partial x^\mu} = 0\]

Si sustituimos la primera ecuación por la segunda, obtenemos

\[\frac{\partial }{\partial x^\mu} \left ( \frac{1}{4\pi k }\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu} \right ) = 0\]

o

\[\frac{\partial^2 \mathcal{F}^{\mu\nu}}{\partial x^\mu \partial x^\nu} = 0\]

con una suma sobre ambos\(µ\) y\(ν\). Pero esta ecuación se satisface automáticamente porque\(\mathcal{F}\) es antisimétrica, por lo que para cada combinación de índices\(µ\) y\(ν\), el término que implica\(\mathcal{F}^{µν}\) se cancela por uno que contiene\(\mathcal{F}^{νµ} = -\mathcal{F}^{µν}\). Por lo tanto, la conservación de la carga no tiene que agregarse como condición suplementaria además de las ecuaciones de Maxwell; automáticamente está implícita en las ecuaciones de Maxwell.

Referencias

¹ “Zur Elektrodynamik bewegter K orper”, Annalen der Physik. 17 (1905) 891. Traducción de Perrett y Jeffery

Colaborador

• Template:ContribSRCrowell